На тело, совершающее свободные колебания, действуют две силы:
1. Сила, определяемая по второму закону Ньютона:

где m – масса тела;
а – ускорение;
х – смещение;
t – время.
2. Сила упругости, выраженная по закону Гука:

где k – коэффициент упругости. Знак минус показывает, что сила упругости Fупр всегда направлена в сторону положения равновесия.
На основании второго закона Ньютона (произведение массы тела на его ускорение равно сумме всех действующих сил) получаем:
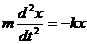 .
.
Перенесем – kx в левую часть равенства, получим:
 .
.
Тогда:

Введем замену:  ,
,
где ω0 – круговая (циклическая) частота колебаний (ω0=2πν)

Получили дифференциальное уравнение второго порядка относительно смещения х.
Решением этого уравнения будет:

или (см. рис.1 и рис. 2).
 ,
,
где А – амплитуда колебания;
φ0 – начальная фаза;
ω0 t+φ0 – фаза колебания в момент времени t;
ω0 t= ∆φ – изменение фазы колебания за время t.
Выведем уравнения мгновенной скорости и мгновенного ускорения, если колебания совершаются по закону косинуса.

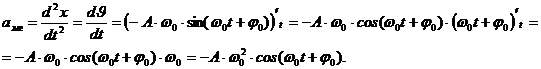
Затухающие колебания.
Все реальные гармонические колебания происходят при воздействии сил сопротивления, на преодоление которых тело затрачивает часть своей энергии, в результате амплитуда колебания уменьшается со временем, т.е. колебания носят затухающий характер.
Представим график затухающего колебания:

Вывод дифференциального уравнения затухающего колебания. На тело, кроме силы  силы упругости
силы упругости  действует сила сопротивления:
действует сила сопротивления:

где r – коэффициент сопротивления.
Согласно второму закону Ньютона можно записать:

или
 .
.
Разделим на массу m, получим:
 .
.
Введем обозначения: 
 ,
,
где β – коэффициент затухания.
Получили дифференциальное уравнение затухающего колебания:
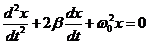 .
.
Решение уравнения существенно зависит от знака разности  ,
,
где ω - круговая частота затухающих колебаний, ω0 - круговая частота собственных колебаний системы (без затухания).
При ω>0 решение дифференциального уравнения будет следующим:
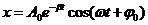 .
.
Амплитуда затухающего колебания в любой момент времени t определяется равенством:
 ,
,
где А0 – начальная амплитуда, указанная на графике (см. рис 3).
Период Т затухающих колебаний определяется по формуле:
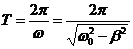 .
.
Скорость затухания (быстрота уменьшения амплитуды) определяется величиной коэффициента затухания β: чем больше β, тем быстрее уменьшается амплитуда.
Для характеристики скорости затухания ввели понятие декремента затухания.
Декрементом затухания называется отношение двух соседних амплитуд, разделенных периодом: 
На практике степень затухания характеризуется логарифмическим декрементом затухания λ, равным:
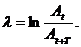
Выведем формулу, связывающую логарифмический декремент затухания λ с коэффициентом затухания β и периодом колебания Т.
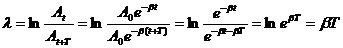
Следовательно:
 .
.
Выведем размерность коэффициента затухания
 .
.
Вынужденные колебания. Вынужденными колебаниями называются колебания, возникающие в системе при воздействии на неё внешней силы, изменяющейся по периодическому закону.
Пусть на систему действует сила:

где F0 – максимальное значение,
ω - круговая частота колебаний внешней силы.
На систему действуют сила  сила сопротивления
сила сопротивления  и сила упругости
и сила упругости  .
.
С учетом всех четырех сил на основании второго закона Ньютона запишем:

или
 .
.
Разделим обе части равенства на m, получим:
 .
.
Введем обозначения:



Получили дифференциальное уравнение вынужденного колебания:
 .
.
Представим график вынужденных колебаний:
 |
В начале амплитуда колебаний возрастает, а затем становится постоянной А.
Для установившихся вынужденных колебаний:

где
 (см. рис. 4)
(см. рис. 4)
Резонанс. Если ω0 и β для системы заданы, то амплитуда А вынужденных колебаний имеет максимальное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Достижение максимальной амплитуды вынужденных колебаний для заданных ω0 и β называется резонансом.
Резонансная круговая частота определяется формулой:

а резонансная амплитуда:
 .
.
Если отсутствует сопротивление (β=0), то амплитуда неограниченно возрастает.
Представим на графиках зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы ω при различных значениях коэффициента затухания:
 |
По виду резонансной кривой резонанс может быть острым при β→0, тупым – при β→1. (см. рис. 5).
По механизму возбуждения резонанс классифицируется на:
- механический; акустический; электромагнитный; парамагнитный; ядерномагнитный.
Возникновение резонансных явлений в организме может быть как полезным, так и вредным. Например, на акустическом резонансе основано восприятия звука, инфразвук может вызвать разрыв тканей внутренних органов.
Автоколебания. При затухающих колебаниях энергия системы расходуется на преодоление сопротивления среды. Если восполнять эту потерю энергии, то колебания станут незатухающими. Пополнять эту потерянную системой энергию можно за счет источника энергии извне, а можно сделать так, чтобы колеблющаяся система сама бы управляла внешним воздействием.
Незатухающие колебания, возникающие в системе за счет источника энергии, не обладающего колебательными свойствами, называются автоколебаниями, а сами системы – автоколебательными.
Классическим примером автоколебаний являются часы: заведенная пружина; поднятая гиря – источник энергии; анкер – регулятор поступления энергии от источника; маятник или баланс – колебательная система.
Амплитуда и частота автоколебаний зависят от свойств самой автоколебательной системы.
Автоколебания осуществляется по следующей схеме:
 |
Через канал обратной связи регулятор, получив информацию о состоянии колебательной системы, осуществляет регулирующую подачи энергии от источника к системе.
К автоколебательным системам относятся сердце, легкие и т.д.
Автоколебательная система сердца может быть представлена в следующем виде:
 |
Порядок выполнения работы:
- Включить кимограф, записать положение равновесия.
- Отклонив маятник в сторону, отпустить его, одновременно включив секундомер.
- После записи последнего n-го колебания отключить секундомер.
- После последнего колебания зарегистрировать положение равновесия и отключить кимограф.
- Записать графики 3-го – 5-го колебательных процессов.
- С помощью линейки для каждого графика определить величину начальной амплитуды (А0) и последней амплитуды (Аn).
- Подсчитать число полных колебаний на графике (n).
- Определить период колебания T:
 где t – время по секундомеру.
где t – время по секундомеру.
- Определить величину коэффициента затухания по формуле:
 .
.
- Определить величину логарифмического декремента затухания:
 .
. - Полученные данные занести в таблицу.
| п/п | А0 (см) | Аn (см) | n | t(c) | T(c) | β(c-1) | λ |
Контрольные вопросы
- Определения и единицы измерения основных характеристик колебательного движения.
- Гармонические колебания. Вывод дифференциального уравнения гармонического колебания и его решение.
- Затухающие колебания. Вывод дифференциального уравнения затухающего колебания и его решение.
- Декремент затухания, логарифмический декремент затухания. Вывод формулы, связывающей логарифмический декремент с периодом колебания и коэффициентом затухания.
- Вынужденные колебания. Дифференциальное уравнение вынужденного колебания и его решение.
- Резонанс и его значение в медицине.
- Автоколебания.
Тестовые задания
- Циклической (круговой) частотой называется число полных колебаний за:
а) 1 с; б) 1 мин; в) 1 ч; г) 2π с.
- Укажите формулу, связывающую циклическую частоту ω с частотой ν:
а)  ; в)
; в)  ;
;
б) 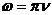 ; г)
; г)  .
.
- Укажите формулу, по которой определяется амплитуда затухающего колебания в любой момент времени t:
а)  ; в)
; в)  ;
;
б)  . г)
. г)  .
.
- Декрементом затухания называется отношение:
а) двух соседних амплитуд;
б) двух соседних амплитуд, разделенных периодом;
в) первой и последней амплитуд;
г) двух амплитуд, разделенных полупериодом.
- Укажите единицу измерения коэффициента затухания β:
а) с; в) с-1;
б) безразмерная величина; г)  .
.
6. Укажите решение дифференциального уравнения свободного гармонического колебания:
а)  ; в)
; в)  ;
;
б) 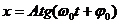 ; г)
; г)  .
.
7. Укажите, сколько сил действует на систему, если она совершает свободные гармонические колебания:
а) одна; в) три;
б) две; г) четыре.
8. Укажите дифференциальное уравнение свободного гармонического колебания:
а)  ; в)
; в)  ;
;
б)  ; г)
; г) 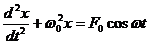 .
.
9. Укажите решение дифференциального уравнения затухающего колебания:
а) 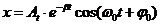 ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
10. Сколько полных колебаний тело должно совершить в одну минуту, чтобы частота его колебаний равнялась 1 Гц:
а) 1; в) 120;
б) 60; г) 30;
11. Укажите подстановку в уравнение смещения затухающего колебания:
 :
:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  ;
;
12. Укажите, сколько сил действует на систему, если она совершает вынужденные колебания:
а) две; в) четыре;
б) три; г) пять.
13. Укажите дифференциальное уравнение вынужденного колебания:
а)  ; в)
; в)  ;
;
б) 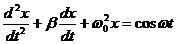 ; г)
; г)  .
.
14. Укажите блок – схему, по которой осуществляются автоколебания:
 |
15. Укажите формулу, связывающую логарифмический декремент затухания λ с периодом колебания Т и коэффициентом затухания β:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
16. Укажите дифференциальное уравнение затухающего колебания:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
17. Укажите, по какой формуле определяется период колебания Т, если за время t тело совершило n полных колебаний:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  .
.
18. Укажите единицу измерения логарифмического декремента затухания:
а) с-1; в) с;
б) с2; г) безразмерная величина.
19. Укажите, какой параметр в уравнении смещения  указывает на то, что процесс носит затухающий характер:
указывает на то, что процесс носит затухающий характер:
a) t; б) ω0; в) А0; г) β.
20. Укажите, какая сила вызывает уменьшение амплитуды при затухающих колебаниях:
а) ускоряющая сила;
б) сила упругости;
в) сила сопротивления;
г) сила давления.
21. Укажите, при каком значении декремента затухания процесс затухания будет проходить наиболее медленно:
а)  ; в)
; в) 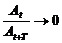 ;
;
б)  ; г)
; г)  .
.
 22. Укажите, на каком из графиков показан период колебания Т:
22. Укажите, на каком из графиков показан период колебания Т:
|
23. Укажите график вынужденного колебания:
 |
24. Укажите, каков физический смысл знака «-» в формуле закона Гука 
а) физический смысл отсутствует;
б) показывает, что направления силы упругости Fупр и смещения х совпадают;
в) показывает, что направления силы упругости Fупр и смещения х противоположны;
г) показывает, что направления силы упругости Fупр и смещения х взаимно перпендикулярны.
25. Частотой колебания ν называется величина, показывающая число полных колебаний:
а) за минуту; в) за час;
б) за секунду; г) за сутки.
26. Укажите, в каких единицах измеряется циклическая частота ω:
а) в секундах; в) в минутах;
б) в Гц ; г) в часах.
27. Укажите условие резонанса при β=0:
а) ωрез>ω0; в) ωрез≠ω0;
б) ωрез=ω0; г) ωрез<ω0.
28. Укажите уравнение скорости незатухающего колебания, совершаемого по закону:
 :
:
а)  ; в)
; в) 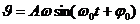 ;
;
б)  ; г)
; г)  .
.
29. Укажите уравнение ускорения незатухающего колебания, совершаемого по закону:
 :
:
а)  ; в)
; в)  ;
;
б)  ; г)
; г)  ;
;
30. Укажите, что в автоколебательной системе сердца выполняет роль регулятора:
а) метаболические процессы;
б) сердце;
в) сино – атриальный узел;
г) ряд внутрисердечных рефлекторных дуг и рефлекторные дуги ЦНС.
31. Укажите, функцию какого параметра выполняет f0 в дифференциальном уравнении вынужденного колебания  :
:
а) скорости; в) массы;
б) ускорения; г) внешней силы.
32. Укажите, функцию чего в классическом примере автоколебаний в часах выполняет анкер:
а) источника энергии; в) клапана (регулятора);
б) колебательной системы; г) обратной связи.
33. Укажите уравнение, по которому определяется амплитуда А установившегося вынужденного колебания:
а)  ;
;
б)  ;
;
в) 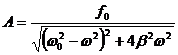 ;
;
г)  .
.
34. Чему будет равен логарифмический декремент λ, если отношение амплитуд А t и At+ T равно 2,7:
а) λ =1; в) λ =3;
б) λ =2; г) λ =4.
35. Чему будет равно отношение амплитуд А t и At+ T, если логарифмический декремент λ равен 1,1:
а) 1; б) 2; в) 3; г) 4.
Лабораторная работа №2
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО
НАТЯЖЕНИЯ ЖИДКОСТЕЙ
Цель работы. Изучение явления поверхностного натяжения. Освоение методик определения коэффициента поверхностного натяжения жидкости.
Актуальность. Коэффициент поверхностного натяжения жидких сред организма представляет диагностический и научно-исследовательский интерес, а также позволяет студентам понять сущность капиллярных явлений и газовой эмболии.
Приборы и принадлежности: штатив, лабораторные весы, разновесы, кольцо, сосуд с исследуемой жидкостью, песок, штангенциркуль, сталагмометр, исследуемая и эталонная жидкости.
Теоретическая часть
Поверхностное натяжение. Характерным свойством жидкостей является поверхностное натяжение, образующееся на свободной поверхности жидкости, т.е. на границе с газообразной средой (а также на границе с другой несмачивающейся жидкостью или несмачиваемым твердым телом).
Поверхностное натяжение обусловлено силами притяжения между молекулами. В сосуде, заполненном жидкостью, выделим две молекулы (А и В), рис. 1.
 |
Результирующая всех сил, действующих на молекулу В, равна нулю. На молекулу А, находящуюся на свободной поверхности жидкости, силы притяжения со стороны окружающих молекул жидкости действуют значительно сильнее, чем со стороны паров жидкости или газа, с которым жидкость граничит, последним можно пренебречь.


Каждую из сил, действующих на молекулу А со стороны жидкости, можно разложить на две составляющие, которые направлены: 1) по касательной к поверхности жидкости, 2) перпендикулярно первой. Складывая между собой перпендикулярные составляющие, получают силу fn, направленную вглубь массы жидкости. Касательные образуют равные и противоположные силы fk, направленные вдоль поверхности жидкости (рис. 2). Силы fn всех молекул поверхностного слоя, складываясь, оказывают на жидкость давление, которое вызывает сближение молекул и уравновешиваются силами их отталкивания. Это давление называется внутренним, или молекулярным, давлением жидкости.
Силы fk, взаимно уравновешиваясь по отношению к каждой молекуле, в то же время связывают их между собой дополнительными силами притяжения (подобно тому, как это имеет место между молекулами в растянутой упругой пленке). Суммарное действие этих сил и называют силой поверхностного натяжения Fn. Эта сила приложена к контуру, ограничивающему поверхность жидкости. Сила поверхностного натяжения в каждой точке контура направлена касательно к поверхности жидкости и перпендикулярно линии её контура, так, чтобы сократить свою свободную поверхность.
Для смачивающих жидкостей эта сила уравновешивается равной ей по величине и противоположной по направлению силой  сцепления молекул жидкости и вещества стенок сосуда, которые ограничивают свободную поверхность жидкости (рис 3).
сцепления молекул жидкости и вещества стенок сосуда, которые ограничивают свободную поверхность жидкости (рис 3).
Поверхностное натяжение характеризуется коэффициентом поверхностного натяжения, который численно равен силе поверхностного натяжения Fn, приходящейся на единицу длины контура l, ограничивающего поверхность жидкости:
 .
.
Коэффициент поверхностного натяжения зависит от природы жидкости и от температуры (уменьшается при её повышении), но не зависит от величины и формы поверхности. Единицы измерения коэффициента поверхностного натяжения в системе СИ (Н\м), в системе СГС (дин\см).
Для того, чтобы переместить молекулу из глубины жидкости в поверхностный слой, надо совершить работу против равнодействующей молекулярных сил, направленной вглубь жидкости. Эта работа идет на увеличение потенциальной энергии молекулы. Следовательно, молекулы поверхностного слоя жидкости имеют дополнительную внутреннюю энергию, называемую потенциальной энергией. Соотношение поверхностной энергии Wn и коэффициента поверхностного натяжения жидкости выражается следующей формулой:
 ,
,
т.е. коэффициент поверхностного натяжения равняется поверхностной энергии Wn, приходящейся на единицу площади S свободной поверхности жидкости. В этом случае коэффициент поверхностного натяжения измеряется в СИ –  , в системе СГС –
, в системе СГС –  .
.
В таблице представлены коэффициенты поверхностного натяжения некоторых жидкостей.
| Жидкость | σ, Н\м |
| Вода Желчь Молоко Моча Ртуть Спирт Сыворотка крови Эфир | 0,0725 0,048 0,05 0,066 0,47 0,022 0,06 0,017 |
Снижения поверхностного натяжения можно достигнуть введением в жидкость поверхностно–активных веществ, уменьшающих энергию поверхностного слоя. Поверхностно–активные вещества имеют большое значение в биологических процессах, особенно на клеточном и молекулярном уровнях (речь идет о поверхностях раздела различных сред). Поверхностно–активные вещества содержатся во многих жидких средах организма.
Величина коэффициента поверхностного натяжения имеет диагностическое значение в клинике. Например: появление в моче желчных пигментов приводит к резкому снижению σ, до 0,056 
Капиллярные явления. Между молекулами стенок сосуда и молекулами поверхности жидкости действуют силы притяжения (адгезии) Fа (Адгезия – это прилипание молекул двух различных тел, вызванное взаимным притяжением. Когезия – это сцепление молекул одного тела между собой, вызванное взаимным притяжением), что приводит к возникновению краевого угла α между стенками сосуда и поверхностью жидкости. Равнодействующая сил когезии и адгезии всегда перпендикулярна поверхности жидкости.

Если α<90° – жидкость смачивает стенку, поверхность жидкости имеет вогнутую форму, называемую вогнутым мениском (рис. 4).
Если α>90°, то жидкость не смачивает стенку. Поверхность жидкости имеет выпуклую форму, называемую выпуклым мениском (рис.5).
Под действием сил поверхностного натяжения поверхностный слой жидкости искривлен и оказывает дополнительное давление по отношению к внешнему давлению. Результирующая сил поверхностного натяжения искривленной поверхности направлена в сторону вогнутости (к центру кривизны). В случае сферический поверхности, радиус кривизны которой r, дополнительное давление определяется по формуле Лапласа:
 .
.
Явление поднятия или опускания уровня жидкости в узких трубках в связи с действием дополнительного давления называется капиллярностью.
 Рассмотрим вогнутый мениск (рис 6). Равновесное состояние, показанное на рисунке, наступает тогда, когда давление ρgh уравновесит ∆Р. Из рисунка видно, что радиус мениска будет:
Рассмотрим вогнутый мениск (рис 6). Равновесное состояние, показанное на рисунке, наступает тогда, когда давление ρgh уравновесит ∆Р. Из рисунка видно, что радиус мениска будет:

где R – радиус капилляра.
Учитывая формулу Лапласа, имеем:
 .
.
Тогда высота поднятия жидкости в капилляре будет
 ,
,
причем она зависит от свойств жидкости и материала капилляра, а также от его радиуса.
Капиллярные явления имеют большое значение для жизни растений, т.к. способствуют поднятию воды и питательных растворов из почвы вдоль ствола растения. Капиллярными свойствами обладает всякое пористое тело, например, фильтровальная бумага, сухой мел и.т.д. Пористые тела легко пропитываются смачивающими жидкостями и удерживают их. Наоборот, для несмачивающих жидкостей эти тела являются непроницаемыми.
Газовая эмболия. Пузырек газа, попавший в смачивающую жидкость, протекающую по узкой трубке, ограничен с обеих сторон менисками, под которыми образуется добавочное давление.
 Если жидкость неподвижна, мениски имеют одинаковый радиус (r1= r2) и добавочные давления под ними взаимно уравновешиваются. Силы добавочного давления: F1= F2 (рис. 7а).
Если жидкость неподвижна, мениски имеют одинаковый радиус (r1= r2) и добавочные давления под ними взаимно уравновешиваются. Силы добавочного давления: F1= F2 (рис. 7а).
Если на жидкость действует внешнее давление Р, то мениски, удерживаемые силами адгезии, будут
деформироваться и радиусы их изменяются: r1> r2 (рис. 7б). Добавочные давления под ними уже не будут уравновешиваться и создадут разность давлений ∆Р, противодействующую давлению Р и затрудняющую движение жидкости. Если пузырьков много, то может произойти полная закупорка трубки.
Наибольшее сопротивление движению жидкости оказывают мениски пузырька, образовавшегося у разветвления трубки, так как в этом случае с одной стороны вместо одного мениска образуются два с меньшими радиусами кривизны (рис. 7в).
Такие явления могут происходить в кровеносной системе человека. Попавшие в кровь пузырьки воздуха могут закупорить мелкий сосуд и лишить кровоснабжения какой-либо орган. Это явление, называемое эмболией, может привести к серьезному функциональному расстройству или даже летальному исходу. Так, воздушная эмболия может возникнуть при ранении крупных вен: проникший в ток крови воздух образует воздушный пузырь, препятствующий прохождению крови. Пузырьки воздуха не должны попадать в вены при внутривенных вливаниях.
Газовые пузырьки в крови могут появиться у водолазов при быстром подъеме с большой глубины на поверхность, у летчиков и космонавтов при разгерметизации кабины или скафандра на большой высоте (газовая эмболия). Это обусловлено переходом газов крови из растворенного состояния в свободное (газообразное) в результате понижения окружающего атмосферного давления. Ведущая роль в образовании газовых пузырьков при уменьшении давления принадлежит азоту, так как он обусловливает основную часть общего давления газов в крови и не участвует в газообмене организма и окружающего воздуха.
Практическая часть
 Упражнение №1. Определение коэффициента поверхностного натяжения воды методом отрыва кольца.
Упражнение №1. Определение коэффициента поверхностного натяжения воды методом отрыва кольца.
Пусть кольцо, имеющее:
d1 – внешний диаметр,
d2 – внутренний диаметр,
h – толщина кольца,
отрывается от поверхности воды.
Коэффициент поверхностного натяжения исследуемой
жидкости определяем по формуле:
 , (1)
, (1)
|
l – длина контура отрыва кольца от поверхности жидкости,
равная сумме длины внешней и внутренней окружности кольца:
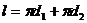 ; (2)
; (2)
внутренний диаметр кольца  подставляем в формулу (2), тогда
подставляем в формулу (2), тогда
 . (3)
. (3)
Подставляем длину контура отрыва кольца (l) в формулу (1):

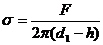
Порядок выполнения работы
1. Выставить кольцо строго горизонтально.
2. С помощью песка уравновесить весы.
3. Подвести сосуд с исследуемой жидкостью (вода) под кольцо и привести кольцо в соприкосновение с поверхностью жидкости.
4. На чашку весов малыми порциями подсыпается песок до тех пор, пока кольцо не оторвется от поверхности воды.
5. Вытереть кольцо и уравновесить весы с помощью разновесов.
6. По формуле второго закона Ньютона найти вес песка Р = mg и приравнять его к силе поверхностного натяжения.
7. Провести этот же эксперимент, используя в качестве исследуемой жидкости воду с добавлением поверхностно-активного вещества (стиральный порошок).
8. Данные занести в таблицу.
| № п/п | d 1 (м) | h (м) | m (кг) | Р= F пн (Н) | σ 
| Δσ 
| (Δσ)2

| m 
| t (0,95; n-1) | Доверитель ный интервал (Н/м) |  100% 100%
|
| 1. | |||||||||||
| 2. | |||||||||||
| 3. | |||||||||||

| 
| Д |
Упражнение №2. Определение коэффициента поверхностного натяжения
методом отрыва капель.

В медицинской практике прибор, с помощью которого указанным методом определяется коэффициент поверхностного натяжения, называется сталагмометром. Он представляет капилляр, который в одном месте расширен. Это расширение представляет собой рабочий объем прибора, ограниченный сверху и снизу рисками. Работа со сталагмометром сводится к подсчету капель, вытекающих из рабочего объема. Для увеличения точности метода проводится сравнительный анализ измерения коэффициента поверхностного натяжения исследуемой жидкости по сравнению с коэффициентом эталонной жидкости. В качестве эталонной жидкости берется дистиллированная вода.
Вывод рабочей формулы






