Nbsp; Восточная (западная) модель

H₃ Ì H₆ Ì H₁₂ Ì H₃₆

H₃ Ì H₆ Ì H₁₂ Ì H₁₂₀

H₃ Ì H₆ Ì H₁₈ Ì H₃₆

H₄ Ì H₈ Ì H₁₆ Ì H₄₈

H₄ Ì H₁₂ Ì H₃₆

H₄ Ì H₁₂ Ì H₄₈

H₆ Ì H₁₂ Ì H₃₆

H₆ Ì H₁₂ Ì H₁₂₀

H₆ Ì H₁₂ Ì H₄₈

H₆ Ì H₁₈ Ì H₃₆

H₆ Ì H₂₄ Ì H₄₈

H₆ Ì H₂₄ Ì H₁₂₀

Так в представленном 6-вершинном графе отсутствует ребро 1-2, отображающее эффективную сельскохозяйственную интеграцию (животноводства и зерноводства), но присутствует ребро 3-4, воплощающее коллективистскую взаимопомощь в суровых природных условиях России. А далее на таком графе строится последовательность вложенных подгрупп.

К другим эволюционным возможностям приводит исходный граф для индейцев Северной Америки: здесь также отсутствует эффективная сельскохозяйственная интеграция, но кроме того отсутствуют и социальные свойства, воплощаемые ребром 3-4.

Nbsp; Северо-Американская модель

H₄ Ì H₁₂ Ì H₃₆

H₄ Ì H₁₂ Ì H₄₈

H₄ Ì H₈ Ì H₁₆ Ì H₄₈

 

На основе подхода, развитого в работах[1-5], строятся пос­ледовательности вложенных подгрупп, отображающие в опреде­ленном смысле оптимальные эволюционные траектории системы общественного воспроизводства, начиная с архаичного времени.

 

3. Мера сложности, ее задание и примеры расчета

Мера сложности

Теперь, когда мы ввели понятие эволюционных цепочек подгрупп, можно вернуться к отправной точке нашего рассуждения. Исходя из того, что нам известно положение общества в текущий момент эволюции, т.е. нам известна группа перестановок, в которых циклирует система ЯВ, мы можем определить возможные пути эволюции общества, строя цепочки подгрупп (подполугрупп) над указанной исходной группой (полугруппой). Естественным образом возникает несколько вопросов. Например, по какому же пути пойдет развитие общества, если альтернатив несколько? Как нам известно: любой эволюционный переход связан с некоторыми инновациями, нововведениями, включающими в том числе и "правила запрета". Сами же инновации связаны с текущим уровнем развития общества, или, как мы будем говорить далее – сложностью СОВ. Таким образом, возникает еще один вопрос: как определить сложность СОВ? Нами был выбран подход, связанный с заданием сложности как меры на множестве групп перестановок.

Когда мера определена, мы можем вычислить ее для каждой подгруппы из полученных цепочек подгрупп. Далее, рассматривая разность[5] мер соседних подгрупп, можем судить о возможности дальнейшей эволюции сообществ. Отдельно стоит отметить ситуацию, когда сложность эволюционного перехода велика, в таком случае можно говорить об эволюционном тупике в развитие общества. Эволюционный тупик – это невозможность перейти с одной ступени развития на следующую ступень, в силу большого разрыва между ними. Это можно интерпретировать, как невозможность примитивной социальной системы трансформироваться в значительно более развитую. Обязательно должны быть некоторые промежуточные стадии (периоды) развития, отображенные промежуточными группами на соответствующем графе.

Перейдем теперь непосредственно к введению меры сложности.

Задание меры сложности

Рассмотрим некоторую группу перестановок 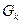, где k – порядок группы. Нам необходимо ввести меру сложности H().

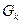Положим, что сложность группы равна сумме сложностей каждой перестановки из этой группы:

.

Для вывода оценки сложности перестановки будем использовать предложенный А.И. Уемовым[3] подход для построения выражения для субстратно-структурной сложности систем. В указанном подходе используется понятие энтропии. Напомним, что энтропия вводится как мера неопределенности случайной величины. Если задано конечное множество - значений случайной величины с распределением вероятностей 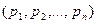, энтропией называется величина:

.

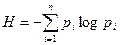При введении меры сложности мы учитывали следующие основные свойства энтропии:

1. ;

2. – принимает минимальное значение равное нулю, если 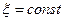, т.е. все значения равны нулю, кроме одного, равного 1;

3. – принимает свое максимальное значение равное , если все .

Запишем перестановку в виде ориентированного графа. Пусть этот граф имеет n вершин. Рассмотрим произвольную вершину графа, которую обозначим символом , где j=[1,n]. Из свойств перестановок будем иметь, что эта вершина либо будет принадлежать циклу, либо в этой вершине будет петля. Теперь запишем типы бинарных отношений, в которые может вступать эта вершина с другими:

1) - нет связи или, по-другому, нет маршрута между парой вершин;

2) - между вершинами существует маршрут длиной один;

…

n) - между вершинами существует маршрут длиной (n-1).

Обозначим символом те отношения , где первым коррелятором является . Каждое из этих отношений имеет определенную экстенсиональную длину на вершине , которую мы обозначим символом . Т.к. каждая вершина может вступать не более чем в (n-1) отношение, то будет выполнено равенство:

.

Вероятность того, что отношение реализуется на вершине , обозначим 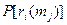. Значение вероятности может быть определено по формуле:

.

Здесь в числителе – фактическая, а в знаменателе – максимально возможная экстенсиональная[6] длина отношения на вершине . При этом, как несложно видеть, выполняются следующие соотношения:

;

.

Таким образом, энтропию, приходящуюся на вершину , можно задать следующей формулой:

.

Суммируя теперь по всем вершинам, получим общую энтропию перестановки:

.

Полученную величину можно рассматривать как меру сложности перестановки. Отметим несколько принципиальных свойств полученной меры и дадим им обоснование с точки зрения социологии:

1. и , где 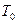- тождественная перестановка. Очевидно, что сложность ВЦ, в котором нет связей между ЯВ, должна быть минимальной.

2. Чем больше средняя длина цикла в графе, тем больше сложность перестановки. Дадим социологическую интерпретацию этого свойства. Мы знаем что, чем больше длина цикла, тем больше ЯВ задействовано в едином обменном цикле. Совершенно очевидно, что ВЦ с максимальным задействованным числом ЯВ в нем, должен иметь большую сложность, т.к. СОВ в этом случае должна иметь больший эволюционный потенциал.

3. При уменьшении средней длины циклов в графе, также уменьшается величина сложности. Это удовлетворяет предположению, что система, разбитая на мелкие не связанные между собой группы ЯВ, имеет меньший эволюционный потенциал (сложность), чем единая система.

4. Отметим важную особенность полученной меры. При изменении числа вершин графа, т.е. при добавлении новых ЯВ, даже без добавления новых ребер будет изменяться величина сложности. Таким образом, при наращивании СОВ новыми ЯВ, перед сравнением сложностей в эволюционной цепи, необходимо делать пересчет сложности для предыдущих подгрупп.

Используя полученное выражение для H(T), мы можем записать меру сложности на группе H(G):

или .

Далее для краткости будем называть значение меры сложности просто «сложностью» или «структурной сложностью».

Примеры расчета сложности

I. Приведем пример расчета сложности для нескольких перестановок, реализуемых в 4-х вершинном графе. Для 4-х вершинного графа возможны следующие четыре типа бинарных отношений между вершинами:

1) - нет связи или, по-другому, нет маршрута между парой вершин;

2) - между вершинами существует маршрут длиной 1;

3) - между вершинами существует маршрут длиной 2;

4) 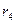- между вершинами существует маршрут длиной 3.

 

1. Перестановка - (134). Подсчитаем экстенсиональные длины отношений:

для 1-й вершины: , , ;

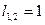для 2-й вершины: ;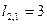

для 3-й вершины: , , ;

для 4-й вершины: , , .

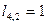Отсюда для сложности получим выражение:

2. Перестановка - (1324). Экстенсиональные длины отношений:

для 1-й вершины: , , ;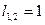

для 2-й вершины: , , ;

для 3-й вершины: , , ;

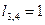для 4-й вершины: , , .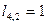

Отсюда получим:

.

 

II. Теперь рассмотрим результат, полученный для двух различных групп четвертого порядка и 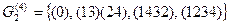. Опуская расчеты, запишем полученные значения сложности:

;

.

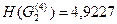Полученный результат полностью оправдывается тем, что вторая группа описывает более «сложный» образ жизни общества, нежели первая. Это видно из более сложных ВЦ второй группы, в циклах которых одновременно задействовано большее количество ЯВ.

III. Наконец, рассмотрим результат расчетов сложности на цепочках вложенных подгрупп. Возьмем две цепочки подгрупп:

Последовательности соответствующих значений сложности будет следующей:

Здесь можно отметить, что переход от группы 2-го порядка к группе 4-го порядка в первой цепочке имеет большую сложность, чем во второй. Это символизирует то, что СОВ отраженной группой , легче совершить переход к группе , чем к группе , т.к. во втором случае обществу необходимо сделать больше число инноваций, способствующих образованию более сложных ВЦ.

На приведенном ниже рисунке изображено основное окно программы после завершения поиска групп 2-го порядка в полном четырех вершинном графе. Для каждой из полученных групп (список справа) имеется возможность сделать ее начальной для следующего поиска, а также просмотреть свойства группы (сложность, порядок, входящие в группу перестановки).

 

 

Под списком найденных подгрупп имеется кнопка, позволяющая графически отображать данные, полученные в результате расчетов:

1.
Если идет построение цепочки групп, то отображается текущая построенная цепочка. На приведенном ниже рисунке изображен пример результатов расчетов программы при построении цепочки групп (эволюция СОВ).

2. Если идет построение решетки групп, то отображается решетка. На приведенном ниже рисунке изображен пример результатов расчетов программы на четырех вершинном графе. В качестве начальной группы здесь использовалась группа второго порядка.

 

 

Также программа реализует поиск в решетке оптимальной эволюционной траектории. Остановимся чуть подобнее на критерии указанного поиска. Нами был выбран следующий критерий: оптимальной траекторией считать ту, на которой максимум разностей сложностей между группами, находящимися на траектории, достигал бы минимума. С социологической точки зрения это обосновывается тем, что разность между эволюционными потенциалами соседних групп показывает сложность перемены общественного уклада в СОВ, и, выбирая минимум среди максимумов, мы тем самым выбираем такую траекторию развития общества, где указанные переходы имеют наименьшую сложность. Этим отражается идея того, что обществу «проще» и безболезненнее развиваться небольшими переменами, нежели резкими (революционными) изменениями внутренних укладов.

В результате в СОВ, характеризующейся полным четырех вершинным графом были получены следующие оптимальные траектории:

1). 3 траектории вида:

2). 4 траектории вида:

Соответствующие значения сложности будут следующими:

1).

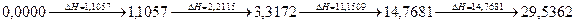
2).

 

Важнейшей проблемой, социологически весьма актуальной, являе­тся проблема привязки последовательности этих под­групп к последовательностям спектров воспроизводственных цик­лов, определяю­щих последовательно усложняющиеся образы жиз­ни.

В качестве основных методов привязки выбраны биолого-генетические методы локализации популяций и физические методы датировки археологических находок.

Общая качественная картина выглядит следующим образом:

В мезолите (10 – 5 тысяч лет до Р.Х.)[7] завершается период отступления ледника, а т.е. и расселения представителей ориньяк­ской и граветтянской культур, двигавшихся вслед за уходящими на север стадами мамонтов как основной кормовой базой первобытных охот­ников. К этому времени в силу сущест­венного сокращения численности мамонтов происходит изменение в пищевом рационе древних людей - все большее место занимает охота на среднюю и мелкую дичь. Отсюда видна потреб­ность в новом охотничьем оружии, и место дротика с копьеметалкой для коллективной охоты на мамонтов начинает занимать лук со стре­лами, позволяющий переходить к автономному обеспечению пи­щей отдельной семьи. К этому времени появляются первые дома­шние животные – была приручена собака. Приведем, следуя [11, стр 41] датировку основных изобретений в период мезолита и конца неолита (начала энеалита):

XIII – X тысяч лет до н.э. – сверление отверстий; строительство шалашей; изготовление простейших саней; обжиг глиняных изделий; появление копьеметалки, лука;

8 тыс. лет до н.э. – появление посуды из глины, первых изделий из меди (Турция, Иран); изобретение вина;

6 тыс. – 5 тыс. лет до н.э. – начало развития земледелия (долины Ефрата, Тигра), хотя доминирующим способом добычи средств к существованию остается охота; появляется жгутовая лепка; жили­щами являются землянки и свайные постройки, т.е. к этому времени уже изобретены лодка и деревянная "баба" для забивки свай;

4 тыс. – 3 тыс. лет до н.э. – поздний неолит и начало энеолита - ис­пользуются орудия земледелия - мотыги, зернотерки, серпы; развива­ют­ся технологии сверления, пиления, шлифования и полирования; ста­но­вится ткачество; появляются сложные орудия; зарож­да­ется и становит­ся скотоводство как отрасль оседлого домашнего хозяй­ства; археологи и историки называют этот этап расцвета родового строя как патриархат.

Нас безусловно интересует не вообще историческая привязка нашего теоретико-графового и теоретико-группового описания древ­них сообществ, а, прежде всего, в интересах модельного отра­жения социальной наследственности в свойствах "Макросоци­ума", привя­зка указанного подхода к историческим данным (археологии, линг­вистики и т.д.) по формированию протославянской общности [10]:

3 тыс. - 2 тыс. лет до н.э. (культура шаровых амфор) - к древнему земледелию прибавилось значительно развившееся скотоводство; по­я­вился колесный транспорт (упряжка волов); происходит овла­де­ние верховым конем; "Очевидно, очень далеко по сравнению с общест­вен­ной нивелированностью зашло социальное развитие внутри племен. Вы­де­лились вожди и воины - всадники; археологам известны погре­бения вождей в больших мегалитических гробницах…" [10, стр 149].

С выделением начальной социальной иерархии в родах и сосед­ских общинах, т.е. формированием института старейшин, у нас связы­ва­ется появление 6-ти вершинных графов и соответствующей группы симметрий октаэдра. Вождь племени - это уже следующий уровень со­ци­альной иерархии, хотя и до сегодняшнего дня в Сибири известны ар­ха­­ичные народности, которые существуют на уровне межродовых отно­шений, и в которых не возникает необходимость в вожде, что и отра­жается в соответствующем типе теоретико-группового рассмотрения.

Однако наиболее удивительным является то, что именно эта теоретико-групповая уникальная основа социального генотипа свя­зана с «основным зако­ном развития любого общества – реализацией откры­тий и изобре­тений», т.е. инноваций, сформулированным впервые еще В.М.Бехтеревым [7]. Связь была установлена в работе [1 - 4] с позиций информационного подхода, который своеобразие ценност­ных ориен­тиров, устоев мировоззренческой позиции, норм и тради­ций, одним словом, духовности данного этноса, народа или нации расценивает как код, фильтрующий разнообразную информа­цию и позволяющий осуще­ст­влять такие открытия и изобретения, которые другим не под силу или даются с большим трудом. Вообще эта закономерность есть проявления известного закона необходимо­го разнообразия, обосновывающего уникальную ценность каждого народа, но как отдельный социальный закон - закон развития общес­тва - был сформулирован в работах [1, 4] как количественный закон предсказания сложности инноваций.

Закон перемен (Бехтерев В.М.)

Эволюция системы ЯВ есть услож­няющийся ряд ее состо­яний при некото­ром циклировании в спектре найденных ВЦ (воспроиз­водственный цикл [8]) жиз­не­деятельности, при­чем столько времени, сколько надо, что­бы, находясь на данном уровне сложности когни­тивных воз­мо­ж­ностей, открыть - изобрести и в широкой общности осво­ить но­вые структурные формы, сохраняя, в том числе, и уже най­де­н­ные.

Сложность пакета осваиваемых иннова­ций пропорциона­льна сложности уровня ВЦ.

Получена оценка – H(n) = ln T_n усложняющегося спектра ВЦ, пропорциональная сложности осуществляемых инноваций, что закла­ды­­вает основу для прогноза сложности предстоящих открытий и изо­бре­тений:

 

ln n! – ln ln n! < H(n) < ln L + ln n! – ln ln n!, (1)