Множество H является подгруппой группы G, если

Портфель изобретений – это общее число изобретений и рационализаторских предложений, предназначенных к внедрению.

Еще раз напомним, что графом G называется любая пара (V,E), где - множество элементов любой природы, а - семейство пар элементов из V, причем допускаются пары вида, называемые петлями. Если пары в V рассматриваются как неупорядоченные, то граф называется неориентированным, если как упорядоченные, то граф называется ориентированным (орграфом).

Элементы множества V называются вершинами графа, а пары из E – его ребрами; в орграфе они называются ориентированными ребрами или дугами.

Взаимно однозначное отображение множества из n элементов на себя будем называть перестановкой.

Группой называется множество A={a₁, a₂,…a_n} с бинарной операцией 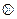на нем такое, что выполняются следующие аксиомы:

1. (аксиома замыкания) для любой произвольной пары a _k, a_l всегда найдется элемент a _r того же множества A={a₁, a₂,…,a_n} такой, что

a_r = a_k 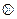a_l

2. (аксиома ассоциативности) Для произвольных элементов r, s, t из группы A:

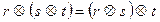
3. (аксиома о единичном элементе) В группе A существует единственный элемент I, такой, что:

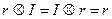
4. (аксиома об обратных элементах) Для любого элемента r из A существует единственный элемент 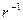из A, такой, что:

.

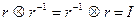Множество H является подгруппой группы G, если

1. каждый элемент множества H является элементом группы G;

2. H есть группа (относительно бинарной операции, определенной в группе G).

Порядок группы равен числу ее элементов. Перестановки образуют группу. Число элементов одной перестановки есть степень этой группы, а число перестановок, образующих группу, есть ее порядок. Так полная группа симметрий тетраэдра есть группа перестановок его вершин, т.е. ее степень равна 4, а порядок равен 4! = 24.

Группа G называется коммутативной группой, если для бинарной операции, определенной в этой группе, выполняется свойство коммутативности: s Ä t = t Ä s.

Начнем с исторически первого воспроизводственного цикла (ВЦ) СОВ - цикла обмена веществ между обществом и природой и введем обозначения:

ВП_i – вещество природы, представленное своей конкретной i - ой формой из некоторого списка;

ВС_j – воспроизводственный субстрат, представленный своей конкретной j - ой формой из некоторого списка.

Для первого ВЦ доисторического времени и Природа, и складывающееся первобытное Общество были еще не субъекты обмена ВП, как это выписывается некоторыми современными экологами, а выступали как объекты взаимодействия (см. Рис.1). При этом следует сразу различать формирующиеся этнические общности по роли суровости этого экологического фактора: одно дело – этносы, возникающие в благодатной зоне действия Гольфстрима, и другое – этносы, постоянно атакуемые джунглями, пустыней или суровыми зимами, землетрясениями и пр. В первом случае – даже одна семья может самодостаточно противостоять осложнениям стихии, относя на свой счет удачные хозяйственные результаты в этих условиях, во втором случае – это возможно только общиной с отложением в памяти именно коллективных успехов.

(Общность семей гуманоидов)₁ (Общность семей гуманоидов)₂

Рис.1 Природная среда₁ Природная среда₂

Обозначим Природные среды цифрами 1 и 3, а Общности семей гуманоидов цифрами 2 и 4. Тогда ситуация на Рис.1 с учетом социальных последствий вышеописанных двух возможностей коэволюции человеческих сообществ с Природой может быть описана графом ⁴G₁, где верхний индекс означает число его вершин (см. Рис 2), а нижний - порядковый тип: