Лекция 1
1. Определение буквы, алфавита, слова, кода.
2. Определение модели. Модель- алгоритм- программа.
3. Способы представления модели алгоритмом и примеры алгоритмов описания процессов “живой природы” или явлений жизни социума.
Знак - материальный, чувственно воспринимаемый предмет (явление, действие), которое выступает как представитель другого предмета, свойства, отношения.
Значение – содержание, связываемое с тем или иным выражением (словом, предложением, знаком некоторого языка).
Буква – элементарный знак какой-либо символики, рассматриваемой вне зависимости от выражаемого им смысла.
Алфавит – конечное множество, список букв.
Слово – ряд букв некоторого алфавита.
Код – конечное или счетное множество слов в некотором алфавите.
Вообще говоря, моделирование является одним из методов познания, наряду, например, с такими как наблюдение и эксперимент. Поскольку мы ведем речь не вообще о моделировании, а о моделировании в социальных науках и, прежде всего, в социологии, то ряд методов можно продолжить, например, включив в качестве методов познания социума опросы населения и работу с документами.
Учитывая другую специфику, а именно то, что речь в нашем курсе пойдет не вообще о моделировании в социологии[1], а о специфическом виде и этапе формализации моделей - математическом моделировании, следует отметить, что выступая как метод познания, включает в себя как методику построения модели, так и методику оперирования с моделями социальных процессов и систем, в том числе и в рамках вычислительного эксперимента для получения о них нового знания.
Идея – применять математическое моделирование в целях освоения тайн живой материи – была высказана, а в биологических науках и реализована во многих удачных попытках, весьма давно. Достаточно вспомнить ряд Фибоначчи (1202), описывающий размножение кроликов, модель динамики роста популяции Т.Мальтуса (1798) или уравнение Вольтерра- Лотка (1925), описывающее динамику системы “хищник – жертва”. И это не случайно. Ибо именно на математическом языке природа, зачастую, открывает нам глубину своих тайн.
Возможно, впервые эту мысль высказал в XIX веке основатель статистической физики Виллард Гиббс на ученом заседании, на котором обсуждался вопрос о том, чему следует в учебных программах оказывать предпочтение: языкам, особенно латыни и греческому, или математике. Дискуссия длилась долго. Неожиданно обычно молчаливый В.Гиббс, попросил слова и сказал: "Математика — это тоже язык"[2].
Любой язык формируется как инструмент и продукт общения некоторой социальной общности субъектов под воздействием сложившегося их образа жизнедеятельности и ради его воспроизводства, обусловленного данным набором технологических укладов, и взаимодействующих в мировоззренческой “операционной среде”, которая имеет длительную историю своего возникновения и развития, имеющую как этнические, цивилизационные, так и религиозные, научно-культурные корни.
Если строго следовать этому тезису, то мы должны признать, что, с одной стороны, говоря о построении математической модели и вычислительном эксперименте над ней, мы, в сущности, говорим о специфической части математического языка – о языке реализации – сопровождения как самого процесса математического моделирования, так и языке сопровождения [4] вычислительного эксперимента над построенными моделями. Почему это важно, скажем несколько позже, а сейчас отметим другую сторону начатого «языкознания».
Другая сторона, заключается в том, что мы намерены, излагая этот
язык сопровождения и изложения моделирования в широком смысле, учитывать вообще закономерности, присущие языкам. Так следуя М.М.Бахтину [3], мы будем иметь в виду как изменчивую (диахронную) компоненту языковой ткани, отображенную школой Фосслера, так и сохраняющуюся (синхронную) компоненту, впервые последовательно разработанную школой Ф. Соссюра. Первая - ценна для языка творческим потенциалом, раскрытостью к творчеству новаций в языке. Вторая значима тем, что разрабатывает синтаксис и грамматику на множестве устойчивых, сложившихся языковых структур и элементов.
Рассматривая язык любой человеческой общности, например, какого-либо народа, всегда полезно – применительно к языку моделирования живых систем, социальных процессов – помнить, что в каждом языке есть множество подъязыков, ориентированных на общение внутри специфических подобщностей, например, таких больших социальных групп как молодежь или бюрократия, а равно и профессиональные подъязыки – врачей, строителей или математиков – алгебраистов, топологов и т.д.
Для нас, занимающихся моделированием социальных систем и процессов, этот подход важен потому, что, во-первых, итоговый продукт такого математического моделирования не остается достоянием только узких специалистов, а направляется в те или иные органы управления, а во-вторых, получение этого продукта – не одноактно и требует мобилизации интеллекта разных культур, что неминуемо обуславливает модельера как “полиглота” не только профессиональных подязыков.
Какими же ещё языками обязан владеть такой математик?
Прежде всего, языком предметной области, для которой строится модель. Так, если строится математическая модель этно-политического конфликта, то необходимо владеть языком этносоциологии. Но поскольку строящаяся модель, прежде чем она получит “путевку в жизнь”, будет подвергнута взыскательной критике методологов-социологов, то и этим языком модельеру надо владеть, чтобы взрастить свое детище.
Но результаты прогнозов или анализа системы предполагается вручать конкретным чиновникам–управленцам, а они, вынужденные считаться, во многом, с принципом “не навреди своему креслу”, будут брать или не брать на вооружение плоды моделирования или саму модель в зависимости от того, поверят они в ее продуктивные возможности или нет. Уже только для завоевания доверия – без чего моделирование бесплодно! - надо знать и этот язык – язык ЛПР.
Но какое это имеет отношение к математическому языку, пусть и связанному с серией языков специфических профессий, с их историей?
Грубо, эту историю языков, в том числе и математического, можно разделить на два больших периода – на до компьютерную эру и эру, когда “операционная среда” получила в качестве своего базиса инфраструктуру из средств вычислительной и сетевой техники. При этом первый период, помимо прочего, характеризуется тем, что за большим рядом формул всегда находилось хорошо обозримое множество ясных вычислительных алгоритмов, сложенных из еще более простых – таких как, например, алгебраические и тригонометрические многочлены, вполне доступные к вычислению, опираясь на ручку и листок бумаги.
Вторая половина ХХ века внесла существенные и перспективные коррективы в расширение средств математического языка, т.е. средств того, на что может опираться математик, моделирующий процессы, происходящие в социуме. Появились искусственные языки [7].
Начнем с устройства математического языка первого периода. В основе любого языка лежат слова и предложения из них. Каждое слово сложено из букв, например, слово из букв в, л, о, с. Если ограничиться этой четверкой, то это и будет алфавит для всех последующих текстов. Например, ряда слов: вол, лов, волос, соло, олово, Осло или предложений: Лов сов в Осло или соло ослов в Волосово. Очевидны ограниченные возможности отражения действительности, оставаясь в рамках такого алфавита.
Мы настолько привыкли читать и говорить словами, что почти не обращаем внимание на буквы, из которых они сложены. Однако, когда текст короткий, и написан незнакомой рукой, или к тому же он еще и поврежден, то мы начинаем вглядываться в буквы слов, начинаем различать их как знаки. Но именно со знаков и начинают строиться языки.
Каждый из нас со школы знает, что есть буквы-знаки русского языка, а есть математические знаки, например:
å -знак суммы; Ö -знакквадратного корня; > -знак “больше”;
Ú - знак “или”; ± -знаки сложения и вычитания; Ð - знак угла.
Уже на основе этого “школьного” множества знаков можно сказать, что есть знаки, выражающие некоторые вычислительные операции, например, сложения, извлечения корня или вычитания, но есть и знаки, обозначающие некоторые математические объекты, например, углы, также как и есть знаки, определяющие отношения между математическими объектами.
Наверно, не надо иметь “семи пядей во лбу”, чтобы самостоятельно высказать свое мнение по поводу такой записи из математических знаков:
ÐА > 0; ÐВ > 0; ÐА + ÐВ > ÐА Ú ÐВ
Вы, конечно, заметили, что эту запись вполне можно выразить словами: пусть угол А больше нуля и угол Б больше нуля, тогда, результат их суммирования будет больше любого из слагаемых углов. Но вы также наверняка оценили, насколько компактней и прозрачней выражена основная мысль! Вот, что значит энергетика знака – и мы к этому повороту размышлений еще вернемся в разделе, когда будем вести речь о так называемом когнитивном моделировании. А пока, чтобы тайна “когнитивных карт”, выраженных в очень древних иероглифах, вас немного заинтриговала, запишу для вас загадку – что бы это могло означать?







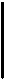








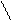


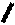











Доверьтесь своей интуиции, помните, что многие иероглифы идут от наиболее значимых в устойчивом образе жизни предметов, сходных и по назначению и конфигурации. Что-то из них- это вид сверху, а что-то и вид сбоку. А вообще-то это попытка записать строки хайку китайскими иероглифами.
Итак, математический язык! Прежде всего, он, этот язык, абстрактный в противоположность языкам этносов, где каждое слово имеет свое конкретное значение. Язык математических знаков обладает большей универсальностью, он используется во всех сферах человеческой деятельности и опирается он на ту общечеловеческую практику, современниками которой еще являются многие ваши отцы и деды, получавшие образование в большей части ХХ века.
Система математических знаков является достоянием всего человечества, она вырабатывалась на протяжении тысячелетий. Математический язык является результатом усовершенствования естественного языка по различным направлениям: 1) устранение громоздкости естественного языка; 2) устранение его двусмысленности; 3) расширение его выразительных возможностей. Он употребляется как средство выражения математической мысли.
Язык в широком смысле, если пользоваться филологической аналогией, — это словарь, грамматика, рассказы, повести, пьесы и романы, написанные на этом языке. Что же в математическом языке является аналогом слов и грамматики, а что — рассказов и повестей? Аналогом слов и грамматики является математическая операционная система ( её фрагмент приведен перед хайку), а пьес и прочего — математические модели.
При этом, если математическая операционная система первой докомпьютерной фазы имела общий и весьма доступный базис материальных инструментов коммуникации – мел и доску, карандаш и бумагу, то во второй фазе скачкообразно усложняется этот базис, но зато и расширяется множество опор, которые служат моделированию социальных процессов и систем, а значит и расширяется сам язык. Овладение математическим языком любой из названных фаз предполагает сознательное усвоение содержания математических понятий, отношений между ними (аксиом, теорем) и умение рационально и грамотно выразить математическую мысль соответствующими языковыми средствами, а также свободное оперирование всем этим в практической деятельности.
Математическая формализация - это описание какого-то фрагмента реальности с помощью математического языка[3].
Логическая формализация (до математическая или пред математическая)– описание какого-то реального явления или объекта с помощью формальной логики. Логическая формализация может быть пред математической, если проводится с целью образования базиса для математизации представлений о реальности, или до математической, если не преследует этой цели.
Формализация может различаться по степени четкости. Так, математическая наиболее четкая, пред математическая формализация менее четкая, чем математическая, и. наконец, до математическая формализации наименее четкая из всех видов.
Если предположить, что целью исследования некоторого реального объекта или явления является получение наиболее четкого знания о нем, то можно рассматривать до математическую и пред математическую формализации как этапы, предшествующие формализации математической.
«Сама возможность формализации научных представлений о любом предмете свидетельствует о достижении достаточно высокого уровня знания. Ввести какой бы то ни было формализм – значит иметь довольно четкое представление о том, что мы изучаем. Пока такой четкости нет, никакой формализм невозможен»[4].
Формализация имеет ряд неоспоримых достоинств: дает возможность четко обрисовать круг достигнутых результатов и выявить совокупность нерешенных задач[5]. Кроме того, формализация является основой для применения методологии математического моделирования, другими словами, моделирование без формализации невозможно.






