Обозначим условие предельного перехода в виде 
. Здесь под обозначением 
будем понимать x 0 или 
.
Пусть f (x) и g (x) — функции, для которых существуют пределы при 
, т. е.
, 
.
Кроме того, пусть c — постоянная величина.
Сформулируем основные теоремы о пределах функций.
1. Постоянный множитель можно выносить за знак предела
.
2. Предел алгебраической суммы функций равен алгебраической сумме пределов этих функций
.
3. Предел произведения функций равен произведению пределов этих функций
.
Теоремы по п.п. 2-3 можно распространить на любое конечное число функций.
4. Предел частного двух функций равен частному пределов этих функций при условии, что предел делителя не равен нулю
, где 
.
5. Если 
, 
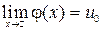, то предел сложной функции равен
.
6. Если в некоторой окрестности точки x 0 или при достаточно больших x выполняется условие 
, то
.
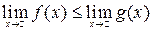Замечательные пределы. Два часто используемых при решении задач предела называют замечательными пределами:
1. 
. Если аргумент x является функцией f (x), то 
.
2. 
. Аналогично 
.
В первом замечательном пределе, как и везде в курсе высшей математики, аргумент синуса берется в радианах. Второй замечательный предел равен иррациональному числу е, являющемуся основанием натуральных логарифмов и приближенно равному 2,72.
Второй замечательный предел иногда записывают в следующей форме:
или 
.
Асимптоты графика функции
Асимптотой графика функции y = f (x) называется прямая, расстояние до которой от точки графика стремится к нулю при неограниченном удалении точки графика от начала координат.
Различают 3 вида асимптот:
а) вертикальная асимптота. Ее уравнение x = a. График функции y = f (x), имеющий вертикальную асимптоту, может иметь вид, показанный на рис. 5.5.
Для нахождения вертикальной асимптоты графика функции y = f (x) достаточно найти точку a такую, что в этой точке хотя бы один односторонний предел бесконечен, т. е.
или/и 
.
Тогда прямая x = a является вертикальной асимптотой графика функции y = f (x).
б) горизонтальная асимптота. Ее уравнение y = b. График функции y = f (x)изображен на рис. 5.6.
 |
Рис. 5.6. Горизонтальная асимптота
Если
или/и 
,
то прямая y = b является горизонтальной асимптотой (справа на 
; слева на 
) графика функции y = f (x). Если оба эти предела бесконечны или не существуют, то график функции y = f (x) горизонтальных асимптот не имеет. Если горизонтальных асимптот нет, то отыскивают наклонную асимптоту.
в) наклонная асимптота. Ее уравнение y = kx + b. График функции, имеющий наклонную асимптоту, изображен на рис. 5.7.
 |
Рис. 5.7.Наклонная асимптота
Если существуют конечные пределы
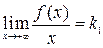и 
,
то прямая y = k 1 x + b 1 является наклонной асимптотой справа графика функции y = f (x).
Если существуют и конечные пределы
, 
,
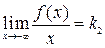то прямая y = k 2 x + b 2 является наклонной асимптотой слева.
Если хотя бы один из пределов при 
и при 
бесконечен или не существует, то график функции y = f (x) наклонных асимптот не имеет.
Заметим, что на рис. 3.7 прямая y = kx + b является одновременно наклонной асимптотой слева и справа (т. к. k = k 1 = k 2; b = b 1 = b 2).
Нетрудно видеть, что если k = 0, то наклонная асимптота превращается в горизонтальную, т. е. горизонтальная асимптота представляет собой частный случай наклонной асимптоты при k = 0.
3.8. Непрерывность функции в точке и на отрезке
Функция y = f (x) называется непрерывной в точке x 0, если выполняются три условия:
1. Существует f (x 0), т. е. значение функции в точке x 0.
2. Существует конечный предел 
.
3. 
.
Очевидно, что если функция y = f (x) непрерывна в точке x 0, то ее график можно провести через эту точку, не отрывая карандаша от бумаги (отсюда и название).
Если в точке x 0 не выполняется хотя бы одно из трех указанных выше условий, то функция y = f (x) не является непрерывной (терпит разрыв) в точке x 0.
Невыполнение каждого из условий можно проиллюстрировать рис. 5.8.
Не выполняется:
 |
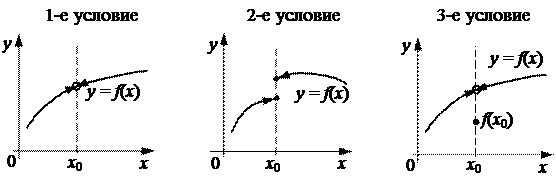Рис. 5.8. Невыполнение условий непрерывности функции
Можно доказать следующие свойства функций непрерывных в точке:
1. Если функции f (x) и g (x) непрерывны в точке x 0, а с — постоянная величина, то функции
c f (x); 
; 
; 
, где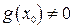 
также непрерывны в точке x 0 .
2. Если функция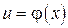 
непрерывна в точке x 0 , а функция f (u) непрерывна в точке u 0 , то сложная функция
непрерывна в точке x 0 .
Таким образом, знак предела можно вносить под знак непрерывной функции, т. е.
.
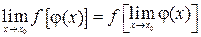3. Все элементарные функции непрерывны во всех точках, принадлежащих области их определения.
Функция y = f (x) называется непрерывной на отрезке [ a, b ] (интервале (a, b)), если она непрерывна в каждой точке этого отрезка (интервала).
Если функция y = f (x) в точке x 0 не является непрерывной, то точка x 0 называется точкой разрыва функции y = f (x).
Принята следующая классификация точек разрыва:
1. Если в точке разрыва x 0 функции y = f (x) существует конечный предел , то x 0 называется точкой устранимого разрыва функции y = f (x) (рис. 3.8, условие 1 и условие 3).
2. Если в точке разрыва x 0 функции y = f (x) существуют конечные односторонние пределы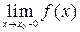 
и 
, то x 0 называется точкой разрыва первого рода (рис. 3.8, условие 2).
Точки устранимого разрыва также можно отнести к точкам разрыва 1-го рода, т. к. в этих точках существуют конечные односторонние пределы функции y = f (x).
3. Если в точке разрыва x 0 функции y = f (x) хотя бы один из односторонних пределов не существует или бесконечен, то x 0 называется точкой разрыва второго рода функции y = f (x).
Возвращаясь к вопросу нахождения вертикальных асимптот, можно сформулировать следующий признак существования вертикальной асимптоты:
если x 0 – точка разрыва 2-го рода функции y = f (x) и хотя бы один из односторонних пределов функции в этой точке бесконечен, то прямая x = x 0 является вертикальной асимптотой графика функции y = f (x).
