Предел функции в точке и в бесконечности

Рассмотрим сначала понятие предела функции в точке. Пусть функция y = f (x) определена в некоторой окрестности точки x ₀ кроме, может быть, самой точки x ₀. Будем рассматривать поведение f (x) при приближении независимой переменной x к точке x ₀.

Графически понятие предела можно ввести следующим образом. Говорят, что функция y = f (x) имеет пределом число а в точке x ₀ , если при движении по графику функции так, что абсцисса точки графика приближается к x ₀ слева или справа, ордината этой точки приближается к значению a (рис. 3.2). При этом по графику приближаемся к точке А.

Обозначают этот факт так

.

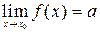Запись под обозначением «lim» называется условием предельного перехода. Здесь это условие .

 

Существует несколько математических определений предела функции в точке. Наиболее употребительным из них является определение по Коши, также называемое определением на языке .

 

Число a называется пределом функции y = f (x) в точке x ₀ тогда и только тогда, когда для любого числа > 0 найдется такое число > 0, зависящее от , что для любого x,не равного x ₀ и удовлетворяющего неравенству 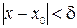, следует .

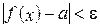Используя математические символы, это определение можно записать следующим образом:

.

 

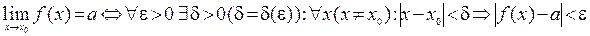Пусть задано некоторое число > 0. Из определения предела следует, что если число a является пределом функции y = f (x) в точке x ₀ , то при этом должно существовать число такое, что как только независимая переменная x попадает в вертикальную полосу от до 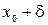, то значение функции f (x) попадает в горизонтальную полосу от до (см. рис. 5.2).

 

 

 

Рис. 5.2. Предел функции в точке

 

 

Как видно из рис. 5.2, также существует число для . Таким образом, если для каждого малого положительного числа найдется такое число , то тогда число a является пределом функции y = f (x) в точке x ₀.

 

Можно говорить об односторонних пределах функции f (x) в точке x ₀ слева или справа. При определении таких пределов рассматриваются значения x, которые соответственно меньше или больше, чем x ₀ .

Такие пределы обозначаются: слева и справа 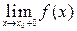. На рис. 5.3 графически показан случай, когда существуют односторонние пределы функции y = f (x) слева и справа, но предел функции в точке x ₀ не существует.

Из рис. 3.3 видно, что для функции y = f (x), представленной на графике,

; .

Для существования предела функции в точке x ₀ необходимо и достаточно, чтобы выполнялось условие

.

 

Аналогично можно ввести определение предела функции и при стремлении независимой переменной x к бесконечности. Пусть функция y = f (x) определена при достаточно больших по абсолютной величине значениях независимой переменной x.

Тогда число a называется пределом функции y = f (x) в бесконечности тогда и только тогда, когда для любого числа > 0 найдется такое число S > 0, зависящее от , что для любого x, удовлетворяющего неравенству | x | > S, следует | f (x) – a | < .

Используя математические символы, это определение можно записать следующим образом:

.

 

Аналогично односторонним пределам в точке можно ввести односторонний предел функции в бесконечности при и при .

При рассматривают только такие значения x, которые больше S, а при — те, которые меньше – S.

Пределы 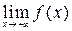и могут быть разными (рис. 5.4).

 

 

 

 

 

Рис. 5.4. Пределы функции на бесконечностях разных знаков

 

 

Из рис. 3.4 видно, что .