Рассмотрим сначала понятие переменной величины, или просто переменной.
Переменная величина х определяется множеством тех значений, которые она может принять в рассматриваемом случае. Это множество X назовем областью изменения значений переменной x.
Главным предметом изучения в математике является, однако, не изменение одной переменной самой по себе, а зависимость между двумя или несколькими переменными при их совместном изменении. Во многих случаях переменные не могут принимать любую пару значений из своих областей изменения; если одной из них придано конкретное значение, то этим уже определяется и значение другой. Тогда первая из них называется независимой, а вторая – зависимой переменной.
Пусть даны две переменные x и y с областями изменения X и Y. Если при этом каждому элементу x 
X по определенному правилу f поставлен в соответствие единственный элемент y 
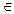Y, то говорят, что на множестве X задана функция y = f (x).
Ясно, что при этом переменная x является независимой переменной. Ее часто называют аргументом функции.
Переменная y является зависимой переменной и называется значением функции, или просто функцией.
Множество X называется областью определения функции, а множество Y — областью ее значений.
Существует ряд способов задания функции:
а) наиболее простой — аналитический способ, т. е. задание функции в виде формулы. Если область определения функции X при этом не указана, то под X подразумевается множество значений x, при которых формула имеет смысл;
б) графический способ. Этот способ особенно нагляден. Для функции одной переменной y = f (x) используется координатная плоскость (xy).
Совокупность точек y, соответствующих заданным значениям x, определяет график функции на плоскости (xy);
в) табличный способ. Он часто используется, когда независимая переменная x принимает лишь конечное число значений.
5.2. Основные свойства функций
Рассмотрим основные свойства функций, которые упрощают проведение их исследования:
Четность. Функция y = f (x) называется четной, если для любого значения x, принадлежащего области определения функции X, значение (– x) тоже принадлежит X и при этом выполняется
f (–x) = f (x).
График четной функции симметричен относительно оси ординат.
Функция y = f (x) называется нечетной, если для любого x 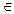X следует (– x) 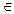X и при этом
f (–x) = – f (x).
График нечетной функции симметричен относительно начала координат.
Если функция y = f (x) не является ни четной, ни нечетной, то ее часто называют функцией общего вида.
Монотонность. Функция y = f (x) называется возрастающей на некотором интервале (a, b), если для любых x 1, x 2 (a, b), таких,
что x 1 < x 2, следует, что f (x 1) < f (x 2), и убывающей, если f (x 1) > f (x 2).
Возрастающую и убывающую на интервале (a,b) функции называют монотонными на этом интервале, а сам интервал (a,b) — интервалом монотонности этих функций.
В некоторых учебниках такие функции называют строго монотонными, а монотонными называют неубывающую и невозрастающую на рассматриваемом интервале функции (вместо строгих неравенств для функций пишутся нестрогие).
Ограниченность. Функция y = f (x) называется ограниченной на интервале (a, b), если существует такое число С > 0, что для любого x 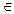(a, b) следует |f (x) | < C, и неограниченной в противном случае, т. е. если для любого числа C > 0 существует такой x 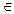(a, b), что |f (x) | > C. На рис. 5.1 показан график функции, ограниченной на интервале (a, b).
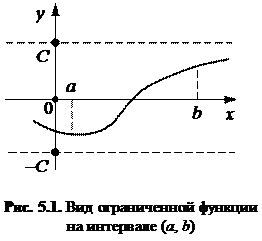
Аналогичное определение ограниченности можно дать для любого вида промежутка.
Периодичность. Функция y = f (x) называется периодической, если существует такое число t, что для любого x X выполняется
f (x + t) = f (x).
Наименьшее из таких чисел t называется периодом функции и обозначается Т.
Характерным признаком периодичности функций является наличие в их составе тригонометрических функций.
5.3. Элементарные функции и их графики
К элементарным функциям относятся:
а) простейшие элементарные функции
1. Константа y = c, где с — постоянное для данной функции действительное число, одно и то же для всех значений x.
 |
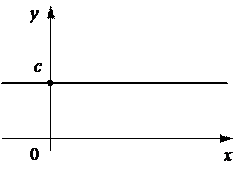2. Степенная функция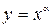 
, где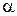 
— любое постоянное действительное число, кроме нуля. Вид графиков функций при некоторых целых положительных (
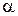= n), целых отрицательных ( 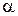= – n) и дробных ( 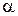= 1/ n) значениях представлен ниже.
 | |||
|
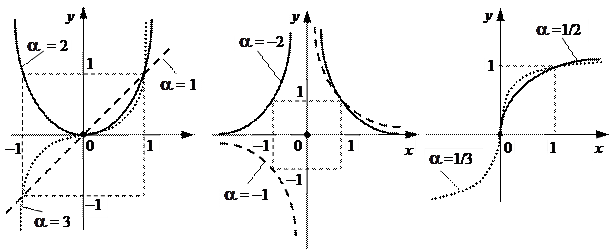3. Показательная функция y = ax (a > 0; a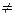 
1).
 |
4. Логарифмическая функция y = log a x (a > 0; a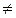 
1).
 |
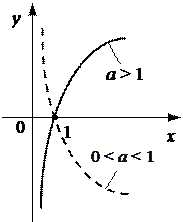5. Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x.
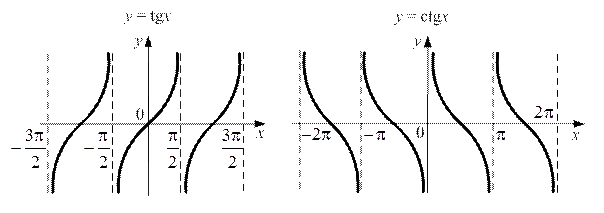
6. Обратные тригонометрические функции.
y = arcsin x y = arccos x
 |  | ||
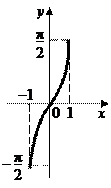y = arctg x y = arcctg x
 |
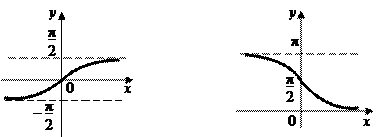б) сложные функции
Кроме перечисленных простейших элементарных функций аргумента x к элементарным функциям также относятся функции, аргументами которых являются тоже элементарные функции, а также функции, полученные путем выполнения конечного числа арифметических действий над элементарными функциями. Например, функция
тоже является элементарной функцией.
Функции, аргументами которых являются не независимые переменные, а другие функции, называются сложными функциями или суперпозициями функций. Пусть даны две функции: y = sin x и z = log2 y. Тогда сложная функция (суперпозиция функций) может иметь вид
z = log2 (sin x).
Также можно ввести понятие обратной функции. Пусть y = f (x) задана в области определения X, а Y — множество ее значений. Выберем какое-нибудь значение y = y 0 и по нему найдем x 0 так, чтобы y 0 было равно f (x 0).Подобных значений x 0 может оказаться и несколько.
Таким образом, каждому значению y из Y ставится в соответствие одно или несколько значений x. Если такое значение x только одно, то в области Y может быть определена функция x = g (y), которая называется обратной для функции y = f (x).
Найдем, например, обратную функцию для показательной функции y = ax. Из определения логарифма следует, что если задано значение y, то значение x, удовлетворяющее условию y = ax, находится по формуле x = log a y. То есть каждому y из Y можно поставить в соответствие одно определенное значение x = log a y.
Следовательно, функция x = log a y является обратной для функции y = ax на множествах X и Y. Так как принято у любой функции независимую переменную обозначать x, то в этом случае говорят, что y = f (x) и y = g (x) — обратные функции.
Графики функции y = f (x) и обратной ей функции y = g (x) симметричны относительно биссектрисы 1-го и 3-го координатных углов.
