Должны содержать заключение о значимости коэффициентов регрессии, уравнение регрессии и заключение о его адекватности поверхности отклика исследуемого объекта.
Оформить результаты работы в виде отчета по лабораторной работе в соответствии с требованиями (см. стр. 5).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие задачи решает теория планирования эксперимента? Какие требования предъявляются к объектам, факторам и параметрам оптимизации в планировании эксперимента?
2. В чем сущность планирования эксперимента? Дайте определение факторному пространству. Поясните разницу между активным и пассивным экспериментом.
3. Что дает полный факторный эксперимент, и с какой целью вводят новые переменные? В чем сущность и цели стандартизации масштаба факторов?
4. Как выбрать уровни варьирования факторов?
5. В чем сущность рандомизации?
6. Что собой представляет математическое и геометрическое описание объекта в трехфакторном эксперименте?
7. Как составляется и какими свойствами обладает матрица планирования ПФЭ?
8. Что такое взаимодействие факторов, что они дают и сколько их в ПФЭ?
9. Каков порядок постановки опытов при ПФЭ?
10. Как проверить воспроизводимость опытов?
11. Как рассчитать оценки коэффициентов регрессионного уравнения?
12. Как проверить статистическую значимость оценок коэффициентов регрессии?
13. Как проверить адекватность полученной математической модели?
14. Какими правилами руководствуются, проводя анализ уравнения регрессии и исследуемых параметров оптимизации?
Лабораторная работа №5
ПОСТРОЕНИЕ И АНАЛИЗ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ МЕТОДОМ ДРОБНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА
Цель работы: изучение основ теории планирования эксперимента, приобретение навыков построения матрицы планирования и математической модели исследуемых объектов с помощью дробного факторного эксперимента.
Задание: 1. Изучить особенности планирования эксперимента методом дробных реплик;
2. Получить адекватное уравнение регрессии, с помощью дробного факторного эксперимента, описывающее влияние факторов на качество конкретной продукции в соответствии с заданием.
Основные сведения
Количество опытов в ПФЭ быстро растет с увеличением числа факторов и значительно превосходит число определяемых коэффициентов линейной модели, что свидетельствует о большой избыточности опытов ПФЭ. Для уменьшения числа опытов из множества точек факторного пространства может быть отобрана их некоторая часть, содержащая подходящее число опытов и представляющая собой план дробного факторного эксперимента (ДФЭ). Геометрическое изображение трансфор-мации плана ПФЭ типа 23 в план ДФЭ типа 23-1 представлено на рис. 5.1.

Рис. 5.1. Графическое изображение планов ПФЭ и ДФЭ в факторном пространстве: а – методом проекции на три плоскости; б – по четырем точкам, не лежащим в одной плоскости
План ПФЭ 23 имеет вид куба с восьмью вершинами (точками плана), а возможные планы ДФЭ типа 23-1 имеют вид проекций этого куба на плоскости, то есть из восьми точек куба выбираются четыре (рис. 5.1 а). Из куба можно также выбрать четыре точки из восьми, не лежащие в одной плоскости, и построить план ДФЭ типа 23-1 (рис. 5.1 б).
Дробным факторным экспериментом называется система опытов, представляющая собой часть ПФЭ, позволяющая рассчитать коэффициенты уравнения регрессии и сократить объем экспериментальных данных.
Дробный факторный эксперимент, как и ПФЭ, позволяет исследовать полиномиальные математические модели (ММ) вида:
y = b0 + b 1 x 1 + b2 x 2 +…+b пxп + b12 x 1 x 2 + b13 x 1 x 3+… + b п –1, п xп –1 xп
Число оцениваемых коэффициентов ММ и число проводимых в эксперименте опытов связано с понятием насыщенности эксперимента. Если число проводимых опытов превышает число оцениваемых коэффициентов, то эксперимент называется ненасыщенным, если равно – насыщенным.
Для нахождения математического описания процесса используются определённые части ПФЭ: ½; ¼; 1/8; 1/16 и т.д. Эти системы опытов называются дробными репликами, а сам метод ДФЭ – методом дробных реплик. Возможные дробные реплики от ПФЭ типа 24 представлены в таблице 5.1.
Таблица 5.1. Возможные дробные реплики от ПФЭ типа 24
| № | Факторы | Yj | Дробные реплики | ||||||
| Х0 | Х1 | Х2 | Х3 | Х4 | |||||
| + | - | - | - | - | у1 | 1/8 | 1/4 | 1/2 | |
| + | + | - | - | - | у2 | ||||
| + | - | + | - | - | у3 | 1/8 | |||
| + | + | + | - | - | у4 | ||||
| + | - | - | + | - | у5 | 1/8 | 1/4 | ||
| + | + | - | + | - | у6 | ||||
| + | - | + | + | - | у7 | 1/8 | |||
| + | + | + | + | - | у8 | ||||
| + | - | - | - | + | у9 | 1/8 | 1/4 | 1/2 | |
| + | + | - | - | + | у10 | ||||
| + | - | + | - | + | у11 | 1/8 | |||
| + | + | + | - | + | у12 | ||||
| + | - | - | + | + | у13 | 1/8 | 1/4 | ||
| + | + | - | + | + | у14 | ||||
| + | - | + | + | + | у15 | 1/8 | |||
| + | + | + | + | + | у16 |
Матрица ДФЭ типа 24-1 из восьми опытов для четырех факторного планирования будет полурепликой от ПФЭ типа 24, а для пятифакторного планирования – четверть репликой от 25. В последнем случае два линейных эффекта приравниваются к эффектам взаимодействия. Для обозначения дробных реплик, в которых p линейных эффектов приравнены к эффектам взаимодействия, вводится обозначение 2 k-p, где р –число линейных эффектов, приравненных к эффектам взаимодействия, k-p является показателем дробности плана ПФЭ.
Так, при р =1 число опытов в плане ДФЭ в два раза меньше, чем в плане ПФЭ, и поэтому такие планы называются полуреплика плана ПФЭ 23. Они записываются в виде 23-1. При р =2 число опытов сокращается в четыре раза и такие планы называются четверть-реплика. Например, плана ПФЭ 25 имеет 32 опыта, а в плане ДФЭ в виде четверть-реплики, число опытов сокращается до восьми и она записывается как 25-2. При р =3 для ДФЭ 26-3, число опытов сокращается с 64 до 8. Условные обозначения дробных реплик и количество опытов представлены в таблице 5.2.
Таблица 5.2 Условные обозначения дробных реплик и количество опытов
| Число факторов | Дробная реплика | Условное обозначение | Число опытов | |
| для дробных реплик | для полного факторного эксперимента | |||
| 1/2 – реплика от 23 | 23–1 | |||
| 1/2 – реплика от 24 | 24–1 | |||
| 1/4 – реплика от 25 | 25–2 | |||
| 1/8 – реплика от 26 | 26–3 | |||
| 1/16 – реплика от 27 | 27–4 | |||
| 1/2 – реплика от 25 | 25–1 | |||
| 1/4 – реплика от 26 | 26–2 | |||
| 1/8 – реплика от 27 | 27–3 | |||
| 1/16– реплика от 28 | 28–4 | |||
| 1/32-реплика от 29 | 29–5 | |||
| 1/64-реплика от 210 | 210–6 | |||
| 1/128-реплика от 211 | 211–7 | |||
| 1/256-реплика от 212 | 212–8 | |||
| 1/512-реплика от 213 | 213–9 | |||
| 1/1024-реплика от 214 | 214–10 | |||
| 1/2048-реплика от 215 | 215–11 |
При выборе дробности р необходимо учитывать, что число опытов (2 k-p)должно быть больше числа членов уравнения (k+1), т.е. должно соблюдаться условие:
k+1 ≤ 2 k-p (5.1)
Способ сокращения числа экспериментов можно сформулировать в виде общего правила. Чтобы сократить число опытов, нужно дополнительно вводимый в эксперимент фактор варьировать как вектор–столбец матрицы, соответствующий взаимодействию, которым можно пренебречь. Тогда изменение уровней нового фактора определится знаками этого вектор–столбца.
Выбранное для дополнительного фактора взаимодействие (произведение) называется генерирующее соотношение или генератором плана. ДФЭ типа 2 k-p будет иметь р генераторов.
Рассмотрим правила построения плана ДФЭ полуреплики типа 23-1 от ПФЭ 23, где k =3 (число факторов), р =1 (число линейных эффектов, приравненных к эффектам взаимодействия), N=4 (число опытов). План ДФЭ полуреплики типа 23-1 имеет вид (табл. 5.3).
| Таблица 5.3. План ДФЭ типа 23-1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Первые два фактора x 1 и x 2 варьируем, как и в ПФЭ типа 22, а для третьего фактора выбираем генерирующее соотношение в виде x 3 = x 1 x 2
Для полинома:
y = b 0 + b 1x1 + b 2x2 + b 3x3 + b 12x1x2 + b 13x1x3+ b 23x2x3+ b 123 x1x2 x3
количество столбцов плана составляет восемь.План является ортогональным, но в нем оказались четыре пары одинаковых столбцов: 1 и 8; 2 и 7; 3 и 6; 4 и 5. Поэтому можно определить не восемь, а только четыре коэффициента, отражающие совместное влияние двух одинаковых столбцов:
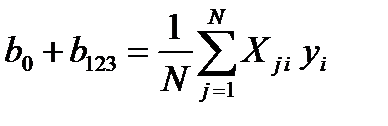 (5.2)
(5.2)
Суммарные значения коэффициентов b1 + b23, b2 + b13, b3 + b12 определяются аналогично. Это следствие попытки определить полное количество коэффициентов (8) по недостающему числу опытов (4). Однако если заранее известно, что некоторые из членов уравнения равны нулю или пренебрежительно малы или имеется априори информация о величинах некоторых коэффициентов, то они могут быть вычленены, т.е. исключены.
Так, если b 123 =0, то
 (5.3)
(5.3)
Если можно допустить, что коэффициенты из их смешанной оценки сопоставимы, то для рассматриваемого плана
 (5.4)
(5.4)
Достоинством планов ДФЭ является то, что если построенный на его основе полином не удовлетворяет требованиям по точности, то план ДФЭ легко достраивается до плана ПФЭ, без потери информации о прежних опытах, с формированием более точного уравнения регрессии.
При построении полуреплик ДФЭ типа 23-1 существует всего две возможности: приравнять х3 к (+ x 1 x 2)или к (– x 1 x 2). Поэтому можно построить только две полуреплики 23-1 (табл. 5.4).
Таблица 5.4. Две полуреплики ДФП 23-1 от ПФЭ 22
| № опыта | x 1 | x 2 | x 3 | x 1 x 2 x 3 |
| + | + | + | + | |
| – | – | + | + | |
| + | – | – | + | |
| – | + | – | + |
| № опыта | x 1 | x 2 | x 3 | x 1 x 2 x 3 |
| + | + | – | – | |
| – | – | – | – | |
| + | – | + | – | |
| – | + | + | – |
или
Для произведения трех столбцов первой матрицы выполняется соотношение: +1= x 1 x 2 x 3, а для второй матрицы: -1= x 1 x 2 x 3.
Символическое обозначение произведения столбцов, равного (+1) или (–1), называется определяющим контрастом.
Контраст помогает определять смешанные эффекты. Для того, чтобы определить, какие эффекты смешаны в анализируемом эффекте, нужно помножить обе части определяющего контраста на столбец, соответствующий данному эффекту.
Так, если +1= x 1 x 2 x 3, то для x 1 имеем x 1= x 12 x 2 x 3= x 2 x 3, так как всегда x 12 = 1. Для x 2 находим x 2= x 1 x 22 x 3= x 1 x 3, для x 3 находим x 3= x 1 x 2 x 32= x 1 x 2.
Это значит, что коэффициенты линейного уравнения будут оценками
b1=β1 + β 23, b2= β 2 + β 13, b3= β 3 + β 12.
Соотношение, показывающее, с каким из эффектов смешан данный эффект, называется генерирующим соотношением.
Полуреплики, в которых основные эффекты смешаны с двухфакторными взаимодействиями, носят название планов с разрешающей способностью III (по наибольшему числу факторов в определяющем контрасте). Такие планы принято обозначать:  .
.
В зависимости от числа факторов, входящих в контраст, говорят о разрешающей способности ДФЭ. Так если для ДФЭ типа 24-1 в качестве генератора плана выбрано x 4= x 1 x 2 x 3 (контраст соответственно 1= x 1 x 2 x 3 x 4), то говорят, что у такого эксперимента разрешающая способность равна 4; если генератор x 4= x 1 x 2 и контраст 1 = x 1 x 2 x 4, то разрешающая способность равна 3.
Генератор плана с наибольшей разрешающей способностью называют главным и ему отдают предпочтение.
Если вводится не один, а несколько дополнительных факторов, то мы получаем несколько генераторов плана (для каждого дополнительного фактора свой). В этом случае для определения смешанности оценок коэффициентов используют обобщающий контраст, который состоит из отдельных контрастов, а также их произведений во всевозможных сочетаниях.
При построении полуреплики 24-1 возможны восемь решений для x 4:
1. x 4= x 1 x 2, 2. x 4= - x 1 x 2, 3. x 4= x 2 x 3, 4. x 4= - x 2 x 3,
5. x 4= x 1 x 3, 6. x 4= - x 1 x 3, 7. x 4= x 1 x 2 x 3, 8. x 4= - x 1 x 2 x 3.
Разрешающая способность этих полуреплик различна. Так, реплики 1–6 имеют по три фактора в определяющем контрасте, а 7–8 по четыре. Реплики 7 и 8 имеют максимальную разрешающую способность и называются главными.
Разрешающая способность задается системой смешивания данной реплики. Она будет максимальной, если линейные эффекты смешаны с эффектами взаимодействия наибольшего возможного порядка.
При отсутствии априорной информации об эффектах взаимодействия экспериментатор стремится выбрать реплику с наибольшей разрешающей способностью, так как тройные взаимодействия обычно менее важны, чем парные. Если существует информация об эффектах взаимодействия, то она должна использоваться при выборе реплики.
Реплики, в которых нет ни одного главного эффекта, смешанного с другим главным эффектом или парным взаимодействием, а все парные взаимодействия смешаны друг с другом, носят название планов с разрешающей способностью IV (по наибольшему числу факторов в определяющем контрасте). Они имеют обозначение  . Такие полуреплики называют главными полурепликами, так как они обладают наибольшей разрешающей способностью.
. Такие полуреплики называют главными полурепликами, так как они обладают наибольшей разрешающей способностью.
Допустим, что мы полуреплику 24-1 задали генерирующим соотношением x 4= x 1 x 2 x 3. Определяющим контрастом полуреплики является соотношение: 1= x 1 x 2 x 3 x 4.
Тогда совместные оценки коэффициентов уравнения регрессии будут определяться следующим образом:
x 0 = x 1 x 2 x 3 x 4 b0= β 0 + β 1234
x 1 = x 2 x 3 x 4 b1= β 1 + β 234
x 2 = x 1 x 3 x 4 b2= β 2 + β 134
x 3 = x 1 x 2 x 4 b3= β 3 + β 124
x 4 = x 1 x 2 x 3 b4= β 4 + β 123
x 1 x 2 = x 3 x 4 b12= β 12 + β 34
x 1 x 3 = x 2 x 4 b13= β 13 + β 24
x 1 x 4 = x 3 x 2 b14= β 14 + β 32
В практических задачах тройные и более высокого порядка взаимодействия значительно чаще, чем двойные - равны нулю, и ими обычно можно пренебречь. В этом случае раздельными оценками будут b1,b2, b3, b4, так как тройными взаимодействиями β 234, β 134, β 124, β 123 вследствие их незначительности можно пренебречь.
Тогда уравнение регрессии будет иметь вид:
y = b0 + b 1x1 + b2x2 + b3x3 + b4x4 + b12x1x2+ b13x1x3+ b14 x1 x4,
и число степеней свободы равно нулю, так как число коэффициентов регрессии равно число опытов в эксперименте.
При выборе полуреплики 25-1 в распоряжении экспериментатора имеется множество вариантов:
1. х 5 можно приравнять к одному из шести парных взаимодействий. В этом случае получим полуреплику с разрешающей способностью III. Очевидно, это будет не лучший выбор полуреплики;
2. х 5 можно приравнять к одному из четырех тройных взаимодействий. Тогда получим план с разрешающей способностью IV, и все линейные эффекты будут смешаны с тройными взаимодействиями;
3. полуреплика может быть задана генерирующими соотношениями x 5 = x 1 x 2 x 3 x 4 или x 5 =- x 1 x 2 x 3 x 4.
Определяющими контрастами в этом случае будут +1= x 1 x 2 x 3 x 4 x 5 и -1= x 1 x 2 x 3 x 4 x 5. Такие реплики носят название планов с разрешающей способностью V и обозначаются  .
.
Полурепликами 26-1 редко пользуются на практике. Ведь полуреплика 26-1 требует 32 опыта, а для экспериментатора выгодны планы 26-2 или 26-3 требующие соответственно 16 и 8 опытов. Поэтому с ростом числа факторов возрастает дробность применяемых реплик.
Заметим, что при построении главных полуреплик в определяющий контраст надо включать наибольшее число факторов.
При оценивании параметров функции отклика используются также и реплики более высокой дробности. Система смешения линейных эффектов и эффектов взаимодействий между собой получается более сложной, чем при применении полуреплик. Для нахождения системы смешивания строятся обобщенные определяющие контрасты: для этого исходные контрасты перемножаются сначала попарно, получаются контрасты первого уровня. Затем контрасты первого уровня снова перемножаются попарно, получаются контрасты второго уровня и так до тех пор, пока не будет исчерпана возможность перемножения контрастов.
Обобщающий определяющий контраст составляется путем перечисления выражений для всех сформированных контрастов.
Рассмотрим пример построения 1/4-реплики 25-2. При исследовании влияния пяти факторов можно поставить не 32 опыта, а только 8, т. е. воспользоваться репликой 25-2. Здесь возможны двенадцать решений, если х 4 приравнять парному взаимодействию, а х 5 – тройному.
x 4= x 1 x 2= x 1 x 3= x 1 x 4= x 1 x 5= x 2 x 3= x 2 x 4= x 2 x 5= x 3 x 4= x 3 x 5= x 4 x 5;
x 5= x 1 x 2 x 3= x 2 x 3 x 4= x 3 x 4 x 5= x 1 x 3 x 4= x 1 x 4 x 5= x 1 x 3 x 5= x 2 x 4 x 5 и т.п.
Допустим, выбран вариант генерирующих соотношений x 4= x 1 x 3 и x 5= x 1 x 2 x 3. Тогда определяющими контрастами являются 1= x 1 x 3 x 4 и 1= x 1 x 2 x 3 x 5.
Если перемножить эти определяющие контрасты, то получится третье соотношение, задающее элементы столбца 1= x 2 x 4 x 5.
Чтобы полностью охарактеризовать разрешающую способность реплики, необходимо записать обобщающий определяющий контраст:
1= x 1 x 3 x 4= x 1 x 2 x 3 x 5= x 2 x 4 x 5
Система смешивания оценок определяется умножением обобщающего определяющего контраста последовательно на х 1, х 2, х 3, х 4, х 5, х 1 х 2, х 1 х 5.
x 1 = x 3 x 4= x 2 x 3 x 5= x 1 x 2 x 4 x 5 b1= β 1 + β 34 + β 235 + β 1245
x 2 = x 1 x 2 x 3 x 4= x 1 x 3 x 5= x 4 x 5 b2= β 2 + β 1234 + β 135 + β 45
x 3 = x 1 x 4= x 1 x 2 x 5= x 2 x 3 x 4 x 5 b3= β 3 + β 14 + β 125 + β 2345
x 4 = x 1 x 3= x 1 x 2 x 3 x 4 x 5= x 2 x 5 b4= β 4 + β 13 + β 12345 + β 25
x 5 = x 1 x 3 x 4 x 5= x 1 x 2 x 3= x 2 x 4 b5= β 5 + β 1345 + β 123 + β 24
x 1 x 2 = x 2 x 3 x 4= x 3 x 5= x 1 x 4 x 5 b12= β 12 + β 234 + β 35 + β 145
x 1 x 5= x 3 x 4 x 5= x 2 x 3= x 1 x 2 x 4 b15= β 15 + β 345 + β 23 + β 124
Получается довольно сложная система смешивания линейных эффектов с эффектами взаимодействия первого, второго, третьего и четвертого порядков. Если, например, коэффициенты:
b12 = β 12 + β 234 + β 35 + β 145 и b15= β 15 + β 345 + β 23 + β 124,
отличаются от нуля, то возникают сомнения, можно ли пренебрегать другими парными взаимодействиями, с которыми смешаны линейные эффекты. Тогда следует поставить вторую серию опытов, выбрав нужным образом другую 1/4-реплику.
При этом можно воспользоваться методом «перевала». Смысл этого метода заключается в том, что вторая четверть-реплика получается из первой путем изменения всех знаков матрицы на обратные.
Тогда в обобщающем определяющем контрасте тройные произведения имеют знак, противоположный их знаку в первой четверть-реплике. Тройные произведения определяют парные взаимодействия в совместных оценках для линейных эффектов. Усредняя результаты обеих четверть-реплик, можно получить линейные эффекты, не смешанные с парными взаимодействиями.
Реплики большой дробности. При выборе 1/8-реплики 26-3 можно воспользоваться вектор-столбцами трех взаимодействий, например, таких:
1. x 4 = x 1 x 2, x 5 = x 1 x 3, x 6 = x 2 x 3;
2. x 4 = x 1 x 3, x 5 = x 2 x 3, x 6 = x 1 x 2 x 3;
3. x 4 = x 1 x 2, x 5 = x 2 x 3, x 6 = x 1 x 2 x 3;
4. x 4 = x 1 x 2, x 5 = x 1 x 3, x 6 = x 1 x 2 x 3;
Для каждого из этих решений можно сделать шесть перестановок. Итого получается 24 возможности выбора 1/8-реплики. Это при условии, что мы всюду выбираем положительные генерирующие соотношения.
Из четырех приведенных выше решений наименее удачно первое, поскольку все линейные эффекты смешиваются с парными взаимодействиями. Если априори известно, что из всех взаимодействий наиболее существенно х 1 х 2, то нужно выбрать второе решение, если х 1 х 3 – третье, а если х 2 х 3 – четвертое.
Допустим, мы избрали четвертое решение, предполагая, что из факторов х 4, х 5, х 6 наиболее существенным является х 4. Приравняем х 4тройному взаимодействию и запишем генерирующие соотношения:
x 4 = x 1 x 2 x 3, x 5 = x 1 x 2, x 6 = x 1 x 3.
имеем следующие определяющие контрасты:
1= x 1 x 2 x 3 x 4, 1= x 1 x 2 x 5, 1= x 1 x 3 x 6.
Если попарно перемножить эти определяющие контрасты (помним, что x i2 =1), то получим: 1= x 3 x 4 x 5, 1= x 2 x 4 x 6, 1= x 2 x 3 x 5 x 6.
Тогда произведение трех определяющих контрастов равно
1= x 1 x 4 x 5 x 6.
Чтобы полностью охарактеризовать разрешающую способность данной 1/8-реплики, запишем обобщающий определяющий контраст:
1= x 1 x 2 x 3 x 4= x 1 x 2 x 5= x 1 x 3 x 6= x 3 x 4 x 5= x 2 x 4 x 6= x 2 x 3 x 5 x 6= x 1 x 4 x 5 x 6.
Получается следующая система смешивания (эффекты выше второго порядка опущены):
x 1 = x 2 x 5= x 3 x 6= x 2 x 3 x 4= x 4 x 5 x 6 b1= β 1 + β 25 + β 36 + β 234+ β 456;
x 2 = x 1 x 5= x 4 x 6= x 1 x 3 x 4= x 3 x 5 x 6 b2= β 2 + β 15 + β 46 + β 134+ β 356;
x 3 = x 1 x 6= x 4 x 5= x 1 x 2 x 4= x 2 x 5 x 6 b3= β 3 + β 16 + β 45 + β 124+ β 256;
x 4 = x 3 x 5= x 2 x 6= x 1 x 2 x 3= x 1 x 5 x 6 b4= β 4 + β 35 + β 26 + β 123+ β 156;
x 5 = x 1 x 2= x 3 x 4= x 2 x 3 x 6= x 1 x 4 x 6 b5= β 5 + β 12 + β 34 + β 236+ β 146;
x 6 = x 1 x 3= x 2 x 4= x 2 x 3 x 5= x 1 x 4 x 5 b6= β 6 + β 13 + β 24 + β 235+ β 145.
Тогда уравнение регрессии будет иметь вид:
y = b0 + b 1x1 + b2x2 + b3x3 + b4x4 + b5x5+ b6x6,
и число степеней свободы равно нулю.
Рассмотрим пример 1/16-реплики от 27-4. 1/16 часть от полного факторного эксперимента 27-4 дает возможность сократить число опытов до 8 вместо 128.
Выберем следующие генерирующие соотношения:
x 4 = x 1 x 2, x 5 = x 1 x 3, x 6 = x 2 x 3, x 7 = x 1 x 2 x 3.
Для них имеем следующие определяющие контрасты:
1= x 1 x 2 x 4, 1= x 1 x 3 x 5, 1 = x 2 x 3 x 6, 1= x 1 x 2 x 3 x 7.
В результате попарного перемножения исходных контрастов, затем – умножения по три и по четыре получим обобщающий определяющий контраст вида:
1= x 1 x 2 x 4= x 1 x 3 x 5 = x 2 x 3 x 6= x 1 x 2 x 3 x 7= x 2 x 3 x 4 x 5= x 1 x 3 x 4 x 6 = x 3 x 4 x 7= x 1 x 2 x 5 x 6= =x 2 x 5 x 7= x 1 x 6 x 7 = x 4 x 5 x 6= x 1 x 4 x 5 x 7 =x 2 x 4 x 6 x 7= x 3 x 5 x 6 x 7 = x 1 x 2 x 3 x 4 x 5 x 6 x 7.
Если всеми коэффициентами взаимодействия, начиная с тройных, можно пренебречь, то коэффициенты будут совместными оценками:
x 1 = x 2 x 4= x 3 x 5= x 6 x 7 b1= β 1 + β 24 + β 35 + β 67;
x 2 = x 1 x 4= x 3 x 6= x 5 x 7 b2= β 2 + β 14 + β 36 + β 57;
x 3 = x 1 x 5= x 2 x 6= x 4 x 7 b3= β 3 + β 15 + β 26 + β 47;
x 4 = x 1 x 2= x 5 x 6= x 3 x 7 b4= β 4 + β 12 + β 56 + β 37;
x 5 = x 1 x 3= x 4 x 6= x 2 x 7 b5= β 5 + β 13 + β 46 + β 27;
x 6 = x 2 x 3= x 4 x 5= x 1 x 7 b6= β 6 + β 23 + β 45 + β 17;
x 7 = x 3 x 4= x 2 x 5= x 1 x 6 b7= β 7 + β 34 + β 25 + β 16.
Разрешающая способность такой реплики чрезвычайно мала, так как каждый линейный эффект определяется совместно с тремя парными взаимодействиями. Такой репликой можно пользоваться только в том случае, если все парные взаимодействия равны нулю. Матрицу планирования для этой реплики можно получить из первой реплики, изменив в ней все знаки на обратные. Такая реплика задается генерирующими соотношениями:
x 4 = - x 1 x 2, x 5 =- x 1 x 3, x 6 = - x 2 x 3, x 7 =- x 1 x 2 x 3.
В обобщающем определяющем контрасте все тройные произведения оказываются со знаком минус, а, следовательно, в совместных оценках для линейных эффектов не будет парных взаимодействий со знаком плюс. Усредняя результаты вычислений для таких двух реплик, можно получить раздельные оценки для всех линейных эффектов. Таким образом, экспериментатор должен сам установить, какие несмещенные оценки его интересуют, и какой дробности реплик допускается использовать для получения оценок.
С ростом числа факторов увеличивается дробность реплик и усложняется система смешивания. Предельное число факторов для восьми опытов – семь. В этом случае оценивается восемь коэффициентов линейного уравнения:
y = b 0 + b 1x1 + b 2x2 + b 3x3 + b 4x4 + b 5x5+ b 6x6+ b 7 x7,
и число степеней свободы равно нулю.
При числе факторов от 9 до 15 приходится ставить 16 опытов. При построении дробных планов для числа факторов от 16 до 31 необходимо ставить 32 опыта, а для числа факторов от 32 до 63 необходимо 64 опыта и т. д. (табл. 5.2). План с предельным числом факторов для данного числа опытов и заданной модели называется насыщенным. В этом случае число опытов равно числу оцениваемых коэффициентов. Все рекомендации для выбора системы смешивания аналогичны рассмотренным выше примерам.
При ДФЭ стандартизация масштабов факторов, порядок постановки опытов, проверка воспроизводимости опытов, расчет оценок коэффициентов регрессионного уравнения и проверка их статистической значимости, проверка адекватности полученной математической модели производится так же, как и при ПФЭ. Однако необходимо учитывать, что для насыщенного и сверхнасыщенного экспериментов невозможна проверка адекватности ММ, так как для нее уже не остается степеней свободы.
Методические рекомендации
1. В соответствии с индивидуальным заданием необходимо перейти к стандартизированному масштабу факторов, составить матрицу планирования ДФЭ, используя результаты лабораторной работы №4, заменив столбцы взаимодействия новыми факторами, рандомизировать опыты.
2. Провести ДЭФ.
3. Проверить воспроизводимость опытов. Если дисперсии неоднородны, повторить эксперимент.
4. Рассчитать оценки коэффициентов регрессионного уравнения.
5. Проверить статистическую значимость коэффициентов регрессии.
6. Проверить адекватность полученной математической модели.
7. Записать полученное уравнение регрессии и сделать вывод о влияние исследуемых факторов на качество продукции (параметр оптимизации).
Рассмотрим пример выполнения задания. Продолжим рассмотрение примера лабораторной работы №4 для ПФЭ. Воспользовавшись информацией, что взаимодействия факторов x1x2 и x1x3 оказались статистически незначимыми. Исследуем влияние на качество комплексных текстильных материалов дополнительных факторов: пористость мате-риалов и количество адгезива, и поставим для этой цели ДФЭ типа 25-2.
Условия проведения опытов сведем в табл. 5.5. Факторы x1, x2, x3 остаются такими же, как в таблице 4.4 (см. лаб. работу №4), а для факторов x4 и x5 генераторами плана выберем взаимодействия и x4 = x1x2 и x5 = x1x3 (табл. 5.6).
По формуле Хi = (xi - xoi) / dxi, где i = 1, 2, …, n; dxi – масштаб по оси Хi. Величину Хi называют кодированной переменной. Для каждого фактора выбираются два уровня – верхний xi max и нижний xi min, на которых фактор варьируется. Половина разности между верхним и нижним уровнями является интервалом варьирования dxi.
Таблица 5.5. Основные характеристики плана эксперимента
| Интервалы варьирования факторов | Факторы | ||||
| Х1 = Т, температура, оС | Х2 = τ, время, сек | Х3=Р, давление, 10-2 МПа | Х4=П, пористость материалов, % | Х5=Мад, количество адгезива, г/м2 | |
| Х10 | |||||
| dxi | |||||
| xi max | |||||
| xi min |
Выбираем масштаб и положение осей координат таким образом, чтобы Хi min соответствовало (–1), а Xi max (+1).
Поставим серию из трех опытов в точках: Т=(130±30) оС, τ= (30±20) сек, Р=(5±2) 10-2 МПа, П= (40±30) %, Мад =(20±10) г/м2.
Тогда определяющие контрасты будут соответственно 1= x1x2x4 и 1= x1x3x5, и их произведение 1= x2x3x4x5, а обобщающий определяющий контраст 1 = x1x2x4 = x1x3x5 = x2x3x4x5.
Найдем смешанность оценок:
x 1 = x 2 x 4= x 3 x 5= x 1 x 2 x 3 x 4 x 5 b1= β 1 + β 24 + β 35 + β 12345= β 1 + β 24 + β 35;
x 2 = x 1 x 4= x1x2x 3 x 5= x 3 x 4 x 5 b2= β 2 + β 14 + β 1235 + β 345= β 2 + β 14;
x 3 = x1x2 x3x4 = x1x5 = x2x4x5 b3= β 3 + β 1234 + β 15 + β 245= β 3 + β 15;
x 4 = x1x2 = x1x3 x4x5 = x2x3x5 b4= β 4 + β 12 + β 1345 + β 235= β 4 + β 12;
x 5 = x1x2x4 x5 = x1x3 = x2x3x4 b5= β 5 + β 1245 + β 13 + β 234= β 5 + β 13;
x 2 x3 = x1x3x4 = x1x2x5 = x4x5 b23= β 23 + β 134 + β 125 + β 45= β 23 + β 45;
x1x2x3 = x3x4 = x2x5 = x1x4x5 b123= β 123 + β 34 + β 25 + β 145= β 34 + β 25.
Учитывая, что тройными и более взаимодействиями β 12345; β 1235; β 345; β1234; β245; β 1345; β 1245; β 235; β 234; β 134; β 125; β 123; β 145, вследствие их незначительности можно пренебречь. В этом случае раздельными оценками будут b1,b2, b3, b4.
Тогда уравнение регрессии будет иметь вид:
y = b0 + b 1x1 + b2x2 + b3x3 + b4x4 + b5x5+ b23x2x3+ b123x1x2x3,(5.5)
и число степеней свободы равно нулю, так как число коэффициентов регресс равно число опытов в эксперименте.
Число опытов с 32 сократилось до 8. После составления матрицы планирования ДФЭ 25-2, 1/4 – реплики от ПФЭ 23, и проведения рандомизированных опытов сведем полученные результаты в таблицу 5.6.
Таблица 5.6. Дробный факторный плантипа 25-2.
| № точки факторного пространства (Номер опыта), N | х1 | х2 | х3 | х4 (х1х2) | х5 (х1х3) | х2х3 | х1х2х3 | у11 | у12 | у13 | ỹ | Диспер-сия, SУ2 | Gр | ΣS2в |
| 1, (4), (2) | - | - | - | + | + | + | - | 4,5 | 4,9 | 4,2 | 4,53 | 0,123 | 0,256 | 1,454 |
| 2, (2), (4) | + | - | - | - | - | + | + | 5,9 | 6,3 | 6,5 | 6,23 | 0,09 | ||
| 3, (1), (6) | - | + | - | - | + | - | + | 5,2 | 5,7 | 5,9 | 5,6 | 0,13 | ||
| 4, (7), (8) | + | + | - | + | - | - | - | 12,4 | 12,1 | 12,5 | 0,21 | |||
| 5, (8), (1) | - | - | + | + | - | - | + | 6,2 | 6,6 | 6,9 | 6,56 | 0,123 | ||
| 6, (3), (7) | + | - | + | - | + | - | - | 10,4 | 10,7 | 9,8 | 10,63 | 0,373 | ||
| 7, (5), (3) | - | + | + | - | - | + | - | 8,1 | 8,9 | 9,0 | 8,66 | 0,232 | ||
| 8, (6), (5) | + | + | + | + | + | + | + | 5,6 | 5,8 | 6,4 | 5,93 | 0,173 |
Примечание: в скобках указаны номера рандомизированной последовательности в трех сериях опытов.
Из анализа матрицы планирования видно, что ДФЭ обладает свойствами:
ортогональности. Сумма парных произведений элементов любых двух различных столбцов равна нулю. В частности, для простых переменных

где N- число опытов, i, j, m – номера факторов (переменных);
симметричности относительно центра эксперимента. Сумма всех элементов любого столбца, за исключением первого, равна нулю:

нормированности. Сумма квадратов элементов любого столбца равна числу опытов, так для i -й переменной
 .
.
Проведем статистическую обработку полученных результатов. Для проверки по критерию Кохрена воспроизводимости опытов для принятого уровня значимости a=0,05 вычислим в каждой точке факторного пространства среднее значение  (по формуле 4.7) и дисперсию
(по формуле 4.7) и дисперсию  (по формуле 4.8) исследуемого параметра. Полученные результаты также заносим в таблицу 5.6.
(по формуле 4.8) исследуемого параметра. Полученные результаты также заносим в таблицу 5.6.
Рассчитаем оценки коэффициентов регрессионного уравнения (5.5) и проверим их статистическую значимость по критерию Стьюдента (формула 4.15) при α =0,05. По критерию Фишера (4.17) проверим адекватность линейной, а затем нелинейной ММ при α =0,05.
Расчетное значение коэффициента Кохрена сравнивается с табличным значением Gтабл – критерия, которое выбирается из таблиц для принятого уровня значимости a=0,05 и для чисел степени свободы соответственно числителя (по горизонтали) f1 и знаменателя f2 (по вертикали).
f1=m –1=3-1=2; f2 =N =8, где п – число параллельных опытов, N -число опытов в эксперименте, (m –1) – число степеней свободы, равное количеству параллельных опытов минус единица, т.к. одна степень свободы использована для вычисления среднего.
В соответствии с таблицей Gтабл=0,816; Gт>Gp, т.е. условие выполняется. Следовательно, опыты считаются воспроизводимыми, а оценки дисперсий sу2 - однородными.
Коэффициенты регрессии рассчитываем по формулам 4.11.








Уравнение регрессии описывающее поверхность отклика имеет вид:
y = 7,33 + 1,24x1 + 0,59x2 + 0,37x3 - 0,2x4 – 1,4x5 – 1,24x2x3- 1,5 x1x2 x3
Определяем дисперсию воспроизводимости параллельных опытов S2 воспр:
S2 воспр =ΣS2воспр/ 8 = 1,454/8 = 0,182.
Вычисляем дисперсию коэффициентов регрессии S b:
S b 2 = S2 воспр / N, где N - число опытов в эксперименте;
S b 2 =0,182/8·=0,022, откуда S b =0,15.
Статистическую значимость коэффициентов регрессии проверяем по критерию Стьюдента t. Коэффициенты регрессии значимы, если |b|≥ S b t. Рассчитаем критерий Стьюдента tр = |bi| / S b для всех коэффициентов регрессии: b0 =7,33; b1 =1,24; b2 =0,59; b3 = 0,37; b4 = -0,2; b5 = -1,4; b23 =-1,24; b123 =-1,5.
Для доверительной вероятности Р=0,95, при числе степеней свободы f=N(п-1) = 8(3-1)=16, значение критерия Стьюдента t=2,1190 (приложение 2). t0 = |b0| / S b = 7,33/0,15=48,86>2,119;
t1 = |b1| / S b = 1,24/0,15=8,26>2,119;
t2 = |b2| / S b = 0,59/0,15=3,93>2,119;
t3 = |b3| / S b = 0,37/0,15=2,46>2,119;
t4 = |b4| / S b = 0,2/0,15=1,33<2,119;
t5 = |b5| / S b = 1,4/0,15=9,33>2,119;
t23 = |b23| / S b = 1,24/0,15=8,26>2,119;
t123 = |b123| / S b = 1,5/0,15=10>2,119;
Отсюда видно, что коэффициент регрессии b4 незначим.
Получили математическое описание процесса в виде уравнения регрессии:
Линейная ММ: y=7,33+1,24x1 + 0,59x2 + 0,37x3 – 1,4x5 (5.6)
Нелинейная: y=7,33+1,24x1+0,59x2+0,37x3–1,4x5 –1,24x2x3-1,5x1x2 x3 (5.7)
Проверка адекватности уравнения регрессии исследуемому объекту проводим по критерию Фишера. Fp = S2 ад / S2 воспр
Вычисляем оценку дисперсности адекватности:
 = Σ(ỹi эк - ỹi р)2 / (N – В), где N – число опытов в эксперименте; В – число членов уравнения регрессии.
= Σ(ỹi эк - ỹi р)2 / (N – В), где N – число опытов в эксперименте; В – число членов уравнения регрессии.
Определяем расчетное значение ỹi р.
y1р = 7,33 + 1,24(-1) + 0,59(-1) +0,37(-1)-1,4(+1)-1,24 (+1)-1,5(-1) = 3,99
y2р = 7,33 + 1,24(+1) + 0,59(-1) +0,37(-1)-1,4(-1)-1,24 (+1)-1,5(+1) = 6,27
y3р = 7,33 + 1,24(-1) + 0,59(+1) +0,37(-1)-1,4(+1)-1,24 (-1)-1,5(+1) = 4,65
y4р = 7,33 + 1,24(+1) + 0,59(+1) +0,37(-1)-1,4(-1)-1,24 (-1)-1,5(-1) = 12,93
y5р = 7,33 + 1,24(-1) + 0,59(-1) +0,37(+1)-1,4(-1)-1,24 (-1)-1,5(+1) = 7,01
y6р = 7,33 + 1,24(+1) + 0,59(-1) +0,37(+1)-1,4(+1)-1,24 (-1)-1,5(-1) = 9,69
y7р = 7,33 + 1,24(-1) + 0,59(+1) +0,37(+1)-1,4(-1)-1,24 (+1)-1,5(-1) = 8,71
y8р




