Должны содержать заключение о значимости коэффициентов регрессии, уравнение регрессии и заключение о его адекватности поверхности отклика исследуемого объекта.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что собой представляет математическое описание объекта?
2. Какие принципы лежат в основе составления плана двухфакторного эксперимента?
3. Какими свойствами обладает план полного двухфакторного эксперимента?
4. Как определяют коэффициенты уравнения регрессии?
5. Что характеризует и как определяется значимость коэффициентов регрессии?
6. Как и для чего проверяют адекватность уравнения регрессии исследуемому объекту?
Лабораторная работа №4
ПОСТРОЕНИЕ И АНАЛИЗ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПОЛНОГО ФАКТОРНОГО ЭКСПЕРИМЕНТА ТИПА 2k
Цель работы: изучение основ теории планирования эксперимента, приобретение навыков построения и анализа матрицы планирования и математической модели в виде уравнения регрессии многофакторного эксперимента.
Задание: получить адекватное уравнение регрессии, описывающее влияние факторов на качество конкретной продукции в соответствии с заданием.
Основные сведения
Особенность многофакторного эксперимента (МФЭ) состоит в том, что он предусматривает одновременное варьирование многими факторами хin, влияющими на параметр у (в отличие от традиционного эксперимента, когда факторы изучаются, т.е. варьируются, по одному при фиксированных значениях других факторов).
Цель многофакторного эксперимента – оценка влияния факторов с учетом их взаимодействий (взаимного влияния) и получение новой информации, которую не дает традиционный эксперимент. Результаты МФЭ представляют в виде многофакторной модели, которая может быть использована для анализа факторов: по степени и направлению их влияния; для оптимизации исследуемого объекта; для выборки рекомендаций по определению допусков назначения факторов, при которых обеспечивается нахождение значений выходной величины в требуемом диапазоне.
Если в МФЭ использованы все возможные комбинации уровней факторов k, то такой эксперимент называется полным факторным экспериментом. Полный факторный эксперимент (ПФЭ) включает в себя 2k опытов. Зависимость количества взаимодействий различного порядка от числа факторов ПФЭ приведена в табл. 4.1. Полное число всех возможных эффектов, включая и b0, равно числу опытов ПФЭ.
Таблица 4.1. Взаимосвязь характеристик ПФЭ
| Число факторов, k | Число линейных эффектов (коэффициентов) | Число опытов, N=2k | Число и порядок взаимо-действий (коэффициентов) | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
Эффект взаимодействия x 1 x 2 x 3 получается перемножением всех трех столбцов и называется эффектом взаимодействия второго порядка. Эффект взаимодействия двух факторов называется эффектом взаимодействия первого порядка. Вообще, эффект взаимодействия максимального порядка в полном факторном эксперименте имеет порядок, на единицу меньший числа факторов.
Полное число всех возможных эффектов, включая b 0, линейные эффекты и взаимодействия всех порядков, равно числу опытов полного факторного эксперимента. Чтобы найти число возможных взаимодействий (Cnk) некоторого порядка, можно воспользоваться обычной формулой числа сочетаний:
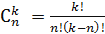, (4.1)
где k – число факторов, n – число элементов во взаимодействии. Так, для плана 23 число взаимодействий взаимодействия первого порядка равно трем, а для плана 24 шести:
.
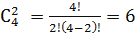Физический смысл эффекта взаимодействия заключается в следующем: например, пусть на процесс дублирования влияют два фактора: температура и время. В области низких температур увеличение времени повышает прочность клеевого соединения. При переходе в область высоких температур, напротив, необходимо уменьшать время дублирования, чтобы получить высокую прочность клеевого соединения. Это и есть проявление эффекта взаимодействия.
Рассмотрим составление плана ПФЭ с тремя независимыми переменными Х 1 , Х 2 и Х 3. Нулевой фактор Х 0 вводится для удобства расчета свободного члена b0 уравнения регрессии. Условия проведения опытов полного трехфакторного 23 эксперимента приведены в табл. 4.2.
Таблица 4.2. План полный трехфакторный эксперимент
| номер опыта, N | Матрица планирования | Вектор результатов | |||||||
| Факторы, Хi | Факторы взаимодействия хij хjm | y | |||||||
| Х 0 | Х 1 | Х 2 | Х 3 | Х 1 Х 2 | Х 1 Х 3 | Х 2 Х 3 | Х 1 Х 2 Х 3 | ||
| 1 | 2 | 6 | 7 | 8 | 9 | 10 | |||
| + | – | – | – | + | + | + | – | y 1 | |
| + | – | – | + | + | – | – | + | y 2 | |
| + | – | + | – | – | + | – | + | y 3 | |
| + | – | + | + | – | – | + | – | y 4 | |
| + | + | – | – | – | – | + | + | y 5 | |
| + | + | – | + | – | + | – | – | y 6 | |
| + | + | + | – | + | – | – | – | y 7 | |
| + | + | + | + | + | + | + | + | y 8 |
Существует несколько способов построения матриц планирования. Например, в столбце переменной Х 3 знаки меняются поочередно, в столбце переменной Х 2 – чередуются через два элемента, для переменной Х 1 – знаки меняются через четыре элемента. Аналогично строится матрица для любого количества переменных, порядок перечисления переменных не играет роли. Столбцы факторов взаимодействия получают произведением переменных, т.е. вычисляются путем простого перемножения значений элементов соответствующих столбцов.
Эти опыты соответствуют в факторном пространстве вершинам куба с центром в начале координат (рис. 4.1). Если k >3, то фигура, задающая в пространстве область определения параметра оптимизации, называется гиперкубом. По 8-ми точкам такого плана строится модель зависимости:
|
| Рис. 4.1. Геометрическая интерпретация трехфакторного эксперимента |
y= f(x1, x2, …, x8),
по которой можно вычислить (у) при любых (х) без постановки опытов, поскольку эту зависимость представ-ляют в виде разложения в ряд Тейлора (4.2) в точке, соответствую-щей центру эксперимента.
y = b 0 +b1Х1 + b 2Х2 + b 3Х3 + b 12Х1Х2 + +b13Х1Х3+b23Х2Х3+b 123 Х1Х2 Х3 (4.2)
Из анализа матрицы планирования легко видеть, что полный факторный эксперимент обладает свойствами:
ортогональности. Сумма парных произведений элементов любых двух различных столбцов равна нулю. В частности, для простых переменных:
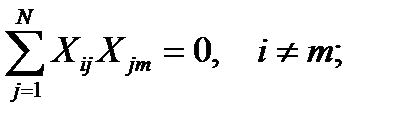
где N- число опытов, i, j, m – номера факторов (переменных);
симметричности относительно центра эксперимента. Сумма всех элементов любого столбца, за исключением первого, равна нулю:
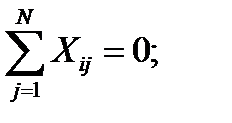
нормированности. Сумма квадратов элементов любого столбца равна числу опытов, так для i -й переменной
.
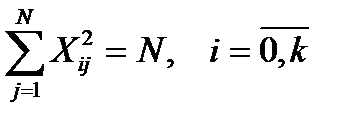Ортогональность матрицы планирования позволяет получить независимые друг от друга оценки коэффициентов. Это означает, что величина любого коэффициента не зависит от того, какие величины имеют другие коэффициенты. Однако сформулированные выше утверждения справедливы лишь в том случае, если модель включает только линейные эффекты и эффекты взаимодействия.
Для облегчения записи условий эксперимента и упрощения его анализа, от исходных переменных х переходим к их кодированным значениям (безразмерным единицам) Хi.
Хi = (xi - xoi) / ∆ xi (4.3)
где i = 1, 2, …, n; ∆ xi – шаг варьирования или масштаб по оси Хi; xi0 – центр варьирования переменных; Хi называют кодированной переменной.
Для каждого фактора выбираются два уровня – верхний xi max и нижний xi min, на которых фактор варьируется. Половина разности между верхним и нижним уровнями называется интервалом варьирования dxi. Интервал варьирования должен быть больше погрешности измерения уровня фактора, а верхний и нижний уровни факторов не должны выходить за область его определения. Интервал варьирования обычно составляет 5-15% от области определения.
Рассмотрим пример полного трехфакторного эксперимента. Необходимо провести оптимизацию процесса производства комплексных текстильных материалов, получаемых по клеевой технологией, с целью обеспечение высокое качество продукции. Переменными факторами, выбираем: х1 – температура прессования, оС; х2 - продолжительность, сек; х3 – давление прессующих поверхностей, 10-2 МПа. В качестве параметра оптимизации у, характеризующего качество комплексных полотен, выбираем прочность при расслаивании клеевого соединения двух составляющих его слоев, Н/см. В соответствии с нормативными требованиями она должна быть не менее 5 Н/см.
Сначала задаемся областью варьирования факторов xi max и xi min. Затем находим центр варьирования по формуле:
xi0 = (xi max + xi min) / 2; (4.4)
Вычисляем интервал изменения фактора:
dxi = хi 0 – хi min = хi max - хi 0. (4.5)
Находим нормированное значение хiн для каждого фактора:
хiн = (хi0 – хi0) / dxi (4.6)
x10 = (x1max + x1min) / 2 = (160+100)/2 = 130; dx1 =130-100=30
x20 = (x2 max + x2min) / 2= (50+10) / 2 = 30; dx2 =30-10=20
x30 = (x3 max + x3 min) / 2; (7+3) / 2 =5; dx3 = 5-3=2
Результаты заносим в таблицу 4.3.
Таблица 4.3. Основные характеристики плана эксперимента
| Интервалы варьирования факторов | Факторы | ||
| х1 = Т, температура, оС | х2 = τ, время, сек | х3=Р, давление, 10-2 МПа | |
| Х10 | |||
| dxi | |||
| xi max | |||
| xi min |
Выбираем масштаб и положение осей координат таким образом, чтобы хi min соответствовало (–1), а хi max (+1).
Поставим серию трех опытов в точках: Т=(130±30) оС, τ= (30±20) сек, Р=(5±2) 10-2 МПа. Составляем матрицу планирования и заносим результаты предварительного эксперимента в таблицу 4.4.
Таблица 4.4. Полный трехфакторный эксперимент
| № точки факторного пространства (Номер опыта), N | х1 | х2 | х3 | х1х2 | х1х3 | х2х3 | х1х2х3 | у1 | у2 | У3 | ỹ | Sу2 | Gр | ΣSу2 |
| 1, (2), (3) | - | - | - | + | + | + | - | 3,5 | 3,9 | 3,8 | 0,07 | 0,203 | 1,255 | |
| 2, (4), (1) | + | - | - | - | - | + | + | 5,5 | 5,9 | 6,5 | 0,21 | |||
| 3, (1), (4) | - | + | - | - | + | - | + | 5,5 | 5,8 | 5,4 | 0,165 | |||
| 4, (3), (2) | + | + | - | + | - | - | - | 12,6 | 12,5 | 0,255 | ||||
| 5, (8), (6) | - | - | + | + | - | - | + | 4,6 | 4,4 | 4,3 | 0,09 | |||
| 6, (7), (8) | + | - | + | - | + | - | - | 10,2 | 9,6 | 9,9 | 0,09 | |||
| 7, (6), (5) | - | + | + | - | - | + | - | 7,9 | 8,5 | 8,8 | 8,4 | 0,21 | ||
| 8, (5), (7) | + | + | + | + | + | + | + | 5,4 | 5,9 | 6,2 | 5,8 | 0,165 |
Примечание: в скобках указаны номера рандомизированной последовательности в трех сериях опытов.
Рассчитываем среднее арифметическое значение параллельных опытов функции отклика ỹ по формуле (4.7), результаты заносим в табл. 4.4:
где m – число параллельных опытов.
Для уменьшения влияния внешней среды и неконтролируемых факторов внутри каждой серии опытов точки факторного пространства обходят случайным образом, т.е. рандомизируют последовательность опытов. Сущность рандомизации состоит в следующем. Любое экспериментальное исследование проводится, как правило, в условиях действия систематических ошибок и факторов, которые трудно поддаются учету и контролю. Концепция рандомизации предлагает, что план эксперимента составляется таким образом, чтобы рандомизировать, то есть сделать случайными в пространстве и во времени, систематически действующие мешающие факторы. Тогда эти факторы можно рассматривать как случайные величины и, следовательно, учесть статистически их влияние в значении ошибки эксперимента. Иными словами, в противоположность традиционному подходу к эксперименту со стремлением стабилизировать мешающие факторы, рандомизация внесла концепцию «случая» в эксперимент. При этом опыты в одной точке проводят не подряд, а обходят все точки в первой серии опытов, затем во второй, и так далее до m -ого опыта. Рандомизацию опытов можно провести с помощью генератора (таблицы) случайных чисел (см. приложение 3).
Определяем отклонения от среднего арифметического значения для каждого результата yj и по формуле (4.8) рассчитываем оценку дисперсии, результаты заносим в табл. 4.4:
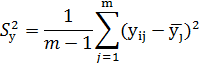
(4.8)
S2{y11}= [(3,5–3,8)2 +(4–3,8)2 + (3,9–3,8)2]/2 = 0,07
………………………..
S2{y18}= [(5,4–5,8)2 +(5,9–5,8)2 + (6,2–5,8)2]/2 = 0,165
Проведем проверку однородности оценок дисперсий по критерию Кохренарассчитаем по формуле (4.9), результаты заносим в табл. 4.4:
(4.9)
Gp = 0,255/1,255 = 0,203.
Расчетное значение коэффициента Кохрена сравнивается с табличным значением Gтабл – критерия (приложение 1), которое выбирается из таблиц для принятого уровня значимости a=0,05 и для чисел степени свободы соответственно числителя (по горизонтали) f1 и знаменателя f2 (по вертикали).
f1= n –1=2; f2 = N =8, где п – число параллельных опытов, N-число опытов в эксперименте.
В соответствии с таблицей Gтабл=0,816; Gтабл>Gp, т.е. условие выполняется. Следовательно, опыты считаются воспроизводимыми, а оценки дисперсий sу2 - однородными.
Уравнение регрессии описывающее поверхность отклика имеет общий вид:
y=b 0 +b1Х1+b2Х2+b3Х3+b12Х1Х2+b13Х1Х3+b23Х2Х3+b123 Х1Х2 Х3 (4.10)
Расчет оценок коэффициентов уравнения регрессии производится по методу наименьших квадратов, при этом минимизируется сумма квадратов отклонений между экспериментальными значениями исследуемого параметра и значениями, вычисленными для тех же точек факторного пространства по уравнению регрессии. Благодаря предварительной стандартизации масштаба факторов и ортогональности МП, расчет оценок коэффициентов регрессии в ПФЭ превращается в простую арифметическую процедуру. Коэффициенты регрессии рассчитывали по формулам:
; 
; 
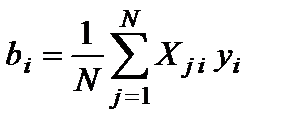(4.11)
где коэффициенты bi характеризуют силу влияния каждого из факторов, а их знак (-) направление влияния факторов. То же относится и коэффициентам bij, характеризующим силу и направление влияния взаимодействия факторов.
Благодаря оптимальным свойствам плана 2k все коэффициенты его полиномиальной модели оцениваются независимо друг от друга с одинаковыми минимальными дисперсиями и максимальной точностью.
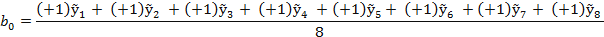
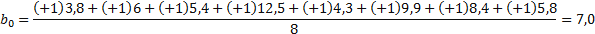
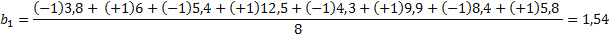
По аналогии находим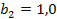 
; 
; 
; 
; 
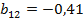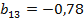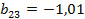
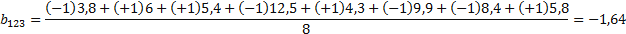
Тогда уравнение регрессии исследуемого параметра оптимизации имеет вид:
y =7+1,54Х1 +1,0Х2 +0,85Х3 -0,41Х1Х2 -0,78Х1Х3-1,01Х2Х3-1,64 Х1Х2 Х3 (4.12)
После получения уравнения производится статистический анализ значимости вычисленных коэффициентов и проверка адекватности уравнения. С этой целью вычисляют построчные дисперсии в каждом опыте плана, характеризующие изменчивость результатов в опытах плана относительно их средних значений.
Критерии адекватности и погрешности эксперимента вычислим по формулам:
-дисперсия воспроизводимости параллельных опытов, характеризует погрешность наблюдений:
, (4.13)
- проверка адекватности воспроизводимости:
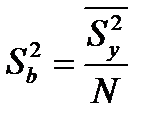(4.14)
Sb2 = 1,255 / 8= 0,156.
Ошибку в определении коэффициентов регрессии вычислим, извлекая корень из адекватности воспроизводимости S b 2 , откуда S b =0,394.
Гипотизу о статистической значимости (отличии от нуля) коэффициентов регрессии проверяют по критерию Стьюдента t. Коэффициенты регрессии значимы, если
(4.15)
Вычислим доверительный интервал для коэффициентов модели, как произведение ошибки в определении коэффициентов S b, умноженное на табличное значение критерия Стьюдента t (значение критерия Стьюдента находим по таблице приложения 2). Для доверительной вероятности Р=0,95, при числе степеней свободы f=N(т-1) = 8(3-1)=16, значение критерия Стьюдента t=2,1190; п – число параллельных опытов, проведенных при одинаковых условиях.
S bt = 0,394 ·2,119 = 0,835
Для оценки значимости коэффициентов регрессии рассмотрим следующие соотношения:
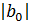= 7 > S bt; 
= 1,54 > S bt; 
= 1 > S bt;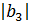 
= 0,85 > S bt;
= 0,41 < S bt; 
= 0,78 < S bt; 
= 1,01 > S bt; 
= 1,64 > S bt;
Отсюда видно, что коэффициенты регрессии b12 и b13 незначимы.
Отбросим все статистически незначимые коэффициенты, получим математическое описание процесса в виде линейного уравнения регрессии:
y = 7 + 1,54Х1 + 1,0Х2 + 0,85Х3 -1,01Х2Х3-1,64 Х1Х2 Х3 (4.16)
Уравнение, включающее только оставшиеся значимые коэффициенты, проверим на адекватность. Проведем проверку адекватности уравнения регрессии исследуемому объекту по критерию Фишера.
, (4.17)
где 
–дисперсия адекватности, 
- дисперсия воспроизводимости.
Для оценки дисперсии адекватности необходимо оценить, насколько отличаются средние значения экспериментального ỹiэ выходного параметра, полученного в точках факторного пространства, и значения yiр, полученного из уравнения регрессии в тех же точках факторного пространства. Вычисляем оценку дисперсности адекватности:
, (4.18)
где N - общее число опытов ПФЭ; В- число коэффициентов регрессии искомого уравнения; уjэ, уjр - экспериментальное и расчетное значение функции отклика в j-м опыте.
y1р = 7 + 1,54(-1) + 1,0(-1) +0,85(-1)-1,01(+1)-1,64 (-1) = 4,24
y2р = 7 + 1,54(+1) + 1,0(-1) +0,85(-1)-1,01(+1)-1,64 (+1) =4,05
y3р = 4,98; y4р = 8,26; y5р = 4,68; y6р = 11,04; y7р = 7,94
y8р = 7 + 1,54(+1) + 1,0(+1) +0,85(+1)-1,01(+1)-1,64 (+1) =7,74
=[1/(8-6)] ·[(3,8-4,24)2+(6-4,05)2+(5,4-4,98)2+(12,5-8,26)2+ +(4,3-4,68)2+(9,9-11,04)2+(8,4-7,94)2+(5,8-7,74)2]=13,77
Произведем расчет F- критерия Фишера:
Fp= S2ад /S2ỹ. Fp = 13,77/1,255 =10,98
Найденное расчетным путем Fp сравнивают с табличным значением Fтабл (см. приложение 4), которое определяем при уровне значимости α =0,05 и числе степеней свободы fад (2)=N–В=8-6=2 и fв(1)=N(m-1)= =8(3-1)=16. Fтабл=19,37.
Если Fp< Fтабл, то полученная математическая модель с принятым уровнем статистической значимости q =0,05 адекватна экспериментальным данным. В рассматриваемом примере 
, 10,98<19,37.
Следовательно, уравнение регрессии:
y = 7 + 1,54Х1 + 1,0Х2 + 0,85Х3 -1,01Х2Х3-1,64 Х1Х2 Х3
является адекватным исследуемому объекту, при доверительной вероятности Р=0,95, и позволяет оптимизировать процесс производства комплексных текстильных материалов с целью обеспечения высокой прочности клеевого соединения его слоев.
Методические рекомендации
Из таблицы вариантов заданий (табл. 4.5) выбрать свой вариант в соответствии с последней цифрой номера Вашей зачетной книжки.
Задание. Вам надо доказать что производство способно выпускать продукцию, отвечающую требованиям технических регламентов. Требуется доказать, что установленные параметры процесса производства являются оптимальными, а выпускаемая продукция обладает высоким качеством и конкурентоспособностью.
Таблица 4.5. Варианты заданий
| Номер варианта, вид производства | Задания | |
| Область определения факторов | Область определения параметров | |
| №1. Производство костюмной полушерстяной ткани | Х1 – поверхностная плотность, г/м2; xi max - 350; xi min – 200. Х2 – содержание синтетических волокон, %; xi max - 80; xi min – 20. Х3 – крутка нитей, кр/м; xi max - 1800; xi min – 900. | У1 – разрывная нагрузка, даН; (ГОСТ 28000-2004. Не менее 39/29, основа/уток). У2 – стойкость к истиранию до дыры, тыс.циклов; (норматив не менее 4,5) |
| №2. Производство пальтовой чистошерстяной ткани | Х1 – поверхностная плотность, г/м2; xi max - 550; xi min – 350. Х2 – разрывная нагрузка нитей, сН/текс; xi max - 50; xi min – 20. Х3 – крутка нитей, кр/м; xi max - 600; xi min – 200. | У1 – разрывная нагрузка, даН; (ГОСТ 28000-2004. Не менее 28/24 основа/уток); У2 – стойкость к истиранию до дыры, тыс.циклов; (норматив не менее 4,0) |
| №3. Производство джинсовой ткани | Х1 – поверхностная плотность, г/м2; xi max - 350; xi min – 200. Х2 – крутка нитей, кр/м; xi max - 1200; xi min – 500. Х3 – содержание эластановой нити, %; xi max - 50; xi min – 25. | У1 – разрывная нагрузка, даН; (ГОСТ 21790-2005. Не менее 80/40, осн./уток). У2 – стойкость к истиранию до дыры, тыс.циклов; (норматив не менее 2,0) |
| №4. Производство полульняной костюмной ткани | Х1 – поверхностная плотность, г/м2; xi max - 250; xi min – 140. Х2 – содержание лавсановых волокон, %; xi max - 70; xi min – 20. Х3 – количество аппрета, %; xi max - 7,5; xi min – 1,5. | У1 – разрывная нагрузка, даН; (ГОСТ 21790-2005. Не менее 28/50, осн./уток) У2 – усадка, %; (Не более 6/4, основа/уток) |
| №5. Производство одежды из кожи | Х1 – масса шкурки, г/дм2; xi max - 290; xi min – 110. Х2 – предел прочности при растяже-нии, МПа;xi max - 35; xi min – 10. Х3 – устойчивость окраски к трению, балл; xi max - 5; xi min – 3. | У1 – срок эксплуатации, год; (Требования ГОСТ 31293-2005. Не менее 3 лет). У2 – износостойкость, %; (Не менее 80) |
| Окончание табл. 4.5 | ||
| №6. Производство верхних трикотажных полотен | Х1 – поверхностная плотность, г/м2; xi max - 650; xi min – 250. Х2 – разрывная нагрузка нитей, Н; xi max - 20; xi min – 8. Х3 – крутка нитей, кр/м; xi max - 900; xi min – 400. | У1 – разрывная нагрузка, даН; (норматив не менее 20/35, основа/уток). У2 – воздухопроницаемость, дм3/м2с; (не более 135). |
| №7. Производство тканепрошивных нетканых полотен | Х1 – поверхностная плотность, г/м2; xi max - 450; xi min – 150. Х2 – разрывная нагрузка основы, даН; xi max - 25; xi min – 10. Х3 – плотность прошивки, нитей на 50 мм. xi max - 40; xi min – 20. | У1 – разрывная нагрузка нетканого полотна, даН; (норматив не менее 20/15, основа/уток); У2 – усадка, %; не более 7,5. |
| №8. Производство плательно-костюмной ткани из натурального шелка | Х1 – поверхностная плотность, г/м2; xi max - 220; xi min – 100. Х2 – крутка нитей, кр/м; xi max -2000; xi min – 1000. Х3 – разрывная нагрузка нитей, сН/текс; xi max - 600; xi min – 300. | У1 – разрывная нагрузка, даН; (ГОСТ 20723-84, не менее 25/20, осн./уток); У2 – стойкость к истиранию до дыры, циклов; Не менее 150 (до 400). |
| №9 отделка хлопчатобумажных тканей | Х1 – Количество аппрета, г/м2; xi max - 8; xi min – 1,5. Х2 – температура раствора, оС; xi max - 50; xi min – 20. Х3 – содержание карбомола, %. xi max - 40; xi min – 10. | У1 – несминаемость, %; (норматив не менее 55). У2 – жесткость при изгибе, тыс. мкН·см2, (норматив не более 7). |
| №10 Процесс производства плащевых тканей | Х1 – количество полимерного покры-тия, г/м2; xi max - 30; xi min – 10. Х2 – температура сушки, оС; xi max - 110; xi min - 80 Х3 – поверхностная плотность осно-вы, г/м2; xi max - 300; xi min - 100 | У1 – водонепроницаемость, мм.вод.ст.; (Не менее 700). У2 – жесткость при изгибе, тыс. мкН·см2, (норматив не более 7) |
Порядок выполнения задания:
1. Перейти от физических величин к стандартизированному масштабу факторов;
2. Составить матрицу планирования для полного трехфакторного эксперимента с использованием дополнительного нулевого фактора (х 0):
3. Провести эксперимент, повторив 3 раз опыты во всех точках факторного пространства. Найти значения функции отклика у1 и у2;
4. Проверить воспроизводимость и однородность дисперсии опытов по критерию Кохрена;
5. Найти коэффициенты уравнения регрессии у1 и у2;
6. С помощью критерия Стьюдента оценить статистическую значимость коэффициентов регрессии;
7. Составить уравнение регрессии у1 и у2 в кодированном виде и проверить его адекватность с помощью критерия Фишера;
8. Провести анализ уравнения регрессии и исследуемых параметров оптимизации.
