1-есеп: Кеңістікте берілген қандай да бір АВСD квадраты мен одан тысқары бір жазықтықта жатқан N нүктесінің кескінін салу керек болсын.
Шешуі: Егер берілген жазықтық бейнелеу жазықтығымен беттессе немесе параллель болса, онда берілген квадрат өзгеріссіз бейнеленеді (73,а-сурет). Ал енді бейнелеу жазықтығы берілген жазықтықпен беттеспеген және параллель емес болатын жағдайын қарастырамыз.
Демек, берілген кескінді салу үшін бейнелеу жазықтығында кез келген А1В1С1D1 параллелограмын квадраттың кескіні ретінде саламыз. Енді N нүктесінің кескінін еркін сала алмаймыз (73,ә-сурет).
Өйткені 2-теоремаға сәйкес бейнелеу жазықтығында кескінделген үш базистік нүкте арқылы осы жазықтықтағы әрбір нүкте бір мәнді анықталған.
Олай болса, N нүктесінің кескінін салу үшін түпнұсқадан АN кесіндісі мен ВС кесіндісінің қиылысу нүктесі К, ВС және AN кесінділерін, қандай қатынаста бөлетіндігін анықтау қажет. Проекциялаудың және кескіндеудің 40 -қасиетіне сәйкес, А1В1С1D1 параллелограмының кескінінен В1К1:К1С1=ВК:КС қатынасы сақталатындай К1 нүктесін саламыз. А1К1 түзуін жүргізіп, осы түзуден, А1К1:К1N1=AК:КN қатынасы орындалатындай N1 нүктесі салынады. Алынған N1 нүктесі N нүктесінің кескіні болып табылады.
Квадратпен бір жазықтықта орналасқан нүктенің кескінін салу мәселесін анықтай отырып, квадратпен бір жазықтықта орналасқан кез келген фигураны кескіндеу процесін анықтадық. Яғни, квадраттың кескіні ретінде қандай да бір параллелограмм салынғаннан кейін, фигура кескіні еркін салынбай, оның негізгі нүктелерінің кескіні осы қарастырған тәсілге ұқсас салына отырып анықталады. Осы тұжырымды бекіту мақсатында бірнеше нақты мысалдарға тоқталамыз.
2-есеп: Кеңістікте бір жазықтықта орналасқан квадрат пен үшбұрыш берілген. Олардың кескінін салу керек.
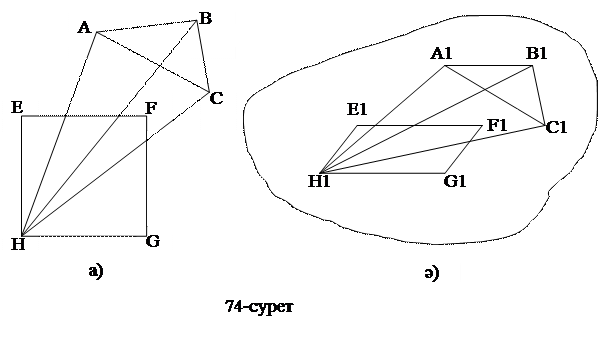Ол үшін бар болудың 1-теоремасының негізінде АВС үшбұрышының кескіні кез келген А1В1С1 үшбұрышы ретінде салынады. Ал EFGH квадратының төбелері жоғарыда қарастырылған әдіспен анықталып, E1F1G1H1 параллелограмы салынады (74-сурет).
Немесе осы кескінді орындау процесін керісінше орындауға болады. Яғни бірінші кезекте EFGH квадратының кескіні кез келген E1F1G1H1 параллелограмы ретінде салынады (квадрат кескіні кез келген параллелограмм болатындығы жоғарыда көрсетілген болатын). Олай болса, енді АВС үшбұрышының кескінін еркін орындай алмаймыз. Оның әрбір А1, В1, С1 төбелерінің кескінін жоғарыда келтірілген тәсіл бойынша салу керек.
3-есеп: Кеңістікте квадратқа іштей сызылған шеңбер берілген. Кескінін салу керек.
Берілген АВСD квадраты мен оған іштей сызылған шеңбердің (75,а-сурет) кескінін салу үшін, еркін түрдегі А1В1С1D1 параллелограмын АВСD квадратының кескіні ретінде аламыз (75,ә-сурет).
Ал квадратқа іштей сызылған шеңбердің кескінін салу үшін, оның өтетін бірнеше нүктесін анықтап алу қажет. Мектеп практикасында 6-8 нүктені анықтаумен шектелуге болады. Ол нүктелер түпнұсқадан (75,а-сурет) көріп отырғанымыздай шеңбердің квадратты жанау нүктелері, яғни квадрат қабырғаларының орталары. Бұл нүктелердің кескіндері сәйкесінше А1В1 қабырғасының ортасы Е1, т.с.с. В1С1 ортасы L1, C1D1 ортасы F1, A1D1 ортасы N1 болады. Ал басқа нүктелерді анықтау үшін түпнұсқада AL кесіндісін жүргіземіз. Оның шеңбермен қиылысу нүктесін G арқылы белгілеп, G нүктесі арқылы NК кесіндісін жүргіземіз. ∆ANL және ∆КAN тікбұрышты үшбұрыштарын қарастырамыз. Бұл тікбұрышты үшбұрыштар ұқсас, өйткені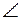 
КNА және 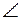ALN ішкі бұрыштары тең себебі олардың екеуі де ортақ 
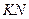доғасын керіп тұр. Осы үшбұрыштардан қарастырылған 
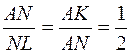қатынасын аламыз. Яғни, К нүктесі АЕ кесіндісінің ортасы екендігі дәлелденді.
 |
Осыған сәйкес А1Е1 кесіндісі қақ бөлініп, К1 нүктесі салынады. A1L1 және N1K1 кесінділерінің қиылысу нүктесі ізделінді G1 нүктесін береді. Осыған ұқсас басқа да үш нүктенің кескіндері салынады (75,ә-сурет). Алынған 8 нүктені жатық қисықпен қоса отырып берілген шеңбердің кескінін аламыз. Жоғарыда айтылып өткендей, алынған қисық эллипс болып табылады.
Берілген теориялық материалдар мен мысалдарға талдаулар жасай отырып, мынадай қорытындылар жасауға болады.
1. Егер жазық фигура құрамында үшбұрыш бар болса, онда оны бейнелеу жазықтығына кез келген үшбұрыш ретінде кескіндейміз. Бірақ фигураның одан басқа элементтерін еркін кескіндеуге болмайды.
2. Егер берілген жазық фигура құрамында квадрат бар болса, онда бейнелеу жазықтығына квадратты еркін түрде кез келген параллелограмм етіп кескіндеуге болады. Бірақ осыдан кейінгі барлық кескіндеу жұмыстарын еркін түрде орындауға болмайды. Себебі квадратты параллелограмм етіп кескіндей отырып, бейнелеу жазықтығындағы әрбір нүкте бір мәнді анықталады.
Егер жазық фигура құрамында шеңбер болса, онда бейнелеу жазықтығына шеңберді эллипс етіп кескіндей отырып, бейнелеу жазықтығындағы әрбір нүктені бір мәнді анықтаймыз. Яғни, жазық фигураның басқа элементтерін одан әрі еркін түрде кескіндеуге болмайды.
