Түзу мен жазықтықтың өзара орналасу жағдайларына берiлген есептердi шығару барысында мынадай тәсiлдi қолдануға болады. Берiлген жазықтықты қиятын бiр немесе бiрнеше көмекшi жазықтықтар жүргiзiлiп, олардың қиылысу сызықтары алынады. Осы сызықтарды пайдалана отырып берiлген есеп талаптары дәлелденедi. Бұл тәсiлдi қарсы жору әдiсiмен бiрге қолданған тиiмдi.
4-есеп. Егер жазықтық параллель түзулердiң бiреуiн қиятын болса, онда ол екiншiсiн де қиятынын дәлелдеңдер.
Есеп шарты бойынша a жазықтығы берiлген а түзуiн А нүктесiнде қияды. a жазықтығының а түзуiне параллель болатын b түзуiн де қиятынын дәлелдеу керек.
Қарсы жорып, a жазықтығы b түзуiн қимайды деп ұйғарайық. Ендi, талдаулар жасай отырып есеп шартымен немесе белгiлi аксиомаға, не теоремаға қарама-қайшы тұжырым алуымыз керек. Ол үшiн b түзуi және А нүктесi арқылы көмекшi b жазықтығын жүргiземiз. Олай болса, b жазықтығы a жазықтығын А нүктесi арқылы өтетiн с түзуi бойымен қияды. Бұдан b түзуi мен a жазықтықтары қиылыспағандықтан олар параллель. Демек, с║b болады. Бұдан b түзуiнен тысқары жатқан А нүктесi арқылы b түзуiне параллель екi а және с түзулерi жүргiзiледi. Ал бұл планиметрия аксиомасына қайшы. Олай болса, берiлген теорема дәлелдендi.
Бұл есептi қарсы жору тәсiлiн пайдаланбай да дәлелдеуге болады. Ол үшiн а║b түзулерi арқылы g жазықтығын жүргiземiз. g және a жазықтықтары m түзуi бойымен қиылысатын болсын. Сонда m түзуiнiң b түзуiн В нүктесiнде қиятынын және осы В нүктесi a жазықтығы мен b түзуiнiң де ортақ нүктесi болатынын көрсетуге болады.
Бұл тәсiлдi теоремаларды дәлелдеуде жиi қолдануға болады. Мысалы:
1. Берiлген екi түзудiң әрқайсысы үшiншi бiр түзуге параллель болса, онда олар өзара параллель.
2. Егер түзу параллель екi жазықтықтың бiрiн қиятын болса, онда ол екiншi жазықтықты да қияды.
3. Егер түзу параллель екi жазықтықтың бiрiне параллель болса, екiншiсiне де параллель.
4. Егер екi жазықтық берiлген түзуге перпендикуляр болса, онда олар өзара параллель.
5. Егер екi түзудiң әрқайсысы берiлген жазықтыққа перпендикуляр болса, онда олар өзара параллель.
Түзу мен жазықтықтың өзара орналасуына байланысты дәлелдеуге берiлген осындай есептердi көмекшi жазықтықтар жүргiзiп, олардың берiлген жазықтықтармен қиылысу сызықтарын пайдалана отырып қарсы жору арқылы шығарылады. Ал оның шығару жоспары мына түрде жалпыланады:
1) Дәлелдеу керек тұжырымды қарсы жору.
2) Берiлген жазықтықты қиятындай бiр немесе бiрнеше көмекшi жазықтықтар жүргiзу.
3) Көмекшi жазықтықтың берiлген жазықтықтарды қиятындығын дәлелдеу және олардың қиылысу сызықтарын қарастыру.
4) Құрамына көмекшi жазықтықтар мен берiлген жазықтықтардың қиылысу сызықтары енетiн қарапайым есептер (есепшелер) тiзбегiн құру. Және осы қарапайым есептердi шығару барысында берiлген есеп шартымен, не белгiлi теоремамен, не аксиомамен қайшылыққа келу.
5) Жасалған ұйғарымның дұрыс емес, ал есеп шартындағы тұжырым дұрыс деген қорытындыға келу.
Стереометрияның алғашқы тарауларын оқыту барысында басқа типтi есептердi де шығарудың жоспарын осы сияқты жалпыланады. Өйткенi түзу мен жазықтықтың әртүрлi орналасуына берiлген есептер әртүрлi жолмен шығарылатыны белгiлi, тiптi бiр есептiң өзi әртүрлi тәсiлмен шығарылуы мүмкiн. Сондықтан оқушыларға берiлген есептi шығару тәсiлдерiнiң бiрiн таңдауға көмек беретiн төмендегiдей нұсқаулар ұсынылады.
1) Есептiң шартына талдау жасай отырып оны бiрнеше қарапайым есептер тiзбегiне келтiру.
2) Болмаса, геометриялық орындар әдiсiн пайдалану.
3) Егер есеп бұл тәсiлмен шықпаса, онда қарсы жору әдiсiн қолдану.
4) Есеп ондай жағдайда да шықпаса, берiлген жазықтықты қиятын бiр немесе бiрнеше көмекшi жазықтықтар жүргiзiңдер. Құрамына жазықтықтардың қиылысу сызықтары енетiн және берiлген есептiң шешiмiне алып келетiн қарапайым есептер құрастырыңдар. Оны қарсы жору арқылы немесе тiкелей шығаруға болады.
5) Есептi шығарып оның басқа да шығару тәсiлдерiн iздестiрiңдер.
Ендi стереометрия курсының алғашқы тарауларындағы салу есептерiн шығаруда тиiмдi болып есептелетiн кейбiр дербес тәсiлдерге тоқталайық.
Салу есептерiн шығару барысында оның шартын қарапайым түрге келтiру әдiсi жиi қолданылады. Яғни, есеп шартындағы талаптардың бiраз бөлiгi уақытша ескерiлмей қарапайым есептер тiзбегiне келтiрiледi. Мысалы келтiрейiк.
5-есеп. А нүктесi арқылы өтiп, берiлген айқас а және b түзулерiнiң әрқайсысын қиятын түзу салу.
Яғни, А нүктесi арқылы өтiп, айқас а және b түзулерiн қиятын х түзуiн салу үшiн есеп шартын екi бөлiкке бөлемiз.
1) А нүктесi арқылы өтiп а түзуiн қиятын (есеп шартындағы b түзуiн қиюы керек деген талапты уақытша алып тастаймыз) х түзуiн салу. Бұндай х түзулердi шексiз түрде жүргiзуге болады және олардың барлығы А нүктесi мен а түзуi арқылы анықталатын a жазықтығында жатуы керек.
2) Осыған ұқсас, А нүктесi арқылы өтiп b түзуiн қиятын х түзуiн саламыз. Олай болса, бұндай х түзуiлерi А нүктесi және b түзуi арқылы өтетiн b жазықтығында жатуы керек. Демек, есеп шартын қанағаттандыратындай х түзуi бар болатындығын көремiз және ол iзделiндi х түзуi a және b жазықтықтарының қиылысу сызығы арқылы анықталады.
Осы тәсiлдi кеңiстiктегi нүктелердiң геометриялық орындарына қатысты салу есептерiн шығарғанда пайдаланған тиiмдi. Салу есепетерiн шығару барысында нүктелердiң геометриялық орындары, яғни геометриялық орындар әдiсi жиi пайдаланылады. Мысалы келтiрейiк.
6-есеп. Берiлген нүктеден жазықтыққа жүргiзiлген бiрдей ұзындықтағы көлбеулер табандарының геометриялық орнын табыңдар.
Шешуi. Есеп шарты бойынша берiлген S нүктесi a жазықтығынан а қашықтықта орналасса, осы нүктеден a жазықтығына түсiрiлген b> а көлбеулерi табанының геометриялық орнын салу керек. Бұл есептi шығаруды геометриялық орындар әдiсiн пайдаланып, осы жұмыстың I-тарауының 3-параграфында көрсетiлген жоспар бойынша жүргiземiз. Кеңiстiктегi S нүктесiнен бiрдей b қашықтықта жатқан нүктелердiң геометриялық орны сфера болады. Ал берiлген a жазықтығы S нүктесiнен а <b қашықтықта жатқандықтан, алынған сфера мен a жазықтығы қиылысады. Ал олардың қиылысу сызығы шеңбер болатындығын ескерсек, осы шеңбер iзделiндi нүктелердiң геометриялық орны болып табылады. Олай болса, есеп шешiмi центрi S нүктесiнен a жазықтығына түсiрiлген перпендикулярдың табаны О нүктесi болатын және радиусы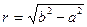 
тең шеңбер.
Ендi, дәлелдеуге берiлген стереометриялық салу есептерiн шығару барысында жиi қолдануға болатын мынадай тәсiлге тоқталайық. Есеп шартында берiлген белгiлi бiр шарттарды қанағаттандыратын (берiлген кесiндiнiң ортасы арқылы өтетiн, берiлген түзуге перпендикуляр және берiлген нүкте арқылы өтетiн және т.б.) түзу берiлген болсын. Оның қандайда бiр қасиеттерге ие болатынын (берiлген түзуге параллель, берiлген жазықтыққа перпендикуляр және т.б.) дәлелдеу керек. Есептi шығару үшiн көрсетiлген шарттарды толық немесе қандай да бiр бөлiгiн қанағаттандыратын көмекшi бiр түзу жүргiзiлiп, осы түзудiң берiлген түзумен бiр түзу екендiгi дәлелденедi. Осы тәсiлдi пайдалана отырып мына есептi шығарайық.
7-есеп. a және b жазықтықтары параллель. a жазықтығында жатқан А нүктесi арқылы b жазықтығына параллель а түзуi жүргiзiлген. Осы а түзуiнiң a жазықтығында жататынын дәлелде.
 |
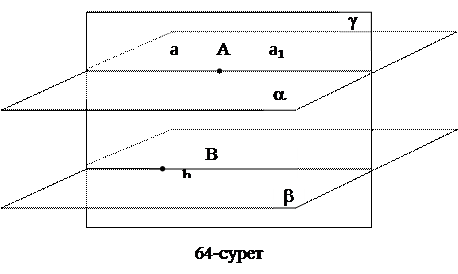Шешуi. а түзуi және b жазықтығына тиiстi В нүктесi арқылы g жазықтығын жүргiземiз (64-сурет). Ол жазықтық a және b жазықтықтарын сәйкес параллель а1 және b түзулерi бойымен қияды. а1 түзуiн қарастырайық. Ол А нүктесi арқылы өтедi және a жазықтығында жатады, яғни дәлелдеу қажеттi қасиетке ие. Содан кейiн, есеп а1 түзуi b жазықтығына параллель болатынын және а1 мен а түзулерi сәйкес келетiнiн дәлелдеуге келтiрiледi. Бұл есептердiң екеуi де қарапайым.
Келтiрiлген тәсiлдi мына төмендегi есептердi шығару барысында да қолдануға болады.
1. Қиылысушы екi жазықтықтың әрбiрiне параллель болатын түзу, олардың қиылысу сызығына да параллель болатынын дәлелде.
2. Егер екi түзу үшiншi бiр түзуге параллель болса, онда олар өзара параллель.
3. Берiлген түзудi қиятын барлық параллель түзулердiң бiр жазықтықта жататынын дәлелде және т.с.с.
