Генеральной совокупностью называется весь набор однородных объектов, изучаемых относительно некоторого качественного или количественного признака. Число всех изучаемых объектов N называется объёмом генеральной совокупности.
Выборка - это та часть генеральной совокупности, элементы которой подвергаются статистическому обследованию. Число nвошедших в выборку элементов называется объёмом выборки.
Одна из задач математической статистики – оценка параметров генеральной совокупности по данным выборки.
Статистические оценки бывают точечные (определяемые одним числом) и интервальные (определяемые двумя числами – концами интервала). Точечные оценки дают представление о величине соответствующего параметра, а интервальные характеризуют точность и достоверность оценки.
Для достоверности результатов точечная оценка должна быть несмещённой, состоятельной и эффективной. Этим условиям удовлетворяют следующие оценки:
для математического ожидания генеральной совокупности –
выборочное среднее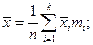 
(5)
для дисперсии генеральной совокупности –
выборочная дисперсия 
(6)
для среднего квадратичного отклонения генеральной совокупности –
стандартное отклонение 
(7)
При выборке малого объёма точечная оценка может сильно отличаться от оцениваемого параметра. Поэтому при небольшом объёме выборки (чаще всего встречающемся на практике) пользуются интервальными оценками.
Интервальная оценка- это оценка, которая определяется двумя числами- концами интервала или доверительными границами.
Если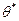 
- статическая оценка параметра 
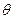, то говорят, что оценка вычислена с точностью 
, если 
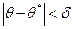(8),
то есть величина параметра 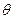попадает в интервал 
.
Статистические методы позволяют говорить о вероятности выполнения неравенства (8), поэтому надёжностью (доверительной вероятностью)оценки называется вероятность 
, с которой осуществляется это неравенство.
Интервал , который покрывает неизвестный параметр с заданной надёжностью , называется доверительным интервалом.
Доверительную вероятность (надёжность) выбирают обычно (в зависимости от важности оцениваемого признака) из значений 0.95; 0.99; 0.999.
Чтобы оценить среднее значение некоторого количественного признака 
генеральной совокупности, строят доверительный интервал для математического ожидания с доверительной вероятностью (надёжностью) .
Если признак распределен нормально и среднее квадратичное отклонение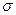 
известно, то по выборке объёма 
вычисляют среднее выборочное значение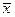 
, а так же определяют такое значение аргумента 
, что функция Лапласа 
. Тогда доверительный интервал для математического ожидания имеет вид:
(9)
Если признак распределен нормально и среднее квадратичное отклонение 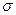неизвестно, то для построения доверительного интервала по выборке объёма nвычисляют точечные оценки: 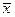– выборочное среднее; s –выборочное среднее квадратичное отклонение (
).Затем по справочной таблице значений величины 
, связанной с распределением Стьюдента, находят 
.В этом случае доверительный интервал для математического ожидания имеет вид:
(10)
Замечание. Для выборок большого объёма можно вместо формулы (10) использовать формулу (9).
