Элементы аналитической геометрии в пространстве
Плоскость
1) Уравнение плоскости, проходящей через данную точку 
перпендикулярно заданному вектору 
:
(1)
2) Общее уравнение плоскости: 
(2)
Вектор 
называется нормальным вектором плоскости (1) или (2).
3) Уравнение плоскости в отрезках на осях: 
(3)
Плоскость (3) проходит через три точки 
, 
, 
.
Угол, образованный двумя плоскостями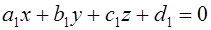 
и 
, находится по формуле
, где 
и 
.
Условие параллельности двух плоскостей
Условием параллельности плоскостей, заданных общими уравнениями, является пропорциональность коэффициентов при переменных, т.е. 
Условие перпендикулярности двух плоскостей
Условием перпендикулярности плоскостей, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных, т.е.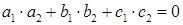 
.
Расстояние от точки до плоскости
Пусть даны точка 
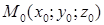и плоскость 
Общее уравнение плоскости
Всякое уравнение первой степени с тремя переменными есть уравнение плоскости
(2)
Частные случаи:
1) Если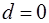 
, то уравнение (2) примет вид 
Это уравнение определяет плоскость, проходящую через начало координат.
2) Если 
, то уравнение 
определяет плоскость, параллельную оси 
.
3) Если 
, то уравнение 
определяет плоскость, проходящую через ось .
4) Если 
, то уравнение 
определяет плоскость, параллельную плоскости 
.
5) Если 
, то уравнение 
(или 
) определяет координатную плоскость .
6) Если 
, то уравнение 
определяет плоскость, параллельную оси 
.
7) Если 
, то уравнение 
определяет плоскость, проходящую через ось .
8) Если 
, то уравнение 
определяет плоскость, параллельную плоскости 
.
9) Если 
, то уравнение 
(или 
) определяет координатную плоскость .
10) Если 
, то уравнение 
определяет плоскость, параллельную оси 
.
11) Если 
, то уравнение 
определяет плоскость, проходящую через ось .
12) Если 
, то уравнение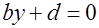 
определяет плоскость, параллельную плоскости 
.
13) Если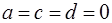 
, то уравнение 
(или 
) определяет координатную плоскость .
Прямая в пространстве
1) Прямая в пространстве может быть задана двумя пересекающимися плоскостями, уравнения которых 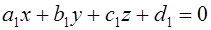и . Тогда уравнения прямой будут
(4)
Уравнения (4) называются общими уравнениями прямой (в пространстве).
2) Уравнения прямой, проходящей через точку и параллельной вектору 
, получаются на основе условия коллинеарности двух векторов 
и 
:
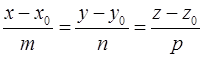(5)
Уравнения (5) называются каноническими уравнениями прямой.
Вектор называется направляющим вектором прямой (5).
3) Уравнения прямой, проходящей через две заданные точк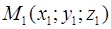и 
и 
имеют вид:
4) Если каждое из отношений (5) приравнять к параметру 
, то получим уравнения
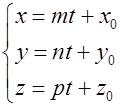(6)
Уравнения (6) называются параметрическими уравнениями прямой.
Угол между двумя прямыми с направляющими векторами 
и 
находится по формуле
.
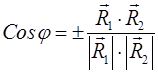Условие параллельности двух прямых
Условием параллельности прямых является пропорциональность координат направляющих векторов (т.к. они коллинеарны), т.е. 
