Элементы аналитической геометрии на плоскости
1) Расстояние между точками 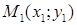 и
и 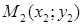 :
:

2) Координаты точки  , делящей отрезок с концами
, делящей отрезок с концами 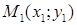 и
и 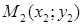 в отношении
в отношении  :
: 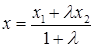 ,
, 
Прямая линия на плоскости
1) Уравнение прямой с угловым коэффициентом
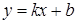 , где
, где  – угловой коэффициент (тангенс угла
– угловой коэффициент (тангенс угла 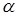 ),
),  – величина отрезка, отсекаемого прямой на оси
– величина отрезка, отсекаемого прямой на оси 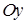 .
.
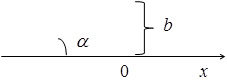 |
2) Уравнение прямой, проходящей через заданную точку в данном направлении
Дано: точка 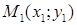 и угловой коэффициент
и угловой коэффициент  (задает направление)
(задает направление)
Уравнение прямой: 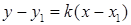 (1)
(1)
При разных значениях  уравнение (1) является уравнением различных прямых, проходящих через точку
уравнение (1) является уравнением различных прямых, проходящих через точку 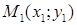 . Уравнение (1) называют уравнением пучка прямых, проходящих через данную точку. Уравнением (1) не определяется только прямая, параллельная оси
. Уравнение (1) называют уравнением пучка прямых, проходящих через данную точку. Уравнением (1) не определяется только прямая, параллельная оси 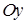 (она не имеет углового коэффициента).
(она не имеет углового коэффициента).
3) Уравнение прямой, проходящей через две точки 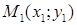 и
и 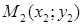 :
:
 или
или 
Угловой коэффициент этой прямой  .
.
4) Уравнение прямой в отрезках на осях:  , где
, где 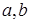 – величины отрезков, отсекаемых прямой на осях
– величины отрезков, отсекаемых прямой на осях 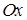 и
и 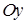 .
.
5) Уравнение прямой, проходящей через данную точку 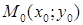 перпендикулярно заданному вектору
перпендикулярно заданному вектору  :
:
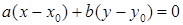
6) общее уравнение прямой: 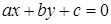 , (2) где
, (2) где 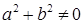
Частные случаи:
а) Пусть  , тогда уравнение (2) можно записать в виде
, тогда уравнение (2) можно записать в виде 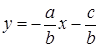 .
.
Обозначим 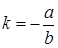 ,
, 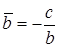 . Тогда получим
. Тогда получим 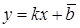 .
.
• Если  ,
,  , то получится уравнение
, то получится уравнение  (уравнение прямой, проходящей через начало координат).
(уравнение прямой, проходящей через начало координат).
• Если 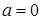 ,
,  , то получится уравнение
, то получится уравнение 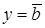 (уравнение прямой, параллельной оси
(уравнение прямой, параллельной оси 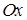 ).
).
• Если 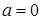 ,
,  , то получится уравнение
, то получится уравнение 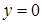 (уравнение оси
(уравнение оси 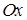 ).
).
б) Пусть 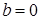 ,
,  , тогда уравнение (2) примет вид
, тогда уравнение (2) примет вид 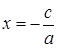 . Обозначим
. Обозначим 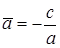 . Тогда получим:
. Тогда получим:
• 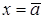 , если
, если  (уравнение прямой, параллельной оси
(уравнение прямой, параллельной оси 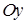 );
);
• 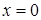 , если
, если  (уравнение оси
(уравнение оси 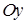 )
)
Следовательно, при любых значениях коэффициентов 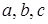 (где
(где 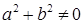 ) уравнение (2) является уравнением некоторой прямой линии на плоскости
) уравнение (2) является уравнением некоторой прямой линии на плоскости  .
.
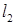 Угол между двумя прямыми.
Угол между двумя прямыми.
 |
Пусть заданы две прямые:  и
и  . Угол
. Угол 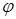 получается поворотом прямой
получается поворотом прямой 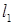 к прямой
к прямой 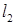 против часовой стрелки.
против часовой стрелки.
Из рисунка видно, что 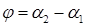 . Так как
. Так как 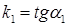 ,
,  (предполагается, что
(предполагается, что 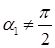 и
и  ), то получаем
), то получаем 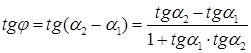
Таким образом, получаем следующую формулу для нахождения угла между прямыми:
 .
.
Кроме того, для вычисления углов 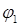 и
и 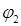 между прямыми, заданными общими уравнениями
между прямыми, заданными общими уравнениями  и
и 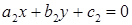 , справедлива формула
, справедлива формула
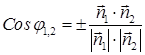 , где
, где 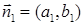 и
и 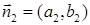 .
.
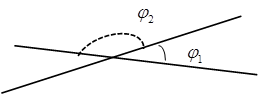 |
Условие параллельности двух прямых
Равенство угловых коэффициентов является необходимым и достаточным условием параллельности двух прямых, т.е.  .
.
Условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при переменных х и у, т.е. 
Условие перпендикулярности двух прямых
Для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку, т.е. 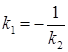 (или
(или 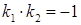 ).
).
Условием перпендикулярности прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у, т.е.  .
.
Точка пересечения прямых
Пусть даны прямые  и
и 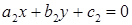 .
.
Координаты точки пересечения этих прямых должны удовлетворять уравнению каждой прямой. Поэтому, они могут быть найдены из системы уравнений
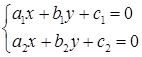
Если прямые не параллельны и не совпадают (т.е. 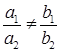 ), то решение данной системы дает координаты единственной точки пересечения этих прямых.
), то решение данной системы дает координаты единственной точки пересечения этих прямых.






