Требуется построить линию пересечения заданных плоскостей.
Решение задачи заключается в нахождении двух точек общих для данных плоскостей, через которые можно провести прямую линию. Плоскость, заданная треугольником АВС можно представить, как прямые линии (АВ), (АС), (ВС). Точка пересечения прямой (АВ) с плоскостью a - точка D, прямой (AС) -F. Отрезок [DF] определяет линию пересечения плоскостей. Так как - горизонтально проецирующая плоскость, то проекция D1F1 совпадает со следом плоскости П1 таким образом остается только построить недостающие проекции DF на П2 и П3.

| 
| 
| 
|
| |||

| |||

| |||
| а) модель | б) эпюр | ||
| Рисунок 64. Пересечение плоскости общего положения с горизонтально проецирующей плоскостью |
Рассмотрим общий случай пересечения плоскостей, когда плоскости занимают общее положение в пространстве.
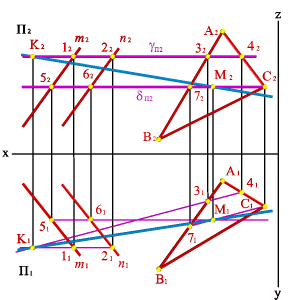
Задача. Дано: Две плоскости общего положения a()n,m и b (ABC) (рис.65).
Требуется построить линию пересечения плоскостей a и b.

| 
| 
| 
|
| |||

| |||

| |||
| а) модель | б) эпюр | ||
| Рисунок 65. Пересечение плоскостей общего положения |
Рассмотрим последовательность построения линии пересечения плоскостей a(m//n) и b(АВС). По аналогии с предыдущей задачей для нахождения линии пересечения данных плоскостей проведем вспомогательные секущие плоскости g и d. Найдем линии пересечения этих плоскостей с заданными плоскостями. Плоскость g пересекает плоскость a по прямой (12), а плоскость b - по прямой (34). Точкапересечения этих прямых- К,которая одновременно принадлежит трем плоскостям a, b и g,т.е. искомой линии пересечения плоскостей a и b. Плоскость d пересекает плоскости a и b по прямым (56) и (7C), точка их пересечения М расположена одновременно в трех плоскостях a, b, d и принадлежит прямой линии пересечения плоскостей a и b. Таким образом, прямая (КМ) является линией пересечения плоскостей a и b.
Некоторого упрощения при построении линии пересечения плоскостей можно достичь, если вспомогательные секущие плоскости проводить через прямые, задающие плоскость. В этом случае точки, определяющие положение линии пересечения плоскостей, находятся как точки пересечения прямой и плоскости.
| взаимно перпендикулярные плоскости | 
|
Частный случаем пересечения плоскостей являются взаимно перпендикулярные плоскости.
Из стереометрии известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей, перпендикулярных данной плоскости a(h,f). Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a. Для того, чтобы через точку А провести плоскость, перпендикулярную плоскости a(h, f),необходимо из точки А провести прямую n, перпендикулярную плоскости a(h, f), (горизонтальная проекция n1 перпендикулярна горизонтальной проекции горизонтали h1, фронтальная проекция n2 перпендикулярна фронтальной проекции фронтали f2). Любая плоскость, проходящая через прямую n будет перпендикулярна плоскости a(h, f), поэтому для задания плоскости через точку А проводим произвольную прямую m. Плоскость заданная двумя пересекающимися прямыми (m,n),будет перпендикулярна плоскости a(h, f) (рис.66).

| 
| 
| 
|
| |||

| |||
| а) модель | б) эпюр | ||
| Рисунок 66. Взаимно перпендикулярные плоскости |






