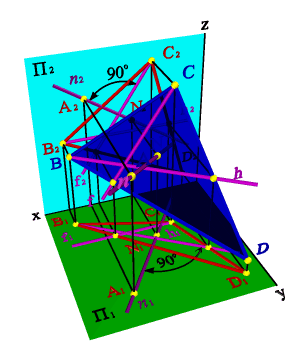
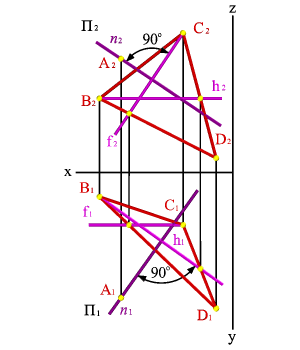
Требуетсяпостроить прямую линию n проходящую через точку А и перпендикулярную плоскости ВСD.
В плоскости ВСD построим фронталь f и горизонталь h. В горизонтальной плоскости проекций проведем через точку А1 прямую n1 перпендикулярно горизонтальной проекции горизонтали h1, а на фронтальной плоскости проекций через точку А2 прямую n2 перпендикулярно фронтальной проекции фронтали f2, согласно, теореме о перпендикуляре к плоскости, полученная прямая n будет перпендикулярна плоскости ВСD.

| 
| 
| 
|
| |||

| |||

| |||
| а) модель | б) эпюр | ||
| Рисунок 61. Прямая, перпендикулярная плоскости |
| Взаимное расположение точки и плоскости | 
|
Возможны два варианта взаимного расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.
Если точка принадлежит плоскости, то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.
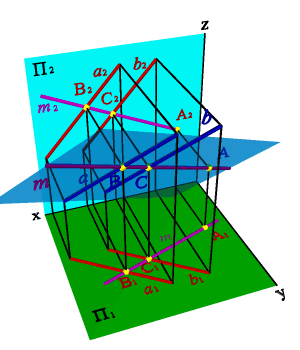
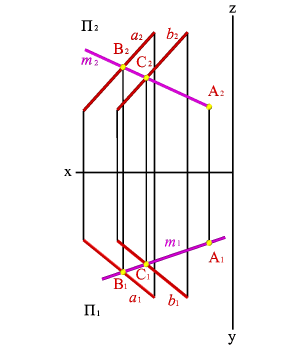
Рассмотрим пример (рис.62). Построение проекции точки А принадлежащей плоскости общего положения заданной двумя параллельными прямыми a(ab).
Задача. Дано: плоскость (а, b)и фронтальная проекция точки А.
Требуетсяпостроить горизонтальную проекцию точки А, если известно, что она лежит в плоскости (а, b).

| 
| 
| 
|
| |||

| |||

| |||
| а) модель | б) эпюр | ||
| Рисунок 62. Точка, принадлежащая плоскости |
Через точку А 2 проведем проекцию прямой m2, пересекающую проекции прямых a 2 и b 2 в точках С2 и В2 (С Îa, B ÎaÞ mÎa). Построив проекции точек С 1 и В 1, определяющие положение m1, находим горизонтальную проекцию точки А (А 1Î m1, m ÎaÞ А Îa).
| Взаимное расположение плоскостей | 
|
Две плоскости в пространстве могут быть либо параллельны, в частном случае совпадать друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют собой частный случай пересекающихся плоскостей
| Параллельные плоскости | 
|
Плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Это определение хорошо иллюстрируется задачей, через точку В провести плоскость параллельную плоскости, заданной двумя пересекающимися прямыми (a, b) (рис.63).
Задача. Дано: плоскость общего положения, заданную двумя пересекающимися прямыми (a, b) и точка В.
Требуется через точку В провести плоскость, параллельную плоскости (a, b) и задать её двумя пересекающимися прямыми c и d.
Согласно определения, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны между собой.
Для того, чтобы провести на эпюре параллельные прямые необходимо воспользоваться свойством параллельного проецирования - проекции параллельных прямых - параллельны между собой.






