Теорема 3.1.3 Имеет место равенство 
, т.е. производная по направлению 
равна скалярному произведению векторов градиента и орта направления .
Следствие. Вектор в каждой точке направлен по нормали к линии уровня, проходящей через данную точку возрастания функции. При этом
 .
| (15) |
Теорема 3.1.4. Скорость изменения функции 
по некоторому направлению равна проекции вектора градиента на это направление, т.е. 
.
Пример 3.1.1. Найти производную функции 
в точке 
в направлении, составляющем с осью 
угол 
. Определить направление максимального роста функции в данной точке.
Имеем 
, 
, 
, 
. Следовательно, если через обозначим данное направление, то согласно (13), получим 
.
Рисунок 5.
| Градиент функции поля в данной точке имеет вид  . Этот вектор указывает направление, в котором функция растет быстрее, чем по другим направлениям. На рис.5. схематически изображены точка ,направление  с  и направление  .
|
Максимальное значение производной (см. формулу (15) в точке равно по модулю 
.
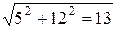Пример 3.1.2. Найти производную 
в точке 
по направлению к точке 
.
Имеем 
, 
с направляющими косинусами вектора 
: 
, 
.Тогда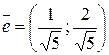 
– орт направления . Далее, имеем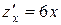 
, 
, 
, 
, а значит, 
. Отрицательность 
означает, что функция в этом направлении убывает.
Упражнения к §3.1.
1) Построить линию уровня функции 
, проходящую через точку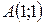 
. Построить градиент 
и убедится, что он перпендикулярен построенной линии уровня.
2) Для функции 
построить линии уровня и градиент. Сравнить их направления в точках 
и 
.
3) Найти наибольший рост (наибольшую крутизну) поверхности 
в точке 
.
4) Найти производную функции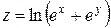 
в направлении, параллельном биссектрисе координатного угла.
§3.2 Касательная плоскость и нормаль к поверхности.
Касательная и нормаль к поверхности
Пусть 
фиксированная точка на поверхности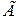 
, заданной функцией 
или уравнением 
.
Определение. Касательной плоскостью к в точке называется плоскость, в которой расположены касательные к всевозможным кривым, проведенным на через. Нормалью называется прямая, проходящая через перпендикулярно.
Из определения 
следует, что нормальный вектор касательной плоскости 
и направляющий вектор прямой 
совпадают.
Уравнения имеют вид:
a) Если 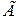задана явно функцией 
, то:
| (16) |
b) Если 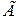задана уравнением , то:
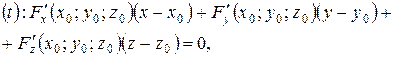
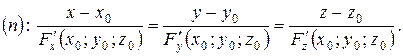
| (17) |
Пример 3.2.1. Составить уравнения касательной и нормали в точке к кривой, заданный неявно уравнением.
Положим 
. Тогда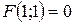 
. Далее имеем 
, 
, 
, 
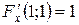. Условие 
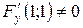обеспечивает существование однозначной неявной функции 
в окрестности точки 
. Уравнение касательной 
имеет вид 
, где 
, т.е.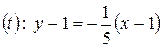 
. Уравнение нормали имеет вид 
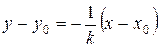, т.е. 
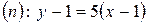(формулы (16)).
