Цель: обобщение и систематизация знаний, умений по данной теме; формирование практических навыков в решении задач; развитие интереса к изучению физики
Краткие теоретические сведения
Таблица 2.1 – Основные законы и формулы
| Физические законы, формулы, переменные | Формулы |
| Ускорение при криволинейном движении: 1) нормальное где R – радиус кривизны траектории, 2) тангенциальное,3) вектор полного ускорения,4) модуль полного ускорения. | 1)  ,2)  ,
3)  ,4) 
|
1) угловое перемещение  .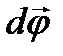
2) угловая скорость  :
где dt – интервал времени.
3) угловое ускорение  :
Единицы измерения:
 ;  ;  .
| 2)  ;
3)  .
|
Равномерное вращение:
1) период вращения Т:
2) частота вращения ν:
Единицы измерения:
 ; 
| 1)  ;
2)  .
|
| Равноускоренное вращение β=const: 1) уравнение углового перемещения где ω0 – начальная угловая скорость 2)уравнение угловой скорости: где R – радиус – расстояние от центра вращения до материальной точки; 3) нормальное ускорение: 4) тангенциальное ускорение: 5)полное ускорение: | 1)  ;
2)  ;
3)  ;
4) 
5)  .
|
| Связь линейной υ и угловой скорости ω: |  ,
|
1)Момент инерции J материальной точки относительно оси вращения:
где mi– масса точки, ri – расстояние от оси вращения до материальной точки;
2) Момент инерции системы (тела) относительно оси вращения:[1]
| 1)  ;
2)  .
|
| Теорема Штейнера: где JZ– момент инерции относительно произвольной оси Z, JC– момент инерции относительно параллельной оси, проходящей через центр масс С, а – расстояние между осями. | 
|
| 1)Кинетическая энергия вращения ЕВР: где JZ - момент инерции тела относительно произвольной оси Z; ω – угловая скорость материальных точек тела. 2)Полная кинетическая энергия тела: ЕК – кинетическая энергия поступательного движения тела, m– масса тела, υ –скорость тела. | 1)  ;
2)  .
|
1) Момент силы  :
где  – радиус – вектор, проведенный в точку приложения силы  ;
2) Модуль момента силы:
где α – угол между векторами и , l – плечо силы.
| 1)  ;
2)  .
|
Основное уравнение динами вращательного движения твердого тела:
где  – момент силы, J – главный момент инерции тела(момент инерции относительно главной оси),  – угловое ускорение.
| 
|
1) Импульс тела:
2) Закон сохранения импульса
| 1)  ;
2) 
|
1)Момент импульса материальной точки  :
где – радиус – вектор,  - импульс точки, m – масса,  –скорость точки,
2) Момент импульса твердого телаотносительно оси Z:
где mi – масса отдельной части твердого тела, υi –скорость частицы,  – радиус – вектор, ω – угловая скорость, JZ - момент инерции тела относительно произвольной оси Z,
3) Закон сохранения момента импульса:
| 1)  ,
2)  ,
3) 
|
Работа силы F:
где Fs – проекция силы на ось, направленную вдоль движения, S – модуль перемещения, α - угол между вектором силы и направлением перемещения
| 
|
Мощность N:
dA – элементарная работа, dt – интервал времени,  – вектор силы,  - перемещение,  - скорость тела.
| 
|
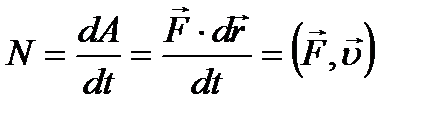
Кинетическая энергия К:
m – масса тела; υ – скорость. 
| 
|
Потенциальная энергия П:
3) тела, поднятого над землей на высоту h;
4) упруго деформированной пружины, жесткостью k.
| 1)  ;
2) 
|
| Закон сохранения энергии: | 
|
| КПД (коэффициент полезного действия): где Апол - полезная работа, Азат - затраченная работа. | 
|
Примеры решения задач
1. Материальная точка движется по окружности радиусом 1 м согласно уравнению 
. Найти скорость, тангенциальное, нормальное и полное ускорение в момент времени t = 2с.
Дано:
,
R = 1м,
t = 2с.
Найти:
υ –?
аτ –?
аn –?
а –?
Решение
Рисунок 2.2
Скорость движения материальной точки равна первой производной от перемещения во времени тогда,
,
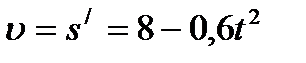Тангенциальное ускорение найдем, взяв первую производную от скорости во времени,
,
Нормальное ускорение определяется по формуле
,
Вектор полного ускорения 
равен геометрической сумме векторов 
и 
. Модуль ускорения же,
;
;
Ответ: 
, 
, 
, 
2.Точка начинает двигаться по окружности радиуса R=16 м с тангенциальным ускорением aτ=10 м/с2. 1)Чему равно полное ускорение точки через три секунды t=3с после начала движения? Решение поясните рисунком.2)Чему равна величина угловой скорости и углового ускорения при этом движении в этот момент времени?
Дано:
R = 16 м
t= 3 с
aτ = 10 м/с2
Найти:
а =?
ω=?
ε=?
Решение:
Рисунок 2.6
1) Полное ускорение а можно определить по тереме Пифагора.
Нормальное ускорение
где υ – скорость через t= 3 с. Из формулы равноускоренного движения
,
где υ – скорость точки, υ0 – начальная скорость точки, тогда
2)Угловая скорость ω равна
.
Угловое ускорение β
.
Ответ: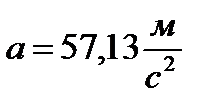 
, 
, 
3.Колесо, вращаясь равноускорено, достигло угловой скорости ω=20 рад/с и через N=10 оборотов после начала вращения. Найти угловое ускорение β колеса.
Дано:
ω=20 рад/с,
N=10
Найти:
β –?
Решение
Запишем уравнения движения для равноускоренного вращательного движения:
,
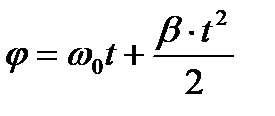где φ – угловое перемещение, ω0 – начальная угловая скорость, β – угловое ускорение;
,
где ω – угловая скорость.
Так как по условию задачи ω0 = 0, тогда уравнения движения примут вид:
, (1)
, (2)
Выразим из уравнения (1) угловое ускорение ε
. (3)
С другой стороны 
, где N – число оборотов колеса, тогда уравнение (3) можно записать в виде:
. (4)
Из уравнения (2) выразим время t
,
подставим в (4)
,
отсюда
,
,
.
Ответ: 
4.Найти радиус R вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2,5 раза больше скорости v2 точки, лежащей на расстоянии r=5 см ближе к оси колеса.
Дано:
,
r=5 см = 5·10-2м.
Найти:
R–?
Решение
Рисунок 2.7
Поскольку угловые скорости всех точек колеса одинаковы, то величины линейных скоростей будут определяется выражениями:
, 
,
где R – радиус колеса, тогда отношение линейных скоростей
.
Преобразуем выражение:
,
,
,
отсюда
.
Ответ: 
.
5. Колесо, вращаясь равнозамедленно, уменьшило за время 1 мин частоту вращения от 300 об/ мин до 180 об/мин. Найти число оборотов, сделанных колесом за это время.
Дано:
t = 1 мин =60 с,
ν1 = 300 об/ мин = 5 об/с,
ν2 = 180 об/мин = 3 об/с.
Найти:
N–?
Решение
Число оборотов N, сделанных колесом за время t:
,
где φ – угол поворота за время t, равный при равнозамедленном движении
,
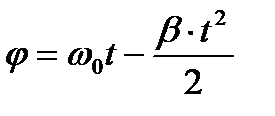ω0 – начальная угловая скорость, β – угловое ускорение.
,
,
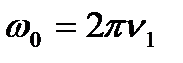тогда
,
.
Ответ: 
6.Тонкий стержень длиной k=40 см и массой m= 0,6 кг вращается вокруг своей оси, проходящей через середину стержня, перпендикулярно его длине. Уравнение вращения стержня 
, где А=1 рад/с; В=0,1 рад/с3. Определите вращающий момент М в момент времени t = 2 с.
Дано:
k=40 см = 0,4 м,
m= 0,6 кг,
,
А=1 рад/с,
В=0,1 рад/с3,
t = 2 с.
Найти:
М –?
Решение
Согласно уравнению динамики вращательного движения твердого тела:
, (1)
где М – вращающий момент, β – угловое ускорение, J – момент инерции стержня.
Момент инерции прямого тонкого стержня длиной k, вращающегося вокруг своей оси, проходящей через середину стержня
. (2)
По определению угловая скорость
.
Угловое ускорение
.
В момент времени t = 2 с, 
, тогда с учетом (2)
,
,
.
Ответ: 
.
7.Чему равен момент инерции J тонкого прямого стержня длиной L=0,5 м и массой m=0,2 кг относительно оси, перпендикулярной к его длине и проходящей через точку стержня, которая удалена на l=0,15 м от одного из его концов.
Дано:
L=0,5 м
m=0,2 кг
l =0,15 м
Найти:
J-?
Решение:
Рисунок 2.8
Момент инерции стержня находим по теореме Штейнера.
,
где J – моментинерции тела относительно произвольной оси, JC – моментинерции относительно параллельной оси проходящей через его центр масс, m – масса стержня, а – расстояниемежду осями.
Момент инерции стержня
,
где L – длина стержня.
Тогда,
.
Ответ: J = 6·10-3кг·м2.
8.Шар скатывается по наклонной плоскости с углом наклона α=300. Какую скорость v будет иметь центра шара относительно наклонной плоскости через t=1,5 с. Если его начальная скорость была равно нулю?
Дано:
α=300,
t=1,5 с,
υ0 = 0 м/с.
Найти:
υ–?
Решение:
По закону сохранения энергии
где 
− момент инерции шара, 
− связь линейной и угловой скорости,h=lsinα, 
− так как движение происходит под действием постоянной силы, то движение равноускоренное.
После подстановки
Учтем, что 
, после замены, имеем
Ответ: 
9.Маховик вращается по закону φ = 10 t + t3 (рад). Момент инерции маховика 5 кг·м2. Определить момент силы, действующий на маховик, в момент времени 1с.
Дано:
φ = 10 t + t3рад,
J=5 кг·м2,
t=1c,
Найти:
М=?
Решение:
Из основного уравнения динамики для вращательного движения
,
где момент инерции J, β – угловое ускорение.
,
Тогда момент силы
Н
Ответ: М=30 Н·м.
10.Однородный стержень длиной l=1 м и массой m=0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением ε вращается стержень, если на него действует момент сил М=98,1мН·м?
Дано:
l =1 м,
m=0,5 кг,
М=98,1мН·м = 98,1·10-3Н·м.
Найти:
β–?
Решение
Из основного уравнения динамики вращательного движения момент сил равен:
где J – момент инерции стержня, относительно оси, проходящей через его середину,
,
тогда
,
,
.
Ответ: 
10.Колесо радиуса 0,2 м с равномерно распределенной по ободу массой 5 кг вращается относительно неподвижной оси, перпендикулярной его плоскости и проходящей через его центр, так, что зависимость угла поворота колеса от времени задается уравнением j = 5+4t2–t3 (рад). Определить для момента времени t = 1 с момент импульса L колеса; момент M действующей силы; кинетическую энергию T колеса.
Дано:
R = 0,2 м,
m = 5 кг,
j = 5+4t2–t3 (рад),
t = 1 с.
Найти:
L –?
M –?
T –?
Решение
Угловая скорость w вращения равна первой производной от угла поворота по времени:
(рад/с),
для момента времени t = 1 с
.
Угловое ускорение e вращения равно первой производной от угловой скорости по времени:
,
для момента времени t = 1 с
При вращении абсолютно твердого тела вокруг неподвижной оси каждая точка тела движется по окружности постоянного радиуса Ri, со скоростью υi, перпендикулярной радиусу. Момент импульса отдельной частицы равен
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:
,
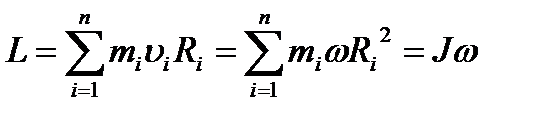где J – момент инерции тела относительно главной оси,
, тогда
,
,
.
На основании основного уравнения динамики вращательного движения
,
,
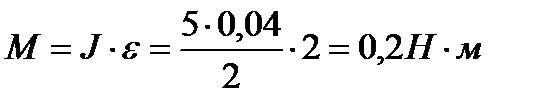
Кинетическая энергия колеса (диска)
,
,
.
Ответ: 
, 
, 
.
11.Горизонтальная платформа массой m = 80 кг и радиусом R= 1м вращается с угловой частотой ν1= 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой ν2 будет вращаться платформа, если человек опустит руки, уменьшит свой момент от J1=2,94 до J2=0,98 кг·м2? Считать платформу однородным диском.
Дано:
m = 80 кг,
R= 1м,
ν1= 20 об/мин = 1/3 об/с,
J1=2,94 кг·м2,
J2=0,98 кг·м2.
Найти:
ν2 –?
Решение
Момент импульса платформы и человека с расставленными руками
,
Момент инерции платформы
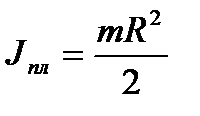
Угловая скорость
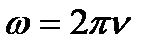
Момент импульса платформы и человека с опущенными руками
Закон сохранения момента импульса
,
тогда
Частота вращения
Ответ: 
12. Молот массой m1 =200 кг падает на поковку, масса m2 которой вместе с наковальней равна 2500 кг. Скорость u1 молота в момент удара равна 2 м/с. Найти: кинетическую энергию молота в момент удара; энергию, переданную фундаменту; энергию, затраченную на деформацию поковки; КПД удара молота о поковку. Удар считать абсолютно неупругим.
Дано:
m1 =200 кг,
m2 = 2500 кг,
u1 = 2 м/с.
Найти:
Т1 –?
Т –?
η –?
Решение.
Кинетическую энергию молота в момент удара найдем по формуле:
.
Запишем закон сохранения импульса при неупругом ударе:
,
где u2 – скорость поковки перед ударом, u - скорость молота и поковки после удара. Так как наковальня с поковкой покоились, то u2=0. Следовательно,
.
Энергия, переданная фундаменту, равна кинетической энергии системы после удара:
.
На деформацию поковки идет разность кинетических энергий:
Т = Т1 - Т2 = 370 Дж.
КПД удара равно отношению энергии, потраченной на деформацию поковки, к первоначальной энергии, т.е.
.
Ответ: 400 Дж; 29,6 Дж; 370 Дж; 92,6%.
