Общая схема головной подпрограммы сеточного алгоритма приведена на рис. 3. На шаге 1 выполняется подпрограмма 
, выполняющая инициализацию переменных. Затем в цикле 
с меткой 2 выполняется корректировка сеточной области в соответствии с описанием идеи алгоритма из раздела. Одна итерация соответствует одной корректировке. Головная подпрограмма сеточного алгоритма оформляется в виде независимого процесса, который выполняется до тех пор, пока переменная 
не примет значение 
(истина). Начальную установку переменной в значение 
(ложь) осуществляет головной процесс, соответствующий основной программе. Он же присваивает переменной значение 
, когда вычислительный процесс нужно остановить. В качестве текущего приближения решения задачи головная программа использует текущее значение нулевой вершины центральной ячейки 
, координаты которой вычисляются по формуле.
В теле цикла 
выполняются следующие действия. На шаге 3 организуется 
параллельных потоков управления (нитей), которые независимо друг от друга вычисляют псевдопроекции из целевой точки 
на пересечение i -той ячейки с многогранником M 
. Напомним, что 
равно количеству MPI-процессов, и в соответствии с формулой равно количеству ячеек в кубической сеточной области. Схема подпрограммы вычисления псевдопроекции детально описана в разделе.
Рис. 3. Головная подпрограмма сеточного алгоритма.
В цикле 
с меткой 5 для полученных на шаге 3 точек псевдопроекций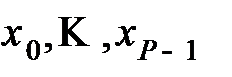 
вычисляется номер 
ячейки, на которой достигается максимум C целевой функции. Для корректной работы цикла 5 переменным и C на шаге 4 присваиваются начальные значения 
и 
соответственно. Значение соответствует минимальному машинному значению целого типа, – минимальному машинному значению вещественного типа. Подпрограмма, вычисляющая точку 
псевдопроекции точки 
на пересечение многогранника 
с ячейкой с номером , присваивает координате 
значение 
в том случае, когда точка 
псевдопроекции не принадлежит многограннику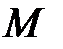 
. Эта ситуация возникает в случае, когда пересечение многогранника с ячейкой с номером является пустым. Если же принадлежит многограннику, то в силу предположения о том, что все процессы находятся в положительной области координат, значение не может быть отрицательным. Указанное условие проверяется на шаге 6. Случаи 
из рассмотрения исключаются. Если при выполнении цикла 5 оказывается, что ни одна из ячеек сеточной области не имеет непустого пересечения с многогранником 
, то в переменной сохраняется значение . Этот факт проверяется на шаге 7. В этом случае шаг сетки 
, длина 
ребра сеточной области и координаты целевой точки 
увеличиваются в 
раз, где – положительная константа, являющаяся параметром алгоритма (шаг 13 на рис. 3).
Если на шаге 7 выясняется, что 
, значит найдена ячейка с номером 
, имеющая непустое пересечение с многогранником, на которой достигается максимум целевой функции. В этом случае на шаге 8 вычисляется вектор 
, представляющий нулевую вершину новой центральной ячейки сеточной области. Схема подпрограммы вычисления нулевой вершины ячейки с порядковым номером k 𝛼 приведена на рис. 4. Вычисления осуществляются с использованием формул, и.
Рис. 4 . Схема подпрограммы zero вычисления нулевой
вершины ячейки с порядковым номером k𝛼.
На шаге 9 (рис. 3) анализируется, насколько новая центральная ячейка далеко отстоит от предыдущей. Если расстояние между новой и старой центральными ячейками превышает 
(где 
– длина ребра кубической сеточной области), то длина ребра кубической сеточной области , шаг сетки 
и координаты целевой точки 
на шаге 10 увеличиваются в 1.5 раза. Если расстояние между новой и старой центральными ячейками меньше 
, то длина ребра кубической сеточной области , шаг сетки и координаты целевой точки на шаге 11 уменьшаются в 2 раза. Величина 
, используемая в шагах 10 и 11, в общем случае является параметром алгоритма. Если же отклонение лежит в пределах от до , то корректировка значений , и не производится. Величины 
и 
также являются в общем случае параметрами алгоритма.
На шаге 12 сеточная область сдвигается по вектору 
, и в качестве текущей нулевой вершины 
центральной ячейки сеточной области берется точка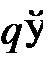 
.
2.2. Схема подпрограммы инициализации переменных init
Подпрограмма инициализации переменных выполняет ввод исходных данных и инициализацию переменных. Схема подпрограммы приведена на рис. 5. На шаге 1 вводятся значения переменных: n – размерность пространства решений; m – число неравенств в системе ограничений; R – начальное значение длины ребра сеточной области, обеспечивающее покрытие многогранника M; p – количество итераций при построении псевдопроекции, выполняемое между обновлениями входных данных (этот параметр используется в подпрограмме 
обновления исходных данных); K – количество ячеек в сеточной области по одному измерению; u – размерность подвектора; L – число независимых фейеровских итераций на подвекторах в подпрограмме вычисления псевдопроекции (см. рис. 6); T – масштабирующий коэффициент для вычисления координат целевой точки z. На шаге 2 проверяется условие (assert) 
, означающее, что размерность пространства решений 
кратно размерности подвектора 
. На шаге 3 осуществляется ввод исходных данных задачи линейного программирования: A – матрица коэффициентов неравенств; b – столбец свободных членов; c – вектор коэффициентов целевой функции. Также здесь вводится вектор G, содержащий начальные координаты нулевой вершины кубической сеточной области. Шаг 4 присваивает переменной P значение, равное количеству доступных MPI‑процессов и вычисляемое с помощью системной функции 
.
Рис. 5. Схема подпрограммы инициализации переменных init.
На шаге 5 проверяется условие (assert) 
, означающее, что общее количество ячеек сеточной области равно количеству процессов. На шаге 6 формируется инвариантная часть расширенного столбца 
свободных членов, определяемого по формуле. На шаге 7 происходит инициализация матрицы 
путем присваивания всем ее элементам нулевых значений. На шаге 8 определяются ненулевые элементы матрицы в соответствии с системой неравенств. На шагах 9 и 10 строится расширенная матрица 
, определяемая формулой. На шаге 11 в качестве начального значения длины r ребра сеточной области определяется значение R, обеспечивающее покрытие многогранника M, и вычисляется значение 
длины ребра ячейки. На шаге 12 в качестве начальной нулевой вершины g кубической сеточной области берется точка G, определяющая такое положение сеточной области, при котором она полностью покрывает многогранник M. На шаге 13 вычисляются координаты целевой точки z по формуле 
. На шаге 14 вычисляется нулевая вершина q центральной ячейки сеточной области по формуле. На последнем шаге вычисляется вектор 
начальных целочисленных координат центральной ячейки по формуле.
