Построение сеточной области

МАГИСТЕРСКАЯ ДИССЕРТАЦИЯ

По направлению подготовки 01.04.02 Прикладная математика и информатика

 

Сеточный алгоритм решения задачи линейного программирования

Выполнил студент Леготин Игорь Олегович

академическая группа МПмаг-202, курс 2 очной формы обучения

____________________________________

 

«____» ____________ 2016 г.

 

 

ДОПУЩЕН К ЗАЩИТЕ Протокол заседания кафедры от «___» ___________ 2016 г. № ____ Заведующий кафедрой Павленко Вячеслав Николаевич __________________________________   «___» _________ 2016 г.

Научный руководитель Соколинская Ирина Михайловна Доцент Кандидат физико-математических наук __________________________________   «___» _________ 2016 г.

 

Челябинск

Содержание

Введение............................................................................................................. 3

1.Сеточный алгоритм........................................................................................ 4

... 1.1.Постановка задачи................................................................................... 4

... 1.2.Идея алгоритма....................................................................................... 5

... 1.3.Построение сеточной области................................................................. 8

... 1.4.Пересечение многогранника M с ячейкой 𝛼...................................................... 10

2.Схема сеточного алгоритма............................................................................................ 12

.... 2.1.Схема головной подпрограммы.......................................................................... 12

2.2.Схема подпрограммы инициализации переменных init........................ 16

... 2.3.Схема подпрограммы вычисления псевдопроекции............................. 18

3.Модельный пример........................................................................................ 22

4.Полученные результаты................................................................................ 24

Список литературы........................................................................................... 25

Приложение 1

Приложение 2

 

Введение

В практике экономико-математического моделирования встречаются задачи линейного программирования большой размерности. Часто подобные задачи характеризуются изменениями исходных данных в процессе нахождения решения, что придает им вид явно нестационарных. Существующие методы не применимы, либо мало эффективны при решении задач линейного программирования большой размерности при быстро меняющихся исходных данных. Хорошо адаптируются к изменяющимся исходным данным фейеровские отображения, однако они обладают медленной сходимостью. Перспективным является подход, сочетающий использование фейеровских отображений для вычисления проекций на меняющийся выпуклый многогранник с их эффективным распараллеливанием на кластерных вычислительных системах с многоядерными ускорителями. Результаты, которые ожидаемо может дать предлагаемый подход, могут превзойти по эффективности все известные в настоящее время методы при решении нестационарных задач линейного программирования большой размерности.

 

Сеточный алгоритм

Постановка задачи

Пусть задана задача линейного программирования

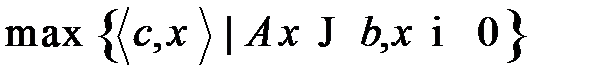
Определим фейеровское отображение следующим образом:

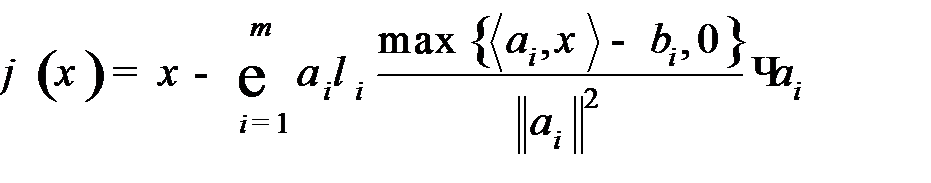
Пусть M – многогранник, задаваемый ограничениями задачи линейного программирования. Такой многогранник всегда является выпуклым. Известно [10], что будет однозначным непрерывным M -фейеровским отображением для любой системы положительных коэффициентов , таких, что , и коэффициентов релаксации . Полагая в формуле и , получаем формулу

,

которая будет использоваться в сеточном алгоритме.

Обозначим

.

Под фейеровским процессом, порождаемым отображением при произвольном начальном приближении , будем понимать последовательность . Известно, что указанный фейеровский процесс сходится к точке, принадлежащей множеству M:

.

Будем кратко обозначать это следующим образом: .

Под - проектированием (псевдопроектированием) точки на многогранник M понимается отображение .

 

Идея алгоритма

В общем виде сеточный алгоритм может быть описан следующим образом. Все пространство 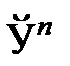делится гиперкубической сеткой на ячейки с переменной длиной грани. Размер ячейки может динамически меняться в зависимости от скорости изменения исходных данных: чем быстрее меняются данные, тем больше становится ячейка, чтобы успевать следить.

Алгоритм постоянно находит (отслеживает) ячейку наименьшего размера, на которой достигается максимум целевой функции. Будем такую ячейку называть целевой. В каждой итерации алгоритма просчитываются ячейки, входящие в некоторую сеточную область вокруг целевой ячейки.

Рис. 1. Сеточная область кубической формы с целевой ячейкой в центре.

В простейшем случае сеточная область может быть кубической формы со следящей ячейкой в центре. В общем случае сеточная область может быть произвольной выпуклой фигурой. При этом ячейки всегда имеют кубическую форму.

Целевая точка – это некоторая точка, находящаяся вне сеточной области. Ее координаты могут динамически вычисляться по коэффициентам целевой функции. Например, при целевой функции в качестве целевой точки можно взять точку (T, 2 T), где T – достаточно большое положительное число.

Нулевой вершиной кубической области будем называть вершину куба, находящуюся ближе всего к началу координат. Нулевой вершиной кубической ячейки будем называть вершину ячейки, находящуюся ближе всего к началу координат.

Неформально сеточный алгоритм может быть описан следующей последовательностью действий.

1. Первоначально выбирается сеточная кубическая область с длиной ребра r и нулевой вершиной в точке g, заведомо покрывающая многогранник M.

2. Выбирается целевая точка , расположенная вне сеточной области.

3. Сеточная область разбивается на K ячеек.

4. В условиях динамического изменения входных данных (A, b, c) для всех ячеек внутри сеточной области вычисляется псевдопроекция из точки z на пересечение ячейки с многогранником M. Если пересечение пусто, то такие ячейки отбрасываются.

5. Если получено пустое множество псевдопроекций, то мы увеличиваем размер сеточной области в w раз и переходим на шаг 2.

6. Если получено непустое множество псевдопроекций, то на нем вычисляется максимум целевой функции.

7. Если расстояние от точки максимума до центра сеточной области меньше , то длина ребра сеточной области r уменьшается в 2 раза.

8. Если расстояние от точки максимума до центра сеточной области больше , то длина ребра сеточной области r увеличивается в 1.5 раза.

9. Центр сеточной области перемещается в центр ячейки, в которой достигнут максимум, и переходим на шаг 2.

Псевдопроекции на шаге 4 для различных ячеек сеточной области могут вычисляться параллельно без обменов данными между процессами. Фейеровский процесс вычисления псевдопроекции, стартовавший из целевой точки на шаге 4, вычисляется до конца, несмотря на то, что координаты целевой точки и сам многогранник M в процессе счета могли измениться. Выполнение условия шага 5 означает, что входные данные изменяются быстрее, чем мы вычисляем псевдопроекции. Константы и , используемые при выполнении шагов 7 и 8, являются параметрами алгоритма.

 

Построение сеточной области

Без ограничения общности мы можем считать, что все процессы происходят в положительной области координат.

Пусть – размерность пространства решений, – количество ячеек в сеточной области по одному измерению. Пусть 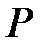– количество MPI‑процессов, используемых для распараллеливания вычислений. Будем предполагать, что всегда выполняется равенство:

,

то есть, количество ячеек сеточной области равно количеству MPI‑процессов.

u 0

u 1

u 2

Рис. 2. Линейная нумерация ячеек сеточной области при n = 3.

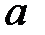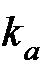Зададим в пространстве целочисленных координат линейную нумерацию ячеек сеточной области следующим образом. Пусть ячейка имеет целочисленные координаты . Тогда ее номер вычисляется по формуле:

.

На рис. 2 приведен пример такой линейной нумерации при . Например, ячейка с номером 19 на рис. 2 имеет целочисленные координаты Действительно, .

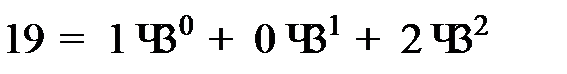Выразим целочисленные координаты ячейки через ее порядковый номер . Из получаем

;

;

;

......

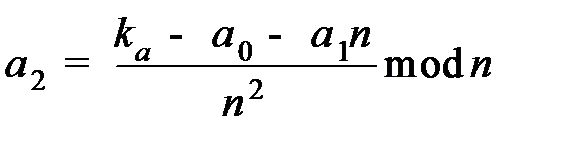Таким образом, в общем виде имеем:

.

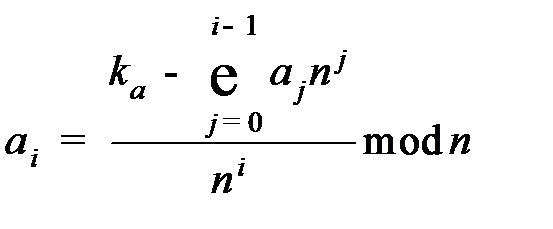Формула содержит ресурсоемкую операцию возведения в степень. От нее можно избавиться следующим образом. По определению операции mod из получаем

[1].

Подставив в вместо правую часть этого уравнения, получим

По определению операции mod отсюда следует

.

Подставив в вместо 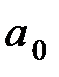правую часть уравнения, а вместо – правую часть уравнения, получим

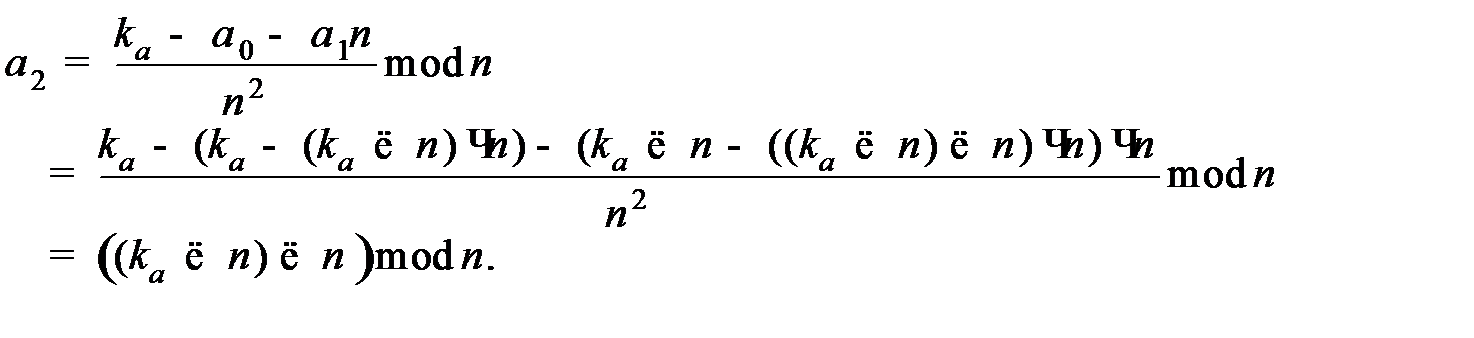
Из и для по индукции получаем:

.

Пусть – нулевая вершина куба сеточной области. Пусть – нулевая вершина произвольной ячейки . Выразим координаты точки y через координаты точки g. Обозначим – шаг сетки. Тогда

.

Определим в качестве центральной ячейки куба ячейку с целочисленными координатами , где

.

Пусть – нулевая вершина центральной ячейки . Выразим координаты точки через координаты точки g, используя формулу:

.

 

1.4. Пересечение многогранника M с ячейкой 𝛼

Пусть – нулевая вершина ячейки 𝛼. Тогда область внутри ячейки 𝛼 (включая границы) задается системой из неравенств:

Эта же система в матричной форме:

,

где (для )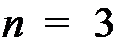

, .

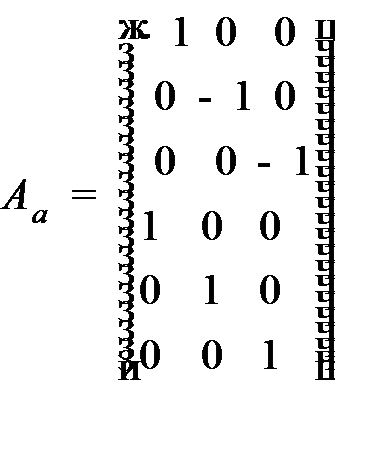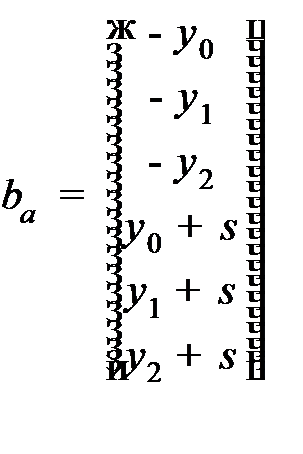Положим

, .

Тогда пересечение многогранника M с ячейкой 𝛼 задается системой неравенств в матричной форме

,

где – расширенная матрица размера , – расширенный столбец свободных членов. Расширенный столбец в соответствии с формулой имеет инвариантную часть b, не зависящую от координат нулевой вершины ячейки 𝛼, и вариативную часть , зависящую от координат нулевой вершины ячейки 𝛼. Элементы расширенной матрицы 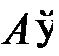не зависят от координат нулевой вершины ячейки 𝛼.

Схема сеточного алгоритма

В данном разделе описывается схема сеточного алгоритма в виде диаграмм деятельности UML. Обозначения, используемые при описании алгоритма, суммированы в приложении 1.