36. Проверка гипотез при полиномиальной аппроксимации: о равноточности измерений, о степени полинома, аппроксимирующего экспериментальные данные (ковариационная матрица погрешностей измерений известна, измерения равноточные и неравноточные).
Полагаем, что известны характеристики погрешностей измерения 
значений 
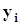аппроксимируемой функции:- при равноточных измерениях - дисперсия 
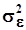,- при неравноточных измерениях - ковариационная матрица 
.
В частном случае ковариационная матрица может быть диагональной, i - ми элементами диагонали являются дисперсии 
погрешностей измерения значений 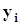аппроксимируемой функции. При каждом значении аргумента 
, i = 1,2,...,k, выполняется n измерений функции. Обозначим результаты этих измерений, через 
, где j -номер эксперимента, j = 1,2,..., n. Вычисляются средние арифметические значения 
,из которых составляется вектор 
, после чего в зависимости от обстоятельств вычисляются МНК(методом наименьших квадратов) или ОМНК(обобщенным -\\-) - оценки коэффициентов аппроксимирующего полинома по формулам п. 2.3.7.2, где вместо вектора 
следует использовать вектор 
. В силу центральной предельной теоремы плотность распределения среднего арифметического стремится к нормальной довольно быстро при любых плотностях распределения исходных погрешностей, которые не слишком сильно различаются по дисперсии (см. п. 1.6.6.4). Поэтому при многократных измерениях требование к нормальности распределения погрешностей измерений значительно смягчается.Как известно из п. 2.3.4.1, дисперсии средних арифметических 
. Точно так же из п. 2.3.4.4 следует, что ковариационная матрица вектора средних арифметических 
. В связи с этими обстоятельствами формулы пп. 2.3.7.2, 2.3.7.3 несколько изменятся.
a) В случае применения МНК.
,
,
но, как и прежде, 
. b) В случае применения ОМНК. 
, 
, 
, 
,но, как и прежде, .
37. Проверка гипотез при полиномиальной аппроксимации: о равноточности измерений, о степени полинома, аппроксимирующего экспериментальные данные (ковариационная матрица погрешностей измерений неизвестна, измерения равноточные и неравноточные).
При многократных измерениях предоставляется возможность оценить дисперсии при каждом i: 
или ковариационную матрицу в целом.Корректная оценка всех элементов ковариационной матрицы , не только диагональных, но и внедиагональных возможна лишь при выполнении специально организованного эксперимента.Выполняется один цикл измерений в такой последовательности:- воспроизводится значение физической или иной величины, соответствующее первому значению аргумента 
и выполняется измерение (определение) значения функции, полученный результат - 
,- воспроизводится значение физической или иной величины, соответствующее второму значению аргумента 
и выполняется измерение (определение) значения функции, полученный результат - 
,- описанная процедура продолжается до достижения последнего, k - го значения аргумента х, таким образом будет получен первый вектор результатов измерений 
,- устанавливается значение физической величины x, превышающее значение 
, затем вновь устанавливается значение , и процесс повторяется, но в обратном порядке, при уменьшении значений x; таким образом будет получен второй вектор результатов 
,- в конечном итоге так будет получено четное количество n векторов вида 
, j = 1, 2,..., n. По этому массиву экспериментальных данных вычисляются оценки (см. пп. 2.3.4.3, 2.3.4.4): 
, 
.Оценка ковариационной матрицы построена в соответствии с ее математическим определением, приведенным в п. 1.7.3. Поскольку при реализации ОМНК эту матрицу придется обращать, она не должна быть особенной. Для этого необходимо, чтобы n > k. Но если по техническим, экономическим или иным причинам это условие выполнить невозможно, то придется ограничиться вычислением только оценок дисперсий 
при каждом значении 
. По этим значениям строится диагональная матрица 
, в диагонали которой на i - ом месте стоит оценка дисперсии . В таком случае не учитывается ковариация между измерениями в точках , что приводит к незначительной потере в эффективности оценок коэффициентов, но они остаютсянесмещенными (см. п.2.3.7.4, замечание 1).
После этого для вычисления оценок коэффициентов аппроксимирующего полинома применяется ОМНК с заменой во всех формулах п. 2.3.7.5 матрицы на : 
, 
, 
, 
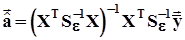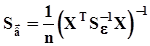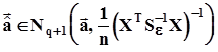.Вследствие случайности исходных данных величина 
также случайна. Из-за участия в формуле для 
вместо генеральной ковариационной матрицы ее оценки в данном случае распределение “хи - квадрат” неприменимо. Вместо него здесь применяется плотность F - распределения Фишера (иногда она именуется, как плотность распределения Фишера - Снедекора), и обозначается, как 
, где 
и 
- количества степеней свободы. Плотность распределения Фишера имеет случайная величина [5] F = 
,что записывается в виде F = 
.Нетрудно увидеть, что величина также, в некотором смысле есть отношение дисперсий. Функция распределения Фишера табулирована, таблицы приводятся в специальных таблицах математической статистики (например, [1,13, 14]). Из последних выражений для величины F следует, что при подготовке эксперимента по аппроксимации зависимостей необходимо обеспечивать выполнение неравенства n > k - q -1, то есть превышение количества повторных измерений над числом степеней свободы квадратичной формы 
. Иногда по техническим, экономическим или иным объективным причинам это условие оказывается невыполнимым. В таком вынужденном случае придется формировать диагональную матрицу : 
, , и применять ее при вычислении оценок коэффициентов.В этой ситуации F - распределению Фишера подчиняется случайная величина F = 
.Число степеней свободы k - q - 1 и n - 1. В частном случае, когда по результатам проверки по критерию Кочрена (п. 2.5.6.1) гипотезы о равенстве дисперсий будет принято решение о применении МНК, тогда вычисляется средняя оценка дисперсии 
,которая подставляется вместо 
во всех соответствующих формулах п. 2.3.7.5: 
, 
,И в этом случае случайная величина F = .распределена в соответствии с F - распределением Фишера с числом степеней свободы k - q - 1 и n - 1.
38.Обусловленность задачи полиномиальной аппроксимации, методы обеспечения устойчивости решения 2.3.7.7. Особенности вычислений при реализации МНК и ОМНК Как следует из пп. 2.3.7.2, 2.3.7.3, в процессе оценивания коэффициентов аппроксимирующих полиномов приходится обращать матрицы 
и 
. Из линейной алгебры и вычислительной математики известно, что устойчивость результатов подобных действий в сильной степени зависит от обусловленности обращаемых матриц. Что касается матриц 
и , то здесь следует опасаться того, что они могут оказаться особенными. В частности, одна из причин появления особенности у матрицы указана в предыдущем пункте.Обусловленность матриц характеризуется числом обусловленности, которое есть не что иное, как коэффициент “усиления” погрешностей экспериментальных данных и погрешностей округления к погрешностям результатов вычислений. Для квадратных симметричных матриц, каковыми являются матрицы, перечисленные выше, число обусловленности определено равенствами 
, 
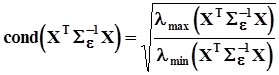где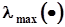 
, 
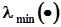- наибольшее и наименьшее собственные числа соответствующей матрицы. Число обусловленности матриц, используемых в МНК или в ОМНК, может достигать значений 
и выше.Известно, что число обусловленности указанных матриц монотонно возрастает с увеличением количества столбцов матрицы X, то есть с увеличением порядка q или, что то же самое, с увеличением числа коэффициентов полинома (см. конструкцию матрицы X в п. 2.3.7.2). Максимального значения число обусловленности достигает при q + 1 = k. Особенно опасной оказывается ситуация, когда количество оцениваемых коэффициентов превышает их фактическое количество, то есть при завышении степени полинома. Можно рекомендовать три способа повышения устойчивости оценок коэффициентов МНК и ОМНК.
1. Не стремиться к излишне высокому порядку аппроксимирующего полинома, использовать априорную информацию о гладкости аппроксимируемой функции. 2. При необходимости аппроксимации функции y = f(x) полиномом высокого порядка вплоть до q = k - 1 использовать метод регуляризации А.Н.Тихонова.Применительно к МНК и ОМНК этот метод заключается в следующем [7].Исходное уравнение преднамеренно искажается таким образом, чтобы это искажение заведомо улучшало обусловленность. Таким регуляризирующим искажением является, по Тихонову, увеличение диагональных элементов матрицы системы уравнений. Регуляризированное таким образом решение имеет вид 
.
|
Число a называется параметром регуляризации. Оценка 
называется ридж-оценкой. В отечественной литературе встречается калькоподобный.Эта оценка, конечно, смещена. Ее смещение примерно равно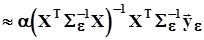 
.Проблема состоит в выборе такого значения параметра регуляризации, при котором результирующая погрешность, вызванная смещением оценки и плохой обусловленностью матрицы системы, была минимальной.На рис. показана принципиальная возможность такого выбора. Однако, универсального практического рецепта выбора оптимального значения параметра регуляризации пока не существует. 3. Третий способ заключается в таком размещении значений аргумента x, при котором число обусловленности матрицы или было минимальным. Основные принципы планирования эксперимента, выполняемого с целью полиномиальной аппроксимации. Снова обратимся к конструкции матрицы X, приведенной в п. 2.3.7.2, и к одной из формул вычисления ковариационной матрицы оценок коэффициентов полинома, например, 
. Из конструкции матрицы X видно, что ее элементы изменяют свои значения в зависимости от значений аргумента полинома: 
. Стало быть, можно надеяться на то, что существует такой план расстановки этих значений, при котором погрешности в каком-либо смысле будут минимальными. Такие планы, действительно, существуют. Назовем некоторые из них. А - оптимальный план эксперимента - план, при котором достигается min следа матрицы 
, то есть min суммы ее диагональных элементов. D - оптимальный план эксперимента - план, при котором достигается min значение определителя матрицы . С - оптимальный план эксперимента - план, при котором достигается min значение числа обусловленности матрицы . С - оптимальный план эквивалентен D - оптимальному плану. Расширение класса аппроксимирующих полиномов. Материал, изложенный выше, в равной степени относится к оценке коэффициентов обобщенных аппроксимирующих полиномов с заменой понятия “степень полинома” на “порядок полинома”. Обобщенным полиномом называется полином вида 
, 
- система базисных функций.Если эти ф-и ортогональны и соответствуют характеру аппроксимируемой зависимости лучше, чем степени x, то для достижения необходимой точности аппроксимации может понадобиться меньше членов, чем в случае аппроксимации степенным полиномом. А это обстоятельство способствует улучшению обусловленности задачи и является четвертым средством повышения устойчивости оценок МНК и ОМНК.Матрица X в этом случае будет иметь следующую конструкцию: 
.Это единственное отличие от изложенного выше.
39. Интервальные оценки, их практическое значение и преимущества перед точечными, понятие доверительной вероятности, доверительные интервалы для математического ожидания (дисперсия генеральной совокупности известна и неизвестна).
Целью интервального оценивания является вычисление по выборочным данным 
объема n такого интервала с границами: нижней - 
и верхней 
, чтобы 
,где Q - вероятность, близкая к единице, например Q = 0.8 ¸ 0.95. Такой интервал называется доверительным интервалом (confidenceinterval), вероятность Q - доверительной вероятностью. Границы доверительного интервала являются функциями выборочных значений, они случайны. Поэтому говорят, что доверительный интервал накрывает значение искомой генеральной характеристики (параметра) с вероятностью, не меньшей, чем Q. Пусть выборка 
извлечена из нормальной генеральной совокупности, образованной случайной величиной 
, 
известна. Несмещенная, состоятельная и эффективная точечная оценка математического ожидания - среднее арифметическое 
.Это линейная функция выборочных значений, извлеченных из нормальной генеральной совокупности, нормальное распределение безгранично делимо, поэтому 
распределено нормально: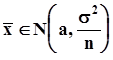 
.Вычтем из его математическое ожидание и разделим результат на его среднеквадратическое значение. Получим новую случайную величину, которая также нормально распределена: 
.Пусть 
- a×100 - процентная квантиль,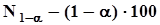 
- процентная квантиль нормального распределения. Вероятностная мера интерквантильного промежутка 
есть
.
Пусть Q - доверительная вероятность, 
, 
. В силу симметрии нормального распределения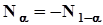 
. 
.Следует обратить пристальное внимание на две тенденции поведения границ доверительного интервала: 1. С увеличением объема выборки при фиксированном значении доверительной вероятности ширина доверительного интервала уменьшается и в пределе стремится к нулю, что вполне естественно. 2. При фиксированном значении объема выборки с увеличением доверительной вероятности ширина доверительного интервала увеличивается, и в пределе при Q = 1 доверительным интервалом становится вся ось, что также вполне естественно, ибо для покрытия неизвестного значения с большой вероятностью требуется широкий интервал. Дисперсия генеральной совокупности неизвестна. Пусть как и ранее, , 
. Поскольку дисперсия неизвестна, будем использовать ее несмещенную оценку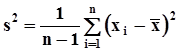 
.По аналогии с п. 2.4.3 сформируем случайную величину 
.Плотность распределения этой случайной величины есть плотность распределения.Стъюдента с (n – 1) степенью свободы, которая имеет следующий вид: 
.Это одномодальная симметричная плотность распределения. При значительных объемах выборки n математическое ожидание, дисперсия и эксцесс случайной величины τ, распределенной по Стъюденту, равны:
.Единственный параметр плотности распределения Стъюдента - число степеней свободы.
Частный вид плотности распределения Стъюдента при n = 2 - плотность распределения Коши. При n ®¥ плотность распределения Стъюдента стремится к нормальному распределению. Удовлетворительная близость к нормальному распределению начинается уже с n = 20. Квантили распределения Стъюдента с числом степеней свободы (n - 1): 
и 
- суть границы интерквантильного промежутка, такого, что
В силу симметрии плотности распределения Стъюдента
= - .С учетом этого факта и выражая вероятность a через Q, решим неравенство, стоящее в скобках, относительно a: 
.Получен доверительный интервал для математического ожидания в условиях, когда вместо дисперсии применяется ее несмещенная оценка.
В этом случае также проявляется полезное свойство центральной предельной теоремы, позволяющее при значительных объемах выборки (начиная с n = 20) пользоваться полученным доверительным интервалом для оценки математического ожидания широкого класса наиболее употребительных случайных величин, плотность распределения которых отличается от нормальной.
Как и в предыдущем пункте, обращаем внимание на две тенденции поведения границ доверительного интервала:
1. С увеличением объема выборки при фиксированном значении доверительной вероятности ширина доверительного интервала уменьшается и в пределе стремится к нулю, что вполне естественно.
2. При фиксированном значении объема выборки с увеличением доверительной вероятности ширина доверительного интервала увеличивается, и в пределе при Q = 1 доверительным интервалом становится вся ось, что также вполне естественно, ибо для покрытия неизвестного значения с большой вероятностью требуется широкий интервал.
40. Параметрические доверительные интервалы для дисперсии и для интерквантильного промежутка.
Пусть как и ранее, . Математическое ожидание неизвестно, для его оценки применено среднее арифметическое . Точечная несмещенная оценка дисперсии .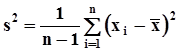
|
В п. 2.3.4.2 с) мы выяснили, что плотность распределения случайной величины 
есть плотность распределения 
с (n - 1) степенями свободы. Квантили этой плотности распределения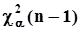 
и 
суть границы интерквантильного промежутка, который определяется равенством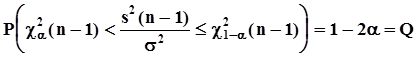 
.
Как видно из рис. 33 и из рис. 28 п. 2.3.4.2 с), плотность распределения “хи - квадрат” несимметрична, поэтому после решения неравенства, стоящего в скобках, получим доверительные интервалы с несимметричными границами:
,
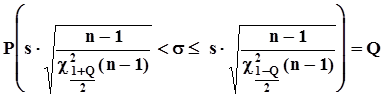.Расположение квантилей, использованных в этих формулах, показано на рис. 33. Материалы настоящего пункта справедливы только для случаев, когда выборка извлечена из нормальной генеральной совокупности. Доверительные интервалы для интерквантильного промежутка.