Тема 8
Математическое моделирование движения космических аппаратов
Многообразие видов космической техники объединяет теория их движения. В отличие от наземных механических систем, движение которых можно изучать экспериментально, движение космических аппаратов исследуется в основном с помощью математических моделей.
Как свидетельствуют многие факты, дошедшие до нас из глубин истории, уже в те давние времена были известны модели движения Солнца, Луны, некоторых планет солнечной системы, звезд и комет, которые позволяли с высокой точностью прогнозировать реальное движение этих небесных тел.
В начале 17 века Кеплер, анализируя результаты наблюдений Марса, проведенных астрономом Тихо де Браго, установил ряд законов движения небесных тел. Знаменитый математик и механик Исаак Ньютон показал обще-механический смысл законов Кеплера, первоначально имевших чисто эмпирический характер.
В начале прошлого столетия выдающиеся русские ученые, такие, как Циолковский, Мещерский, Цандер, заложили основы теории движения космических аппаратов (КА) на всех этапах их полета в ближний и дальний космос. Многие идеи этих ученых до сих пор широко используются при создании современной космической техники.
Последние достижения в математике, механике, в теории управления, кибернетике и вычислительной технике позволяют создать разветвленную систематизированную сеть математических моделей движения КА, различного назначения и точности.
В традиционных учебниках по формированию математических моделей управляемого движения КА рассматриваются:
- уравнения реактивного движения КА (в инерциальной и неинерциальной системах отсчета);
- основные понятия теория моделирования движения;
- общие представления о различных динамических системах, нашедших широкое применение в практике моделирования управляемого движения КА;
- основные задачи управления движением динамических систем: задача управляемости и задача оптимального управления;
- задача создания рациональной динамической системы, моделирующей с требуемой точностью управляемое движение КА;
- методы и алгоритмы формирования математической модели движения, основанные на сравнительном анализе ее точности;
- методика и принципы определения области применения (действия) сформированной модели.
Математическая модель движения КА
Принцип движения посредством создания реактивной силы известен с незапамятных времен, однако идея его использования длякосмических полетов принадлежит русскому ученому — энтузиасту К.Э. Циолковскому, которыйразработал и впервые применил для практических расчетов математическую модель реактивного движения КА.
Согласно основным теоремам механики движение любого жесткого тела можно представить, как совмещение двух движений:
· движение центра масс (ц.м.) тела;
· движение относительно (вокруг) ц.м.
Формально это можно представить в виде двух векторных дифференциальных уравнений:
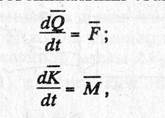
где Q, К — количество движения и момент количества движения жесткого тела, соответственно; F, М — сила и момент силы, действующие на тело соответственно (черта над символами обозначает векторные величины).
Однако поскольку речь идет о моделирование движения КА, а его активный полет совершается, как правило, посредством использования реактивных двигателей, которые в процессе своей работы существенно изменяют массу КА, поэтому изменение количества движения и момента количества движения КА будут происходить не только под действием силы F и момента М, как это показано в приведенных уравнениях.
Считая, что относительное движение КА вокруг его ц.м. никак не влияет на изменение количества движения КА, рассмотрим его движение как движение материальной точки переменной массы, сосредоточенной в ц.м. КА.
Движение КА как материальной точки переменной массы
Пусть в момент времени t скорость ц.м. КА и его масса имели значение v и m, соответственно. Тогда его количество движения
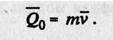
И пусть за малое время Dt точка массой m(t) «отделяет» частицы массой Dm1. Тогда можно записать, что в момент времени t+Dt общее количество движения материальной точки и отделенных частиц будет
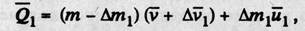
где Dv 1 — изменение скорости точки, отделившей к моменту t+Dt частицы массой Dm1; и1 — абсолютная скорость отделяемых точкой частиц (см. рис.).
Согласно закону сохранения количества движения, считая, что на материальную точку никаких сил не действует, имеем
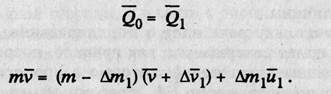
Пренебрегая величинами второго порядка малости (Dt мало), получаем:
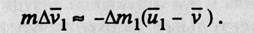
Отсюда можно определить изменение скорости материальной точки, отделяющей частицы:
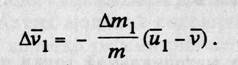
Если разделить левую и правую части соотношения на Dt, а затем перейти к пределу:
,
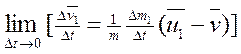можно получить выражение для ускорения точки в виде
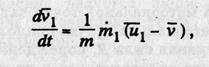
где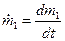 
— секундный расход массы (понятно, что 
).
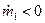Проводя аналогичные рассуждения для ускорения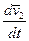 
(в случае присоединения частиц к массе), можно получить соотношение вида
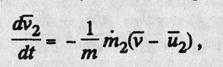
где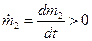 
— интенсивность увеличения массы точки; и — абсолютная скорость присоединяющихся частиц.
Согласно второму закону Ньютона изменение количества движения материальной точки постоянной массы Dv3 может происходить
под действием силы F, (действующей некоторое малое время).
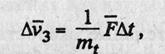
где mt -— масса материальной точки в момент времени t, которая остается постоянной до момента t+Dt.
Переходя к пределу:
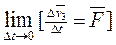, можно записать:
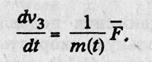
Поскольку в реальности масса материальной точки из-за непрерывного отделения частиц все время меняется, то указанные уравнения нельзя непосредственно связывать. Чтобы это стало возможным был сформулирован основной принцип реактивного движения, позволяющий совместить изменение количества движения, как за счет изменения массы, так и вследствие действия внешних сил.
Принцип затвердевания массы материальной точки. Уравнение движения материальной точки с переменной массой в произвольный момент времени может быть представлено как уравнение движения этой же точки с фиксированной массой, если считать, что в этот момент времени масса материальной точки «затвердела» и что к полученной фиктивной материально точке приложены не только внешняя сила F но и фиктивная сила R, порожденная изменением количества движения за счет отделяющихся и присоединяющихся с определенными скоростями частиц.
Таким образом, появляется возможность объединить три составляющих изменения скорости материальной точки и полное ускорение движущейся под действием внешней силы «тяжелой» точки переменной массы можно представить в виде
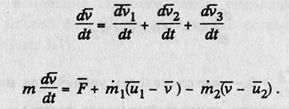
Полученное уравнение носит имя известного русского механика И.В. Мещерского.
Если ввести новые обозначения
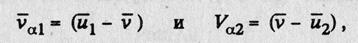
определяющие относительные скорости отделения и присоединения частиц, соответственно, то обобщенное уравнение Мещерского можно переписать:
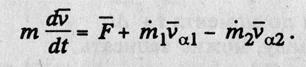
При исследовании движения подавляющего большинства КА можно принять относительную скорость присоединяющихся масс равной нулю. Тогда это уравнение примет вид
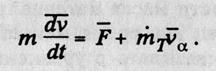
где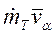 
— секундный расход рабочего тела (топлива).
Слагаемое 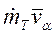имеет размерность силы и определяется как реактивная сила R. С учетом этого уравнение можно переписать в виде
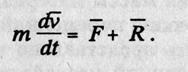
Полученное векторное дифференциальное уравнение является формальным отображением принципа затвердевания материальной точки, движущейся под действием внешней и реактивной сил.
Вместе с начальными условиями это дифференциальное уравнение образует так называемую динамическую систему, которая является математической моделью движения тяжелой материальной точки под действием различных сил (движение ц.м. тела).
Силы, учитываемые при моделировании движения КА
По сложившейся традиции математическое моделирование движения различных тел является целью и предметом исследования трёх наук: теоретической механики, баллистики и динамики движения различных тел, в том числе и КА.
К сожалению, не существует достаточно точных и установившихся определений этих наук, однако в настоящее время в этом нет никакой необходимости, поскольку с позиции более строгого, математического подхода облик конкретной модели движения определяется требованиями точности моделирования, а не принадлежностью разрабатываемой модели к той или иной названной науке.
На любое физическое тело воздействует бесконечное множество сил, имеющих различную природу и отличающихся по величине и направлению. Не вызывает сомнения, что, чем большее их число, будет учтено в математической модели, тем точнее она будет отображать реальный процесс.
В то же время известно, что с ростом количества учитываемых сил возрастает сложность и «громоздкость» математической модели, приводя в итоге к снижению её компьютерной эффективности. Следовательно, необходимо стремиться к минимальному составу учитываемых сил без ущерба для точности математической модели.
Другими словами, рациональные или оптимальные математические модели должны учитывать ровно столько действующих на КА сил, сколько необходимо для обеспечения требуемой точности моделирования.
Основные силы, действующие на КА в полете
При моделировании различных этапов полета КА в солнечной системе рекомендуется учитывать следующие силы (на начальных стадиях проектирования космического комплекса):
А) ВНЕШНИЕ СИЛЫ
- гравитационные силы Солнца, планет солнечной системы, спутников планет и других небесных тел (определяющие науки: Математика, Физика, Теоретическая механика, Баллистика, Динамика полета, Статистическая динамика);
- аэродинамические силы, действующие на КА при полете в атмосферах планет (определяющие науки: Математика, Физика, Аэродинамика, Динамика полета, Статистическая динамика);
- силы давления различных излучений, например световое давление от Солнца (определяющие науки: Математика, Физика, Баллистика, Динамика полета, Статистическая динамика);
- силы одиночных столкновений с микрометеоритами, космической пылью и с искусственными объектами (определяющие науки: Математика, Физика, Баллистика, Динамика полета, Статистическая динамика).
Б) ВНУТРЕННИЕ СИЛЫ
- различные реактивные силы, обусловленные перемещением, вращением или колебанием массивных тел (твердых, жидких, газообразных) внутри КА (определяющие науки: Математика, Физика, Динамика полета, Статистическая динамика);
- кориолисовы силы, возникающие в результате взаимодействия вращения корпуса КА и внутреннего движения различных тел, жидкостей и газов (определяющие науки: Математика, Физика, Теоретическая механика, Динамика полета, Статистическая динамика);
В) СИЛЫ ТЯГИ (давления), создаваемые различными движителями:
- двигательными установками, работающими на химических компонентах рабочего тела (топлива) (определяющие науки: Математика, Физика, Динамика полета, Статистическая динамика);
- электрореактивными двигательными установками, использующими мощное электрическое поле (определяющие науки: Математика, Физика (Электричество), Динамика полета);
- солнечными парусами (определяющие науки: Математика, Физика, Динамика полета, Статистическая динамика).
Каждая из перечисленных сил или групп сил имеет свою физическую и математические модели разной точности. По существу, каждая модель силы разрабатывается на основе отдельной науки либо направления науки, либо соответствующей теории.
Например, моделированию аэродинамических сил, действующих на КА посвящена целая наука аэродинамика, имеющая много разветвлений и разделов, которые развивались в соответствии с множеством моделей аэродинамических сил, действующих в различных средах, на различных скоростях движения КА и на аппараты различной формы.
