Арифметические операции сложения и вычитания в дополнительном коде

Основным достоинством дополнительного кода является то, что в нем единообразно реализуются операции сложения чисел разных знаков (алгебраическое сложение), а операцию вычитания можно свести к операции сложения заменой знака вычитаемого на обратный.

Пример_38: Сложение в обратном коде чисел 2₍₁₀₎ и -5₍₁₀₎.

Код	2(10)	-5(10)
Прямой	0000 0010(2)	1000 0101(2)
Обратный	0000 0010(2)	1111 1010(2)
Дополнительный	0000 0010(2)	1111 1011(2)

 

 

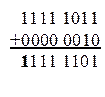
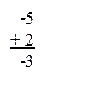
Так как результат сложения является кодом отрицательного числа (знак 1), то переведем дополнительный код в обратный: 1111 1100₍₂₎, а обратный код 1111 1100₍₂₎ в прямой: 1000 0011₍₂₎, что соответствует числу -3.

Пример_39: Сложение в обратном коде чисел 7₍₁₀₎ и -1₍₁₀₎.

Код	7(10)	-1(10)
Прямой	0000 0111(2)	1000 0001(2)
Обратный	0000 0111(2)	1111 1110(2)
Дополнительный	0000 0111(2)	1111 1111(2)

 

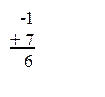
Так как результат сложения является кодом положительного числа (знак 0), то дополнительный код 1111 1110₍₂₎ соответствует прямому коду числа 6₍₁₀₎.

Кодирование текстовой информации.

Поскольку текст изначально дискретен (он состоит из отдельных символов) для компьютерного представления текстовой информации используется способ, когда все символы кодируются числами, и текст представляется в виде набора чисел – кодов символов, его составляющих. При выводе текста на экран монитора или принтера необходимо восстановить изображения всех символов, составляющих данный текст. Для этого используются так называемые кодовые таблицы символов, в которых каждому коду символа ставится в соответствие изображение символа.

Кодовая таблица – это внутреннее представление символов в компьютере.

Во всем мире в качестве стандарта принята таблица ASCII (American Standard Code for Information Interchange – Американский стандартный код для обмена информацией). Для хранения двоичного кода одного символа выделен 1 байт = 8 бит. Учитывая, что каждый бит принимает значение 0 или 1, количество их возможных сочетаний в байте равно 2⁸ = 256. Значит, с помощью 1 байта можно получить 256 разных двоичных кодовых комбинаций и отобразить с их помощью 256 различных символов.

Эти комбинации и составляют таблицу ASCII. Эта таблица состоит из 16 строк и 16 столбцов, пронумерованных от 0 до F в 16-ричной системе счисления.

Например, в столбце 4 и строке D таблицы расположена заглавная буква М латинского алфавита. Таким образом, при записи текста с такой буквой, она будет храниться в памяти в виде кода 4D(16) или 77(10). Другие коды: "," – 2C; "j" – 6A; "2" – 32. Такая форма кодирования позволяет представлять буквы в более компактном виде по сравнению с двоичным кодом.

Первые 8 столбцов таблицы кодов или первые 128 символов от 0 (двоичный код 00000000) до 127 (01111111) – цифры, буквы латинского алфавита, управляющие символы. Первые 32 символа являются управляющими и предназначены в основном для передачи команд управления. А последние 8 столбцов таблицы кодов, т.е. коды от 128 (двоичный код 10000000) до 255 (11111111) обычно содержат буквы национальных алфавитов, графические знаки. В большом количестве разновидностей таблицы кодов ASCII первая половина таблицы является неизменной, а вторая - переменной.

Однако 8-битовая кодировка (2⁸) является недостаточной для кодировки всех символов расширенных алфавитов. Все препятствия могут быть сняты при переходе на 16-битовую (2¹⁶) кодировку Unicode, допускающую 65536 кодовых комбинаций.

Необходимо помнить, что в настоящее время для кодировки русских букв используют пять различных кодовых таблиц (КОИ - 8, СР1251, СР866, Мас, ISO), причем тексты, закодированные при помощи одной таблицы, не будут правильно отображаться в другой кодировке. Наглядно это можно представить в виде фрагмента объединенной таблицы кодировки символов.

Одному и тому же двоичному коду ставится в соответствие различные символы.

Пример:

Двоичный код	Десятичный код	КОИ8	СР1251	СР866	Мас	ISO
		б	В	-	-	Т

Впрочем, в большинстве случаев о перекодировке текстовых документов заботится не пользователь, а специальные программы – конверторы, которые встроены в приложения.

Начиная с 1997 г. последние версии Microsoft Windows&Office поддерживают новую кодировку Unicode. Чтобы определить числовой код символа можно или воспользоваться кодовой таблицей, или, работая в текстовом редакторе MS Word. Для этого в меню нужно выбрать пункт «Вставка» – «Символ», после чего на экране появляется диалоговая панель «Символ». В диалоговом окне появляется таблица символов для выбранного шрифта. Символы в этой таблице располагаются построчно, последовательно слева направо, начиная с символа Пробел (левый верхний угол) и, кончая, буквой «я» (правый нижний угол).

Для определения числового кода символа в кодировке Windows (СР1251) нужно при помощи мыши или клавиш управления курсором выбрать нужный символ, затем щелкнуть по кнопке Клавиша. После этого на экране появляется диалоговая панель Настройка, в которой в нижнем левом углу содержится десятичный числовой код выбранного символа.

 

Вопросы для самоконтроля

1. Что изучает дисциплина информатика?

2. Дайте определение понятию «информация».

3. Формы представления информации.

4. Перечислите свойства информации.

5. Какова минимальная единица измерения информации?

6. Какова основная единица измерения информации?

7. Как задаются производные единицы измерения информации?

8. Дайте определение понятию «количество информации».

9. Как связаны между собой понятия «энтропия» и «информация»?

10. Что измеряет синтаксическая мера информации?

11. Что измеряет семантическая мера информации?

12. Что измеряет прагматическая мера информации?

13. Дайте определение понятию «система счисления».

14. Чем отличается позиционная система счисления от непозиционной?

15. Приведите примеры позиционной и непозиционной систем счисления.

16. В какой системе счисления при представлении числа используются буквы латинского алфавита?

17. Как представляются данные в компьютере?

18. Для чего используется кодовая таблица?

19. Как кодируются символы в памяти компьютера?

20. Что собой представляет таблица ASCII кодов?

21. Как определить числовой код символа?

22. Представление целых положительных и отрицательных чисел в прямом, обратном и дополнительном кодах.

23. Правила сложения и вычитания положительных и отрицательных чисел в обратном коде.

24. Правила сложения и вычитания положительных и отрицательных чисел в дополнительном коде.