Арифметические операции в двоичной системе счисления

В таблице 3 представлены операции сложения, вычитания и умножения в двоичной системе счисления.

Таблица 3

Арифметические операции в двоичной системе счисления

Сложение	Вычитание	Умножение
0+0=0	0-0=0	0*0=0
1+0=1	1-0=1	1*0=0
0+1=1	0-1=1	0*1=0
1+1=10	1-1=0	1*1=1

Примечание: При сложении двух чисел, равных 1, в данном разряде получается 0, а 1-ца переносится в старший разряд.

Пример_21: Даны числа 101₍₂₎ и 11₍₂₎. Найти сумму этих чисел.

,

где 101₍₂₎= 5₍₁₀₎, 11₍₂₎= 3₍₁₀₎, 1000₍₂₎ = 8₍₁₀₎.

Проверка: 5+3=8.

При вычитании из 0 единицы, занимается единица из старшего ближайшего разряда, отличного от 0. При этом, единица занятая в старшем разряде, даёт 2 единицы в младшем разряде и по единице во всех разрядах между старшим и младшим.

Пример_22: Даны числа 101₍₂₎ и 11₍₂₎. Найти разность этих чисел.

,

где 101₍₂₎=5₍₁₀₎, 11₍₂₎=3₍₁₀₎, 10₍₂₎=2₍₁₀₎.

Проверка: 5-3=2.

Операция умножения сводится к многократному сдвигу и сложению.

Пример_23: Даны числа 11₍₂₎ и 10₍₂₎. Найти произведение этих чисел.

 

* 10

11

110,

 

где 11₍₂₎=3₍₁₀₎, 10₍₂₎=2₍₁₀₎, 110₍₂₎=6₍₁₀₎.

Проверка: 3*2=6.

 

Арифметические операции в восьмеричной системе счисления

При сложении двух чисел, в сумме равных 8, в данном разряде получается 0, а 1-ца переносится в старший разряд.

Пример_24: Даны числа 165₍₈₎ и 13₍₈₎. Найти сумму этих чисел.

,

где 165₍₈₎= 117₍₁₀₎, 13₍₈₎= 11₍₁₀₎, 200₍₈₎ = 128₍₁₀₎.

При вычитании из меньшего числа большего, занимается единица из старшего ближайшего разряда, отличного от 0. При этом, единица занятая в старшем разряде, даёт 8 в младшем разряде.

Пример_25: Даны числа 114₍₈₎ и 15₍₈₎. Найти разность этих чисел.

,

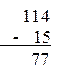где 114₍₈₎=76₍₁₀₎, 15₍₈₎=13₍₁₀₎, 77₍₈₎=63₍₁₀₎.

 

Арифметические операции в шестнадцатеричной системе счисления

При сложении двух чисел, в сумме равных 16, в данном разряде записывают 0, а 1-ца переносят в старший разряд.

Пример_26: Даны числа 1B5₍₁₆₎ и 53₍₁₆₎. Найти сумму этих чисел.

,

где 1B5₍₁₆₎= 437₍₁₀₎, 53₍₁₆₎= 83₍₁₀₎, 208₍₁₆₎ = 520₍₁₀₎.

При вычитании из меньшего числа большего, занимается единица из старшего ближайшего разряда, отличного от 0. При этом, единица занятая в старшем разряде, даёт 16 в младшем разряде.

Пример_27: Даны числа 11A₍₁₆₎ и 2C₍₁₆₎. Найти разность этих чисел.

,

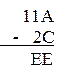где 11A₍₁₆₎=282₍₁₀₎, 2C₍₁₆₎=44₍₁₀₎, EE₍₁₆₎=238₍₁₀₎.

 

Кодирование данных в ЭВМ

Данные в компьютере представляются в виде кода, который состоит из единиц и нулей в разной последовательности.

Код – набор условных обозначений для представления информации. Кодирование – процесс представления информации в виде кода.

Коды чисел

При выполнении арифметических операций в ЭВМ применяют прямой, обратный и дополнительный коды чисел.

Прямой код

Прямой код (представление в виде абсолютной величины со знаком) двоичного числа – это само двоичное число, в котором все цифры, изображающие его значение, записываются как в математической записи, а знак числа записывается двоичной цифрой.

Целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно занимают в памяти один или два байта. Для хранения целых чисел со знаком отводится один, два или четыре байта, при этом старший (крайний левый) разряд отводится под знак числа. Если число положительное, то в этот разряд записывается 0, если отрицательное,- то 1.

Пример_28:

1₍₁₀₎= 0 000 0001₍₂₎, -1₍₁₀₎= 1 000 0001₍₂₎

 

 

Положительные числа в ЭВМ всегда представляются с помощью прямого кода. Прямой код числа полностью совпадает с записью самого числа в ячейке машины. Прямой код отрицательного числа отличается от прямого кода соответствующего положительного числа лишь содержимым знакового разряда.

Прямой код используется при хранении чисел в памяти ЭВМ, а также при выполнении операций умножения и деления, но формат представления чисел в прямом коде неудобен для использования в вычислениях, поскольку сложение и вычитание положительных и отрицательных чисел выполняется по–разному, а потому требуется анализировать знаковые разряды операндов. Поэтому прямой код практически не применяется при реализации в АЛУ арифметических операций над целыми числами. Но отрицательные целые числа не представляются в ЭВМ с помощью прямого кода. Вместо этого формата широкое распространение получили форматы представления чисел в обратном и дополнительном кодах.

Обратный код

Обратный код положительного числа совпадает с прямым, а при записи отрицательного числа все его цифры, кроме цифры, изображающей знак числа, заменяются на противоположные (0 заменяется на 1, а 1 - на 0).

Пример_29:

Код	Положительное число	Отрицательное число
1(10)	-1(10)
Прямой	0000 0001(2)	1000 0001(2)
Обратный	0000 0001(2)	1111 1110(2)

 

Пример_30:

Код	Положительное число	Отрицательное число
5(10)	-5(10)
Прямой	0000 0101(2)	1000 0101(2)
Обратный	0000 0101(2)	1111 1010(2)

 

Для восстановления прямого кода отрицательного числа из обратного кода надо все цифры, кроме цифры, изображающей знак числа, заменить на противоположные.

Дополнительный код

Дополнительный код положительного числа совпадает с прямым, а код отрицательного числа образуется путем прибавления 1 к обратному коду.

Пример_31:

Код	Положительное число	Отрицательное число
6(10)	-6(10)
Прямой	0000 0110(2)	1000 0110(2)
Обратный	0000 0110(2)	1111 1001(2)
Дополнительный	0000 0110(2)	1111 1010(2)

Пример_32:

Код	Положительное число	Отрицательное число
1(10)	-1(10)
Прямой	0000 0001(2)	1000 0001(2)
Обратный	0000 0001(2)	1111 1110(2)
Дополнительный	0000 0001(2)	1111 1111(2)

Пример_33:

Для целого числа -32₍₁₀₎ записать дополнительный код.

1. После перевода числа 32₍₁₀₎ в двоичную систему счисления получим:

32₍₁₀₎=100000₍₂₎.

2. Прямой код положительного числа 32₍₁₀₎ равен 0010 0000.

3. Для отрицательного числа -32₍₁₀₎ прямой код равен 1010 0000.

4. Обратный код числа -32₍₁₀₎ равен 1101 1111.

5. Дополнительный код числа -32₍₁₀₎ равен 1110 0000.

Пример_34:

Дополнительный код числа равен 0011 1011. Найти значение числа в десятичной системе счисления.

1. Первый (знаковый) разряд числа 0 011 1011 равен 0, следовательно, число положительное.

2. У положительного числа дополнительный, обратный и прямой код совпадают.

3. Число в двоичной системе счисления получаем из записи прямого кода – 111011₍₂₎ (нули из старших разрядов отбрасываем).

4. Число 111011₍₂₎ после перевода в десятичную систему счисления равно 59₍₁₀₎.

Пример_35:

Дополнительный код числа равен 1011 1011. Найти значение числа в десятичной системе счисления.

1. Знаковый разряд числа 1 011 1011 равен 1, следовательно, число отрицательное.

2. Для определения обратного кода числа из дополнительного кода вычитаем единицу. Обратный код равен 1 011 1010.

3. Прямой код получаем из обратного заменой всех двоичных цифр числа на противоположные (1 на 0, 0 на 1). Прямой код числа равен 1 100 0101 (в знаковом разряде записываем 1).

4. Число в двоичной системе счисления получаем из записи прямого кода – -100 0101₍₂₎.

4. Число -1000101₍₂₎после перевода в десятичную систему счисления равно -69₍₁₀₎.