Точечной называют оценку, которая определяется одним числом.
Интервальной называют оценку, которая определяется началом и концом некоторого интервала.
Примеры:
- по данным испытаний металла на растяжение предел текучести равен 330 МПа – точечная оценка;
- отклонения геометрических размеров сечения тоннеля от проектных лежат в интервале 0…5 см – интервальная оценка.
Надежностью (доверительной вероятностью) оценки параметра qпо его статистической характеристике q* называют вероятность g, с которой осуществляется неравенство 
, где 
характеризует точность оценки:
. (5.8)
Обычно надежность оценки задана. Наиболее часто g принимают близкой к 1.
Пример. Нормативную прочность бетона оценивают с надежностью 0,95, расчетное сопротивление – с надежностью 0,9986.
Из формулы (5.8) вытекает понятие доверительного интервала, т.е. интервала, который покрывает неизвестный параметр q с заданной надежностью g:
(5.9)
Построение доверительных интервалов для оценки математического ожидания нормального распределения при известной дисперсии
Пусть случайная величина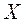 
имеет нормальное распределение: 
.
Известно значение 
и задана доверительная вероятность (надежность) 
. Требуется построить доверительный интервал для параметра 
по выборочному среднему 
.
Чтобы подчеркнуть случайный характер обозначим его 
.
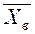Примем без доказательства, что если случайная величина 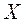распределена нормально, то и выборочное среднее 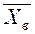, найденное по независимым наблюдениям, также распределено нормально.
Параметры распределения 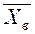таковы: 
; 
.
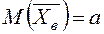Из теории вероятности известна формула для нормально распределенной случайной величины :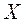
,
где 
- функция Лапласа, значение которой в точке 
находим по таблице (Приложение 2).
Учитывая, что 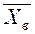имеет нормальное распределение можно записать
или 
,
где 
Из последнего равенства по таблице Лапласа находим 
(Приложение 2).
Тогда 
и доверительный интервал
покрывает с надежностью математическое ожидание .
Пример 6. Случайная величина имеет нормальное распределение с известным средним квадратическим отклонением 
. Найти доверительный интервал оценки неизвестного математического ожидания по выборочной средней , если объем выборки 
, а надежность оценки 
.
¦ 1. Находим : 
По таблице значений функции Лапласа 
.
2. Определяем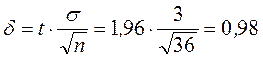 
.
Доверительный интервал запишется в виде: 
. ?
Построение доверительных интервалов для оценки математического ожидания нормального распределения при неизвестной дисперсии
