В качестве критериев оценки назависимости могут применяться и другие коэффициенты корреляции, например показатель ранговой корреляции Спирмена, позволяющий оценить нелинейную, но монотонную зависимость: в этом случае вычисляется кореляция не самих значений, а их рангов (порядковых номеров при упорядочении). Другим ранговым критерием является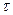 
-критерий Кендалла.
Проверка по нескольким критериям может быть использована для приблизительной оценки оценки вида зависимости: если ранговая корреляция большая (статистически значимая), а линейная – маленькая (статистически не значимая), то зависимость нелинейная; если обе корреляции большие, то зависимость линейная; если обе корреляции маленькие, что либо зависимости нет, либо она немонотонная.
Если основная гипотеза гласит, что коэфициент корреляции равен не нулю, а некоторому отличному от нуля числу, то в качестве критериальной статистики используется z -преобразование Фишера:
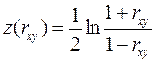
Эта величина распределена примерно нормально для всех значений коэффициента корреляции генеральных совокупностей, ее матожидание равно 
, а дисперсия 
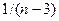, где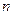 
- объем выборки. Поэтому границы доверительного интервала для находят с использованием квантилей нормального распределения; получить границы для 
можно обратным преобразованием.
Описание функции
cor.test(x, y,alternative = c("two.sided", "less", "greater"), method = c("pearson", "kendall", "spearman"), conf.level = 0.95,...)
Параметры
| x, y | Числовые вектора х и у одинаковой длины. |
| alternative | Выбирает альтернативную гипотезу одну из "two.sided" (по умолчанию)-двустороняя критическая область, "greater" -правостороняя критическая область или "less"-левостороняя критическая область. |
| method | Выбирает какой коэфициент корреляции используется в тесте. Один из"pearson", "kendall", или "spearman". |
| conf.level | Доверительная вероятность |
Примечание
Для проверки нулевой гипотезы H0 о равенстве показателя корреляции нулю необходимо в alternative выбрать "two.sided".
Критическое значение находят по таблице критических точек распределения Стьюдента с числом степей свободы 
(в R используется функция вычисления квантилей распределения Стьюдента qt(p,df)).
Пример
> x<-c(3.6,7.8,9.6,5.7,8.9)
> y<-c(2.7,8.9,6.5,8.8,6.4)
> cor.test(x,y,alternative = c("two.sided"), method = c("pearson"))
Pearson's product-moment correlation
t = 0.9142, df = 3, p-value = 0.428
95 percent confidence interval: -0.7063858 0.9555364
sample estimates: cor = 0.4667999
> cor.test(x,y,alternative= c("two.sided"), method=c("spearman"))
Spearman's rank correlation rho
S = 16, p-value = 0.7833
sample estimates: rho = 0.2
Значение
Для обычной линейной корреляции (Пирсона) мы получили выборочное значений 0.4668, значение t - статистики 0.9142 при 3 степенях свободы, и p -value равное 0.428. Это означает, что отвергнуть нулевую гипотезу можно только при допущении ошибки в 42.8%. 95% доверительный интервал равен (-0.7063858, 0.9555364) и поскольку он содержит ноль, то нулевая гипотеза принимается на 5% уровне значимости.
Для ранговой корреляции Спирмена выборочное значений коэффициента корреляции еще меньше (0.2), а p -value еще больше (0.7833). Поэтому и по ранговому критерию мы отвергаем наличие связи между X и Y.
Линейная регрессия
Описание
Линейная зависимость между переменными описывается уравнением общего вида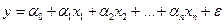 
где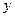 
- зависимая переменная, 
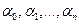- неизвестные константы, 
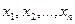- известные (независимые) переменные, и 
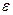- нормально распределенная случайная величина с нулевым матожиданием и дисперсией 
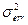. Задачей построения линейной среднеквадратической модели регрессионной зависимости переменной 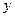от независимых переменных является получение оценки параметров 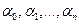и оценка адекватности построенной модели вида
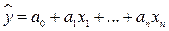
где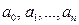 
- оценки параметров 
.
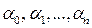Рассмотрим простейший случай одной независимой переменной:
В этом уравнении модели линейной регрессии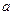 
- свободный член, а параметр 
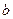определяет наклон линии регрессии по отношению к осями координат. Параметры 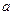и 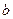определяются методом наименьших квадратов, который приводит к формуле:
,
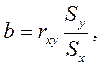
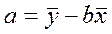где
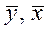- выборочные средние арифметические;
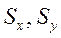- выборочные средние квадратичые отклонения;
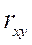- выборочный коэффициент корреляции.
Для построения линейной модели регрессии используется функция lm(formula=f), которая в простейшем случае содержит только формулу от переменных (векторов, содержащих элементы парной выборки); запись y~x означает, что строится модель зависимости y от x.
> x<-c(3.6,7.8,9.6,5.7,8.9)
> y<-c(2.7,8.9,6.5,8.8,6.4)
> p.lm<-lm(formula=x~y)
> summary(p.lm)
Residuals:
1 2 3 4 5
-1.7151 -0.3409 2.5529 -2.3954 1.8985
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.0845 3.5050 1.165 0.328
y 0.4558 0.4985 0.914 0.428
Residual standard error: 2.511 on 3 degrees of freedom
Multiple R-Squared: 0.2179, Adjusted R-squared: -0.0428
F-statistic: 0.8358 on 1 and 3 DF, p-value: 0.428
Команда summary() выдает полную информацию о построенной модели:
значения остатков (residuals - разность модельных и истинных значений переменной y). Если объем выборки большой, то печатается оценка распределения остатков (квартили).
коэфициенты модели и оценку их значимости по критерию Стьюдента (в нашем случае все коэфициенты не значимы, поскольку все вероятности (0.328 и 0.428) больше 0.05 - т.е. нельзя считать, что существует линейная зависимость между x и y).
Оценку значимости зависимости по критерию Фишера и квадрат коэфициента корреляции (R-squared), который показывает долю дисперсии y, объясненной с использованием модели (исправленное значение для R2 равно 0, статистика Фишера F =0.8358, уровень значимости критерия Фишера 42.8%, т.е. зависимость отсуствует).
Для визуализации построенной модели можно использовать вспомогательные функции:
Описание функций
abline(a, b, untf = FALSE,...)
abline(h=, untf = FALSE,...)
abline(v=, untf = FALSE,...)
Параметры
| a,b | Параметры в линейном уравнении |
| untf | Если TRUE, то рисует линию в преобразованных координатах |
| h,v | Y и Х значения для горизонтальной и вертикальной линии соответственно |
plot(x, y, xlim=range(x),ylim=range(y),type="p", main, xlab, ylab,...)
Параметры
| X,Y | Координаты точек x и y. |
| xlim, ylim | Значения для осей x и y. |
| Type | Тип графика(“ p” для точек) |
| Main | Название графика |
| Xlab,ylab | Название осей. |
Функция abline()строит прямую по найденным a и b.
Функция plot() строит экспериментальные точки.
Пример
plot(x,y)
abline(lm(x~y))
|
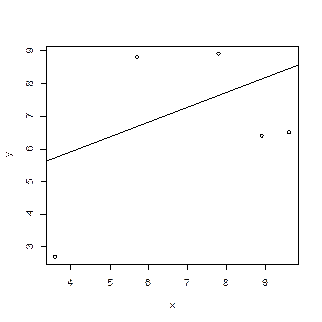
Список литературы.
1. Гмурман В.Е. Теория вероятностей и математическая статистика/ В.Е.Гмурман.М.:Высшая школа, 2000.-479с.
2. Лакин Г.Ф. Биометрия/ Г.Ф. Лакин. М: Высшая школа, 1990.-352с.
3. Теория вероятностей и математическая статистика/ Под редакцией В.А. Колемаева. М: Высшая школа, 1991.-400с.
4. Гайдышев И. Анализ и обработка данных: специальный справочник -СПб: Питер, 2001.-752с.
5. Бейли Н. Статистические методы в биологии/Н.Бейли.М.:Мир,1963.-272с.
6. Гланц С. Медико-биологическая статистика/ С. Гланц. М: Практика, 1999.-449с.
7. А.А.Савельев, С.С.Мухарамова, А.Г.Пилюгин, Е.А.Алексеева Основные понятия языка R / А.А.Савельев, С.С.Мухарамова, А.Г.Пилюгин, Е.А.Алексеева К ффф 2007.-28с
