КазанСКИЙ ГОСУДАРСТВЕННЫЙ архитектурНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Кафедра сопротивлениЯ материалов
И основ теории упругости
по выполнению контрольных работ по курсу «Сопротивление материалов» для студентов заочной формы обучения специальностей 290300, 290600, 290700, 290800, 291000, 291100, 291500, 060800,
Раздел I
Казань, 2007
Составители: к.ф.-м.н., доцент Низамеев В.Г., к.т.н., доцент Ольховик Л.С., к.ф.-м.н., доцент Богданович А.У.
Под редакцией к.т.н., доцента Л.С.Ольховик
УДК 539.3
ББК 22.251
Методические указания по выполнению контрольных работ по курсу «Сопротивление материалов» для студентов заочной формы обучения / Каз.гос. арх.-строит. университет; Состав.: Низамеев В.Г., Ольховик Л.С., Богданович А.У. Казань, 2007. 34 с.
В методических указаниях изложены: исходные данные, расчетные схемы, постановка задач, перечень этапов работы и примеры их выполнения.
Рецензенты:
Д.ф.-м.н., профессор Р.А.Каюмов
ÓКазанский государственный архитектурно-строительный университет, 2007.
Порядок выполнения
Контрольных работ по сопротивлению материалов
Контрольные работы №1, №2выполняются в 5-ом семестре; работы №3, №4 - в 6-ом семестре; работа №5 - в 7-ом семестре.
Контрольные работы состоят из следующих задач:
Работа №1 задачи 1.1-1.3; Работа №2 задачи 2.1-2.3;
Работа №3 задачи 3.1-3.2; Работа №4 задачи 4.1-4.3;
Работа №5 задачи 5.1-5.2.
Исходные данные для каждой задачи (значения действующих сил, геометрические размеры и т.д.) выбираются из таблиц согласно шифра.
Все столбцы таблиц обозначены внизу начальными буквами русского алфавита (а,б,в,г,д,е). Из каждого столбца берется то значение, которое соответствует данной букве по шифру.
ШИФР - шестизначное число образуется из первых трех букв фамилии студента и последних трех цифр зачетки. Буквенную часть шифра преобразуют в цифровую согласно таблицы.
Шифр один для всех работ. Указывается на титульном листе каждой работы. Работа без шифра не рассматривается!
| А | Й | У | Э | Пример студент Ибрагимов зачетка 11-01-105 ИБР 028 Шифр 028105 | |
| Б | К | Ф | Ю | ||
| В | Л | Х | Я | ||
| Г | М | Ц | |||
| Д | Н | Ч | |||
| Е | О | Ш | |||
| Е | П | Щ | |||
| Ж | Р | Ъ | |||
| З | С | Ы | |||
| И | Т | Ь |
Каждой цифре шифра ставится в соответствие буква русского алфавита.
0 2 8 1 0 5
А б в г д е
В таблицах, приведенных для каждой работы, из столбца а необходимо взять число, стоящее в десятой строке (0), из столбца б - число, стоящее во второй строке (2), из столбца в - число, стоящее в восьмой строке (8) и т.д.
Работы оформляются в отдельной тетради с полями для замечаний рецензента. Обязательно условие задачи с числовыми данными и расчетной схемой. Решение задачи должно сопровождаться краткими пояснениями. В окончательных результатах необходимо указывать единицы измерения всех величин. Вычисления вести в системе СИ.
ЗАДАЧИ ДлЯ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА №1
ЗАДАЧА 1.1 Стальная колонна (Е = 2×104 кН/см2 ) находится под действием продольной силы Р и собственного веса(g = 78 кН/м3). Требуется: 1) построить эпюры усилий и напряжений; 2) определить опасное сечение и проверить прочность колонны при [s]=16 кН/см2 (вопросы устойчивости не рассматриваются); 3) определить перемещение верхнего среза колонны (собственный вес колонны не учитывать). Данные взять из табл. 1 согласно рис.1.1.
ЗАДАЧА 1.2. Абсолютно жесткий брус опирается на шарнирно неподвижную опору и прикреплен к двум стальным стержням при помощи шарниров (рис. 1.2). Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу Q; 2) из условия прочности найти допускаемую нагрузку [Q] ([s]=16 кН/см2); 3) Найти предельную грузоподъемность системы QТ и допускаемую нагрузку [Q]Т, если предел текучести sТ= 24 кН/см2 и запас прочности к = 1,5; 4) сравнить величины [Q] и [Q]Т, полученные при расчете по допускаемым напряжениям (п. 2) и допускаемым нагрузкам (п. 3). Данные взять из табл.1.
ЗАДАЧА 1.3. К стальному валу приложены четыре момента (рис. 1.3). Требуется: 1) построить эпюру крутящих моментов; 2)при заданном значении[t] определить диаметр вала из расчета на прочность и округлить его значение до ближайшего, равного: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100 мм; 3) построить эпюру углов закручивания (G = 8×103 кН/см2); 4) найти наибольший относительный угол закручивания (на 1 м длины вала). Данные взять из таблицы 1.
Таблица 1
| Номер строки | Схема по рис. 1.1, 1.2, 1.3 | A, см2 | a, м | b, м | c, м | P, кН | Моменты в кНм | кНм М4 | [t], МПа | ||
| М1 | М2 | М3 | |||||||||
 1
| I | 2,1 | 2,1 | 1,1 | 1,0 | 0,5 | 5,5 | 5,0 | |||
| II | 2,2 | 2,2 | 1,2 | 1,5 | 1,0 | 5,0 | 4,5 | ||||
| III | 2,3 | 2,3 | 1,3 | 2,0 | 1,5 | 4,5 | 4,0 | ||||
| IV | 2,4 | 2,4 | 1,4 | 2,5 | 2,0 | 4,0 | 3,5 | ||||
| V | 2,5 | 2,5 | 1,5 | 3,0 | 2,5 | 3,5 | 3,0 | ||||
| VI | 2,6 | 2,6 | 1,6 | 3,5 | 3,0 | 3,0 | 2,5 | ||||
| VII | 2,7 | 2,7 | 1,7 | 4,0 | 3,5 | 2,5 | 2,0 | ||||
| VIII | 2,8 | 2,8 | 1,8 | 4,5 | 4,0 | 2,0 | 1,5 | ||||
| IX | 2,9 | 2,9 | 1,9 | 5,0 | 4,5 | 1,5 | 1,0 | ||||
| X | 3,0 | 3,0 | 2,0 | 5,5 | 5,0 | 1,0 | 0,5 | ||||
| е | д | г | в | б | а | е | д | г | в | б |
P
A A 2A A 2A
P P
A 2A
P P
A 2A A A A
I II III IV V
P
A A 2A A 2A
P P P
P
 |
A 2A A 2A A
VI VII VIII IX X
Рис.1.1
I II III
2A 2A A 
A A 2A 
C a b a c b a c b
IV V
A 2A
 |  | ||
2A A
 |
a c b c a b
VI VII VIII
 | |||||
 |  |
2A A A 2A A2A
 | |||
 |
 | |||
 | |||
c b a a b c a b c
IX X
 |  | ||
2A A A 2A
 |  |  | |||||
 | |||||||
 | |||
 | |||
c b a c c a b c
Рис.1.2
M1 M2 M3 M4
I
M1 M2 M3 M4
II
 |  |  | |
M1 M2 M3 M4
III
 |  |  | |
M1 M2 M3 M4
IV
 |  | |  | ||||
M1 M2 M3 M4
V
 |  |  | | ||||
M1 M2 M3 M4
VI
 | |||||||
 |  | |
M1 M2 M3 M4
VII
M1 M2 M3 M4 
VIII
M1 M2 M3 M4 
IX
M1 M2 M3 M4 
X
a b c a
Рис.1.3
КОНТРОЛЬНАЯ РАБОТА №2
ЗАДАЧА 2.1 Для заданного поперечного сечения (рис. 2.1, табл.2) требуется: 1) определить положение главных центральных осей инерции и вычислить соответствующие осевые моменты инерции; 2) построить эллипс инерции и определить направления наибольшей и наименьшей жесткости на изгиб.
При расчетах использовать таблицы сортамента (части стандартных профилей прямоугольниками не заменять). Сечение и эллипс вычертить в масштабе 1:2. Указать начальные, промежуточные и главные центральные оси.
ЗАДАЧА 2.2 Для заданной схемы балки (рис.2.2) требуется: написать выражения перерезывающих сил Qy и изгибающих моментов Mx для каждого участка в общем виде, построить их эпюры, установить расчетные значения внутренних силовых факторов (Qymax, Mxmax) и подобрать деревянную балку при [s] = 0,8 кН/см2, [t] = 0,4 кН/см2: а) круглого поперечного сечения; б) прямоугольного поперечного сечения при заданном соотношении h/b= 2. Данные взять из табл.2
ЗАДАЧА 2.3 Для заданной схемы балки (рис. 2.3) требуется: 1) написать выражения перерезывающих сил Qy и изгибающих моментов Mx для каждого участка в общем виде, построить их эпюры, установить расчетные значения внутренних силовых факторов (Qymax, Mxmax) и подобрать стальную балку стандартного двутаврового профиля при [s]=16 кН/см2, [t]=8 кН/см2; 2) записать дифференциальные уравнения изогнутой оси балки для всех ее участков, выполнить интегрирование и построить эпюры углов поворота сечений и прогибов балки; 3) Проверить балку на жесткость по максимальному прогибу при[ f ]= l /150, Е=2×104кН/см2, где l длина балки. Данные взять из таблицы 2.
Таблица 2
| Номер строки | Схема по рис. 2.1, 2.2, 2.3 | q кН/м | Р кН | М кНм | a м | b м | c м | l м | a | швеллер № | двутавр № | уголок № |
| 1
| I | 1,0 | 2,0 | 0,6 | 0,2 | 75х75х5 | ||||||
| II | 1,2 | 1,8 | 0,8 | 0,3 | 75х75х8 | |||||||
| III | 1,4 | 1,6 | 1,0 | 0,4 | 80х80х6 | |||||||
| IV | 1,6 | 1,4 | 1,2 | 0,5 | 80х80х8 | |||||||
| V | 1,8 | 1,2 | 1,4 | 0,6 | 90х90х7 | |||||||
| VI | 2,0 | 1,0 | 1,6 | 0,6 | 90х90х9 | |||||||
| VII | 2,2 | 0,8 | 1,8 | 0,5 | 100х100х8 | |||||||
| VIII | 2,4 | 0,6 | 2,0 | 0,4 | 24а | 100х100х10 | ||||||
| IX | 2,6 | 2,0 | 0,6 | 0,3 | 27а | 125х125х9 | ||||||
| X | 2,8 | 1,8 | 0,8 | 0,2 | 125х125х12 | |||||||
|
| е | д | г | в | б | а | е | д | г | в | б | а |
 | |||||||||
 | |||||||||
 |  | ||||||||
 | |||||||||
I II III IV V
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
VI VII VIII IX X
Рис. 2.1
M P q P q
 |  | ||||||
 | |||||||
 | |||||||
I II
P q M q M
 |
III IV
 | |||
 | |||
M P q P q
 | |||
 | |||
V VI
| |||
| |||
q P M P q M
 |  | ||
VII VIII
q M M q
 | |||
 |
P P
IX X
a b c a b c
 |  |
Рис. 2.2
q q M
 |
P
I II
M q q
 | |||
 | |||
P
III IV
Q M q
 | |||
 | |||
P
V VI
M q q
 | |||
 | |||
P
VII VIII
 |
P q M q
 | |||
 | |||
IX X
a l a l
l l
Рис. 2.3
ПРИМЕРЫ ВЫПОЛНЕНИЯ КОНТРОЛЬНЫХ РАБОТ
КОНТРОЛЬНАЯ РАБОТА № 1
ПРИМЕР К ЗАДАЧЕ 1.1
Стальная колонна (Е = 2×104 кН/см2) находится под действием продольной силы Р = 20 кН и собственного веса (g = 78 кН/м3).
Требуется:
1. Построить эпюры продольных усилий и нормальных напряжений.
2. Определить опасное сечение и проверить прочность колонны при [ s ] = 16 кН/ см2.
3. Определить перемещение верхнего среза колонны без учета собственного веса.
 
Рис.1
| Исходные данные: А =10 см2 ; a =2 м; b =1м; с =3м; Р =20 кН. |
РЕШЕНИЕ
Расчетная схема колонны (Рис.2) - ступенчатый брус, загруженный заданной сосредоточенной силой Р и распределенной нагрузкой q1, q2, q3 от собственного веса, где
q1 = g А1 = g 2А = 78×20×10-4 = 0.156 кН/м;
q2 = g А2 = g А =78×10×10-4 = 0.078 кН/м;
q3 = g А3 = g 2А =78×20×10-4 = 0.156 кН/м.
R - опорная реакция.
N, кн s, кн/см2
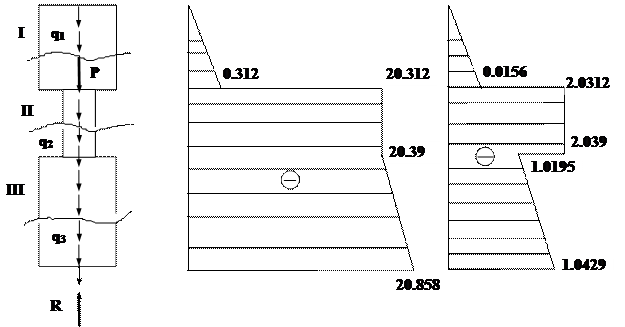Рис. 2
Разбиваем стержень на участки, начиная с верхнего свободного конца. Границами участков служат сечения в которых приложены внешние силы или же изменяется площадь поперечного сечения. В данном случае имеем три участка, площади поперечного сечения которых: А1 =2 А =20 см2, А 2= А =10см2, А 3=2 А =20см2. Ось z направляем вдоль оси стержня от верхнего среза колонны. Для каждого участка находим внутренние продольные силы NZ методом сечений из условия равновесия отсеченной верхней части (при этом отпадает необходимость в определении реакции заделки R). Нормальные напряжения sz. =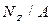 
1-ый участок 0 £ z1 £ a
0 £ z1 £ 2
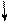
q1 z1 
Nz1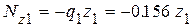 
z 
2 -ой участок a £ z 2 £ a+b
2 £ z2 £ 3
a q1 z2 
P
