Результаты проведенных измерений позволяют определить потери напора на участке трубы Т и коэффициент гидравлического трения при различных скоростях течения жидкости. Расчеты проводятся для каждого режима и их результаты заносятся в таблицу 5.3.
1. Потери напора на участие трубы Т, ограниченном точками присоединения пьезометров П1 и П2 можно определить как
,
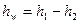где h1 и h2 - показания пьезометров П1 и П2 соответственно, м.
2. Объем жидкости, проходящей через сечение трубки Т за время Δτ, равен
W=S. Δy,
где S = 0,05 м2 – площадь зеркала воды в мерном баке;
Δy – разность уровней воды в мерном баке, м.
3. Расход воды через трубку Т.
.
4. Средняя скорость воды в трубке Т равна
,
где ω – площадь живого сечения трубки Т (d = 0,01 м), м2.
5. Число Рейнольдса
,
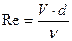где υ – коэффициент кинематической вязкости воды, зависящий от температуры. Величина υ может быть определена по эмпирической формуле Пуазейля:
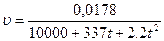, м2/с.
Для сокращения вычислений можно при определении воспользоваться таблицей:
Таблица 5.1.
| t, 0C | ||||||||||
| υ,×106, м2/с | 1,39 | 1,35 | 1,31 | 1,27 | 1,24 | 1,21 | 1,18 | 1,15 | 1,12 | 1,09 |
6. Экспериментальный коэффициент гидравлического трения может быть определен как:
,
где 
= 1 м – длина участка трубы Т между точками присоединения пьезометров П1 и П2; g - ускорение свободного падения, м/с2.
7. Расчетный коэффициент гидравлического трения определяется по эмпирическим формулам в зависимости от режима течения жидкости.
a. Re < 2320 - область ламинарного режима течения жидкости:
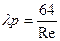
b. Re > 2320 - область турбулентного течения жидкости. При турбулентном режиме различают ряд областей, характеризующихся различными законами сопротивления: область гладкостенного течения, зоны доквадратичного и квадратичного сопротивления. Однако, для определения коэффициента гидравлического трения при турбулентном режиме движения жидкости для всех областей может быть использована обобщенная формула Альтшуля:
,
где Δ = 0,08۰10-3 м - шероховатость внутренней стенки трубы, м;
d = 0,01 м - внутренний диаметр трубы.
Форма и содержание отчета
Отчет по лабораторный работе должен содержать:
1. Задачи исследования.
2. Принципиальную схему установки с обозначениями основных элементов и их расшифровкой.
3. Результаты измерений, занесенные в таблицу 5.2.
4. Расчетные формулы с расшифровкой входящих в них величин.
5. Результаты обработки экспериментальных данных и расчетные значения, занесенные в таблицу 5.3.
6. Совмещенные графики зависимосте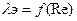й 
и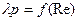 
, выполненные на миллиметровой бумаге.
Контрольные вопросы.
1. Почему потери напора в этой установке характеризуются лишь разностью пьезометрических столбов?
2. Что такое гидравлически гладкие и гидравлически шероховатые трубы? Какова с этой точки зрения труба в проведенном исследовании?
3. Как надо было бы считать hw, если бы в установке труба располагалась вертикально?
4. Что такое гидравлический уклон?
5. Можно ли считать коэффициент гидравлического трения коэффициентом трения жидкости о стенки трубы?
Приложение
Таблица 5.2.
| № п./п. | h1.102 м | h2.102 м | Δy.102 м | Δτ, с | t, 0C |
Таблица 5.3.
| № п./п | hw, м | W, м3 | V, м/с | Re | λэ | λp | 
|
Лабораторная работа № 6
