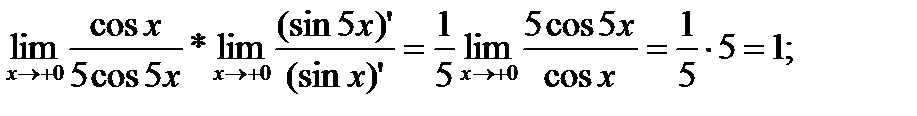Определение. Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  . Приращением этой функции в точке
. Приращением этой функции в точке  называется функция аргумента
называется функция аргумента  Производной функции
Производной функции  в точке
в точке  называется
называется  . Производная функции в точке
. Производная функции в точке  обозначается
обозначается  или
или  . Операция нахождения производной называется дифференцированием.
. Операция нахождения производной называется дифференцированием.
Таблица производных простейших элементарных функций
1.  8.
8. 
2.  9.
9. 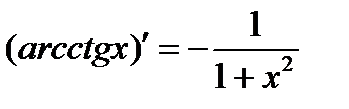
3.  10.
10. 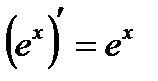
4.  11.
11. 
5.  12.
12. 
6.  13.
13. 
7. 
Физический смысл производной
Производная  - скорость изменения зависимой переменной
- скорость изменения зависимой переменной  по отношению к изменению независимой переменной
по отношению к изменению независимой переменной  в точке
в точке  . В частности, если
. В частности, если  - время,
- время,  - координата точки, движущейся по прямой, то
- координата точки, движущейся по прямой, то  - мгновенная скорость точки в момент
- мгновенная скорость точки в момент  .
.
Геометрический смысл производной
Рассмотрим график функции  .
.
y
 N
N
l
 M
M



 x
x
MN - секущая к графику функции. При  , угол
, угол 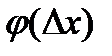 стремится к некоторому пределу
стремится к некоторому пределу  , а секущая, поворачиваясь вокруг точки M, становится касательной.
, а секущая, поворачиваясь вокруг точки M, становится касательной.

Уравнение касательной к графику функции:
 .
.
Уравнение нормали, проведённой в той же точке:
 .
.
Правила дифференцирования
Если  и
и  - дифференцируемые функции, то справедливы равенства
- дифференцируемые функции, то справедливы равенства

 ;
;
Производная сложной функции
Если функция  имеет в точке
имеет в точке  производную
производную  , а функция
, а функция  имеет в точке
имеет в точке  производную
производную  , то сложная функция
, то сложная функция  имеет производную в точке
имеет производную в точке  , причём
, причём
 . (1)
. (1)
Физическая интерпретация формулы (1): производная  - скорость изменения
- скорость изменения  по отношению к
по отношению к  , производная
, производная  - скорость изменения
- скорость изменения  по отношению к
по отношению к  . Очевидно, что скорость
. Очевидно, что скорость  равна произведению скоростей
равна произведению скоростей  и
и  . (Если
. (Если  движется быстрее
движется быстрее  в
в  раз,
раз,  - быстрее
- быстрее  в
в  раз, то
раз, то  движется быстрее
движется быстрее  в
в  раз).
раз).
Производная функции, заданной параметрически
Пусть функции  (2)
(2)
определены на некотором промежутке изменения переменной  , которую назовём параметром. Пусть функция
, которую назовём параметром. Пусть функция 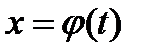 является строго монотонной на этом промежутке. Тогда существует обратная функция
является строго монотонной на этом промежутке. Тогда существует обратная функция  , подставляя которую в уравнение
, подставляя которую в уравнение  получим
получим  . Таким образом, переменная
. Таким образом, переменная  является сложной функцией переменной
является сложной функцией переменной  . Задание функции
. Задание функции  с помощью уравнений (2) называется параметрическим. Если функции
с помощью уравнений (2) называется параметрическим. Если функции  имеют производные, причём
имеют производные, причём  , то
, то  .
.
Дифференциалом функции  в точке
в точке  называется функция аргумента
называется функция аргумента  . Дифференциалом независимой переменной
. Дифференциалом независимой переменной  называется приращение этой переменной:
называется приращение этой переменной:  . Таким образом, дифференциал функции
. Таким образом, дифференциал функции  в точке
в точке  имеет вид
имеет вид
 , (3)
, (3)
откуда  .
.
Геометрический и физический смысл дифференциала
y
 N
N
 P
P
dy
 M
M 


0 
 x
x
Рассмотрим график функции  . МР- касательная к графику функции в точке М
. МР- касательная к графику функции в точке М 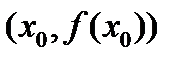 . Дифференциал
. Дифференциал  равен приращению ординаты касательной.
равен приращению ординаты касательной.
Если  - время,
- время,  - координата точки на прямой в момент
- координата точки на прямой в момент  , то дифференциал
, то дифференциал  равен тому изменению координаты, которое получила бы точка за время
равен тому изменению координаты, которое получила бы точка за время  , если бы скорость точки на отрезке
, если бы скорость точки на отрезке  была постоянной и равной
была постоянной и равной  . Изменение скорости на этом отрезке приводит к тому, что
. Изменение скорости на этом отрезке приводит к тому, что 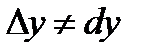 . Однако на малых промежутках времени
. Однако на малых промежутках времени  изменение скорости незначительно и
изменение скорости незначительно и  .
.
Инвариантность формы первого дифференциала
Пусть аргумент  функции
функции  является функцией от
является функцией от  , тогда дифференциал функции
, тогда дифференциал функции  по-прежнему имеет вид (3), но теперь
по-прежнему имеет вид (3), но теперь  является не произвольным приращением аргумента
является не произвольным приращением аргумента  , а дифференциалом функции
, а дифференциалом функции  , т.е.
, т.е.  . Это свойство – сохранение формы и в том случае, когда
. Это свойство – сохранение формы и в том случае, когда  называется инвариантностью формы первого дифференциала.
называется инвариантностью формы первого дифференциала.
Применение дифференциала в приближённых вычислениях
Так как  при малых
при малых  , т.е.
, т.е.  , то
, то  .
.
Эта формула позволяет находить приближённые значения  при малых
при малых  , если известны
, если известны  . При этом погрешность при такой замене при
. При этом погрешность при такой замене при 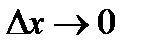 является бесконечно малой, более высокого порядка, чем
является бесконечно малой, более высокого порядка, чем  .
.
Производные высших порядков
Если производная  функции
функции  определена в некоторой окрестности точки
определена в некоторой окрестности точки  и имеет в этой точке производную, то эта производная от
и имеет в этой точке производную, то эта производная от  называется второй производной и обозначается
называется второй производной и обозначается  . Третья производная является производной от
. Третья производная является производной от  и т.д. Таким образом, производные высших порядков определяются индуктивно по формуле
и т.д. Таким образом, производные высших порядков определяются индуктивно по формуле
 .
.
Основные формулы вычисления n -х производных
1. 
2. Формула Лейбница
 , где
, где 
3. 
4. 
5. Если  , то
, то  , или
, или 
Общая схема исследования функции
и построения её графика
I. Элементарное исследование.
1. Найти область определения функции.
2. Исследовать функцию на чётность/нечётность, периодичность.
3. Вычислить предельные значения функции в граничных точках области определения.
4. Выяснить существование асимптот.
5. Определить, если это не вызовет особых затруднений, точки пересечения графика функции с координатными осями.
6. Сделать эскиз графика функции, используя полученные результаты.
II. Исследование графика функции по первой производной.
1. Найти решения уравнений 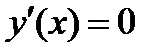 и выяснить, в каких точках производная не существует.
и выяснить, в каких точках производная не существует.
2. Точки, «подозрительные» на экстремум, исследовать с помощью достаточного условия, определить вид экстремума.
3. Найти интервалы монотонности.
III. Исследование графика функции по второй производной.
1. Найти решения уравнения  и выяснить, в каких точках производная не существует.
и выяснить, в каких точках производная не существует.
2. Точки, «подозрительные» на перегиб, исследовать с помощью достаточного условия.
3. Вычислить значения функции в точках перегиба.
4. Найти интервалы выпуклости и вогнутости.
IV. Построить график функции.
Если в некоторой окрестности точки  выполняется неравенство
выполняется неравенство 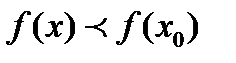 или
или  , то точка
, то точка  называется точкой экстремума функции
называется точкой экстремума функции  (соответственно точкой максимума или минимума).
(соответственно точкой максимума или минимума).
Необходимое условие экстремума: если  - точка экстремума, то
- точка экстремума, то  .
.
Достаточное условие экстремума: точка  является точкой экстремума, если её производная
является точкой экстремума, если её производная  меняет знак при переходе через точку
меняет знак при переходе через точку  , с + на – при максимуме, с – на + при минимуме.
, с + на – при максимуме, с – на + при минимуме.
Точка  называется точкой перегиба кривой
называется точкой перегиба кривой  , если при переходе через точку
, если при переходе через точку  меняется направление выпуклости.
меняется направление выпуклости.
Необходимое условие точки перегиба: если  - точка перегиба, то
- точка перегиба, то 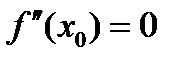 .
.
Достаточное условие точки перегиба:  является точкой перегиба кривой
является точкой перегиба кривой  , если при переходе через точку
, если при переходе через точку  вторая производная меняет знак.
вторая производная меняет знак.
Прямая  называется наклонной асимптотой кривой
называется наклонной асимптотой кривой  , если расстояние от точек кривой до асимптоты стремится к нулю при
, если расстояние от точек кривой до асимптоты стремится к нулю при  .
.
При этом
 .
.
При  имеем горизонтальную асимптоту
имеем горизонтальную асимптоту 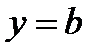 .
.
Если  или
или  , то прямая
, то прямая  называется вертикальной асимптотой.
называется вертикальной асимптотой.
Примеры
1. Пользуясь формулами дифференцирования, найти производные следующих функций:
1) 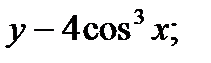 2)
2) 
3)  4)
4) 
Решение:
1)  есть сложная функция.
есть сложная функция.
 , где
, где 
Производная сложной функции имеет вид
 или
или  ,
,
следовательно,

2)  - сложная функция.
- сложная функция.
 , где
, где 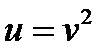 , а
, а  ,
,
 ;
;
3) применяя логарифмическое дифференцирование, последовательно находим


= 
4) 
 есть неявная функция, т.е. задана уравнением
есть неявная функция, т.е. задана уравнением  , не разрешенным относительно у. Для нахождения производной
, не разрешенным относительно у. Для нахождения производной  нужно продифференцировать по х обе части равенства, помня, что у есть функция от х, и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от х и у:
нужно продифференцировать по х обе части равенства, помня, что у есть функция от х, и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от х и у:


2. Найти производную первого и второго порядка  и
и 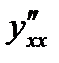 для параметрически заданной функции
для параметрически заданной функции 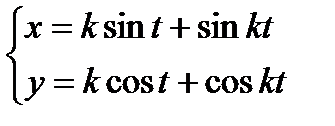 .
.
Функция у от независимой переменной х задана через посредство вспомогательной переменной (параметра t). Производная от у по х определяется формулой
 .
.
Находим производные от у и х по параметру t:


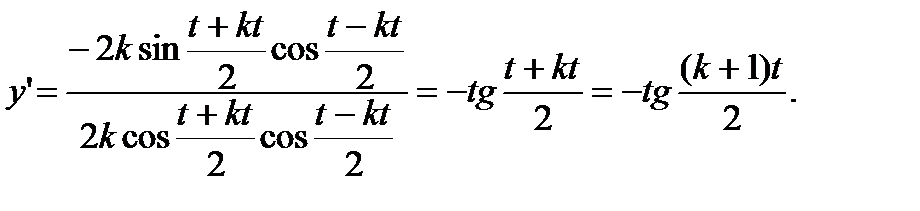
Находим производную второго порядка от y по х:
 , или
, или  .
.
Находим
 ;
;
 .
.
3. Составить уравнение касательной и нормали к кривой у = х2 - 4х в точке, где х = 1.
Решение. Уравнение касательной к кривой в точке М(х0, у0)

х0 = 1,
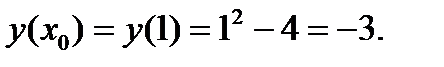
Для определения углового коэффициента касательной  находим производную
находим производную

Подставляя значения х0, у0, у'(х0) в уравнение, получим
у+3 = -2(х-1) или 2х+у+1 = 0
Уравнение нормали -

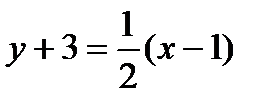 или
или  .
.
4. Найти дифференциалы функций:
1) 
 2)
2) 
вычислить  .
.
Решение. Находим производную данной функции и, умножив ее на дифференциал независимой переменной, получим искомый дифференциал данной функции:
1) 
2)  .
.
Полагая х = 0 и dx = 0,1, получим 
5. Вычислить приближенное значение:
1)  2)
2)  .
.
Решение. Если требуется вычислить  и если проще вычислить f(x0) и
и если проще вычислить f(x0) и  , то при достаточно малой по абсолютному значению разности
, то при достаточно малой по абсолютному значению разности 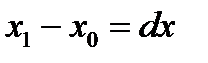 можно заменить приращение функции ее дифференциалом
можно заменить приращение функции ее дифференциалом  и тогда приближенное значение искомой величины вычисляется по формуле
и тогда приближенное значение искомой величины вычисляется по формуле

1) Будем рассматривать  как частное значение функции
как частное значение функции  при x1 =17. Пусть х0 =16, тогда
при x1 =17. Пусть х0 =16, тогда


Подставляя в формулу, получим

2) y= arctgx, x1=0,98, x0 = 1, dx=0,98-1=-0,02;

Получим
 .
.
6. Исследовать и построить график функции
 .
.
Решение:
1) заданная функция определена и непрерывна на всей числовой оси
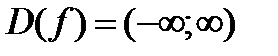 ;
;
2) функция нечетная, ибо у(-х) = -у(х), ее график будет симметричен относительно начала координат. Поэтому достаточно построить график для  ;
;
3) график функции пересекается с осями координат только в начале координат, так как у(0) = 0;
4) исследуем функцию на наличие асимптот:
а) вертикальных асимптот график функции не имеет;
б) невертикальная асимптота имеет уравнение у = kх + b.

= 

 0.
0.
Таким образом, уравнение асимптоты - у = 0;
5) исследуем функцию на экстремум:
 ;
;
у' нигде не обращается в нуль; у не существует в точках х = ±1, которые являются критическими.
Исследуем знак производной на интервале [0;∞)
0 1
х = 1 есть точка максимума,  ;
;
6) исследуем график функций на выпуклость и вогнутость:

 в точке х = 0; у " не существует в точках х = ±1. Эти точки могут быть абциссами точек перегиба.
в точке х = 0; у " не существует в точках х = ±1. Эти точки могут быть абциссами точек перегиба.
Исследуем знак второй производной на интервале [0;∞)
0 1 x
х = 1 не является точкой перегиба.
Основываясь на полученных результатах исследования, строим график функции на интервале [0;∞), затем симметрично полученному графику относительно начала координат на интервале (- ∞; 0)
Правило Лопиталя
Теорема. Пусть  и
и  дифференцируемы в некоторой окрестности точки а (за исключением, может быть, её самой), причём
дифференцируемы в некоторой окрестности точки а (за исключением, может быть, её самой), причём  . Тогда если
. Тогда если  или
или  , то
, то  при условии, что предел правой части данного равенства существует.
при условии, что предел правой части данного равенства существует.
Примеры
1. Найти пределы
1)  2)
2) 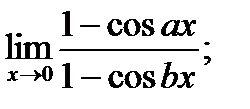
3) 
Решение. Убедившись, что имеет место неопределенность  или
или  , применяем правило Лопиталя:
, применяем правило Лопиталя:
1) 
2) 
(здесь правило Лопиталя применено дважды);
3) 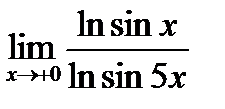 =
= 
=