Тверской государственный технический университет
Кафедра информатики и прикладной математики
ЗАДАНИЕ ПО ВЫСШЕЙ МАТЕМАТИКЕ Часть 1
Методическая разработка
для студентов заочников первого курса
Тверь 2016
УДК 517 (075.8)
ББК 22.16. я 7
Представленная методическая разработка включает основные вопросы программы по высшей математике для студентов первого курса по следующим разделам: линейная и векторная алгебра, аналитическая геометрия, пределы, непрерывность функции, дифференцирование функции.
Контрольные задания по данным разделам необходимы для приобретения практических навыков при изучении курса высшей математики.
Методические указания обсуждены и рекомендованы к печати на заседании кафедры информатики и прикладной математики (протокол №3 от 29 марта 2016 г.)
ЗАДАНИЕ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Часть1
Методическая разработка
для студентов заочников первого курса
ã Тверской государственный
технический университет, 2016
ã Романова Г.В., Стукалова Н.А., Кислова И.Л.
В методических указаниях приведены примеры и задачи по следующим разделам курса математики:
1. Линейная алгебра.
2. Векторная алгебра.
3. Аналитическая геометрия.
4. Введение в математический анализ.
5. Производная и дифференциал.
6. Исследование поведения графика функции.
Прежде чем приступить к выполнению контрольных работ, студенту необходимо изучить соответствующий теоретический материал по указанным учебникам.
Если в процессе изучения теоретического материала или при решении задач возникают вопросы, то можно обратиться к преподавателям кафедры
для получения консультации.
Во время экзаменационной сессии для студентов-заочников организуются лекции и практические занятия, которые носят обзорный характер.
При выполнения контрольной работы обратите внимание на оформление работы. НА ТИТУЛЬНОМ ЛИСТЕ ДОЛЖНЫ БЫТЬ УКАЗАНЫ:
ФАМИЛИЯ, ИМЯ, ОТЧЕСТВО
НОМЕР СТУДЕНЧЕСКОГО БИЛЕТА (или ЗАЧЁТНОЙ КНИЖКИ)
НАЗВАНИЕ ДИСЦИПЛИНЫ
НОМЕР КОНТРОЛЬНОЙ РАБОТЫ
НОМЕР ВАРИАНТА
Номер варианта, который должен выполнить студент, соответствует последней цифре номера студенческого билета (или зачетной книжки)
ТЕМА 1. ЛИНЕЙНАЯ АЛГЕБРА
Матрицы. Действия над матрицами.
Матрицей порядка 
называется прямоугольная таблица, состоящая из m - строк и n – столбцов
Часто записывают 
Если количество строк матрицы равно количеству столбцов, то матрица называется квадратной, в противном случае – прямоугольной.
Нулевой называется матрица, все элементы которой нули.
Единичной матрицей порядка n называется квадратная матрица на главной диагонали которой единицы, все остальные элементы – нули.
Диагональной называется квадратная матрица, у которой все элементы вне главной диагонали равны нулю.
Главная диагональ квадратной матрицы содержит элементы 
Побочная диагональ квадратной матрицы содержит элементы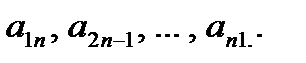 
Произведением матрицы 
на число k называют матрицу 
, в которой элементы 
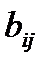определяют по правилу 
. При этом пишут 
.
Суммой матриц и называют матрицу 
, элементы которой равны сумме соответствующих элементов матриц А и В, т.е. 
При этом пишут С=А+В. Складывать можно матрицы одинаковой размерности.
Транспонирование матрицы – это перестановка строк в столбцы.
Пусть дана матрица , то 
Произведением матрицы 
на матрицу 
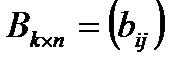называют матрицу 
, элементы которой определяются по правилу 
. При этом пишут С=АВ.
Заметим, что произведение матриц определено, если количество столбцов первого сомножителя совпадает с количеством строк второго.
Введённые операции над матрицами обладают свойствами суммы и произведения чисел:
А+В=В+А А(В+С)=АВ+АС
α(А+В)=αА+αВ А+(В+С)=(А+В)+С
(α+β)А=αА+βА А(ВС)=(АВ)С
Не выполняется лишь коммутативность умножения, т.е. АВ≠ВА.
Определители.
Каждой квадратной матрице А ставится в соответствие число, называемое определителем и обозначаемое det A или 
.
Определитель матрицы порядка 1 равен элементу матрицы.
Определитель второго порядка вычисляется по формуле
Определитель третьего порядка вычисляется по формуле
Для вычисления определителя третьего порядка лучше пользоваться правилом Саррюса (треугольников) или правилом «3 
5»
Правило Саррюса состоит в том, что девять чисел, составляющих определитель, разбиваются на 6 троек. Тройке придаётся знак «+», если элементы, входящие в неё, расположены на главной диагонали или в вершинах треугольника с основанием параллельным главной диагонали, или знак «-», если элементы, входящие в тройку, расположены на побочной диагонали или в вершинах треугольника с основанием параллельным побочной диагонали. Затем берётся сумма произведений элементов троек с учётом их знаков.
Правило «
» использует схему
(к матрице добавлены первые два столбца)
Элементы матрицы соединены отрезками. Произведению элементов, составляющих тройку и лежащих на одном отрезке, придаётся знак «+», если отрезок параллелен главной диагонали, и «-», если побочной. Определитель равен сумме произведений элементов троек с учётом их знаков.
Определитель треугольной и диагональной матрицы равен произведению элементов главной диагонали. Для вычисления определителя иногда оказывается удобным приведение матрицы к треугольному виду с использованием свойств определителя.
Матрица, определитель которой равен нулю, называется вырожденной.
Свойства определителя
1). det A=detA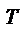 
2). При перестановке двух строк меняется знак определителя.
3). Определитель матрицы, имеющей нулевую строку, равен нулю.
4). Определитель матрицы, имеющей две одинаковые строки, равен нулю.
5). Общий множитель строки можно вынести за знак определителя.
6). Если к элементам одной строки прибавить элементы другой строки, умноженные на одно и то же число, то определитель не изменится.
7). Все свойства, перечисленные для строк, верны и для столбцов.
8). det(AB)=detAdetB.
Минором элемента 
называется определитель 
, полученный из матрицы А после вычёркивания i – й строки и j – го столбца.
Алгебраическим дополнением элемента называется число 
.
Любой определитель можно разложить по любой строке или столбцу
det 
det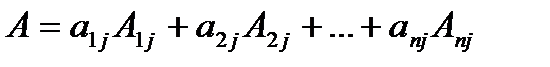 
Обратная матрица
Матрица 
называется обратной к матрице A, если 
.
Матрица имеет обратную только в том случае, если она невырожденная.
Обратная матрица находится по правилу
где 
- алгебраические дополнения элементов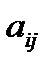 
. Можно применить элементарные преобразования для нахождения обратной матрицы. Выпишем матрицу А и справа припишем единичную матрицу того же порядка и над строками их будем одновременно производить элементарные преобразования до тех пор, пока матрица А не превратиться в единичную. Тогда единичная матрица превратится в обратную.
Можно единичную матрицу располагать над матрицей А и производить элементарные преобразования над столбцами, тогда исходная единичная матрица превратится в обратную.
Ранг матрицы
Выберем в матрице 
k – строк и k – столбцов 
. Из элементов, стоящих на пересечении выделенных строк и столбцов составим определитель k – го порядка, который назовём минором k – го порядка матрицы А. Рангом матрицы А называется число r, удовлетворяющее следующим условиям: 1) существует по крайней мере один минор порядка r, отличный от нуля; 2) все миноры порядка (r+1) равны нулю.
При этом пишут rank A=r. Если ранг матрицы А равен r, то любой отличный от нуля минор порядка r называется базисным.
Итак, для того чтобы вычислить ранг матрицы, необходимо вычислить все её миноры и среди них найти минор наибольшего порядка 
.
Очевидно, что ранг невырожденной матрицы равен порядку матрицы.
Не изменяют ранг матрицы следующие элементарные преобразования:
1) перестановка строк или столбцов;
2) умножение строк (столбцов) на число ;
3) прибавление к любой строке (столбцу) другой строки (столбца), умноженной на число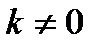 
;
4) зачёркивание нулевой строки (столбца);
5) транспонирование.
Трапецеидальной матрицей называется матрица, имеющая вид
где 
Другими словами, матрица 
является трапецеидальной, если 
при 
и 
.
Ранг такой матрицы равен m.
Таким образом, для нахождения ранга матрицы с помощью элементарных преобразований нужно привести матрицу к трапецеидальному виду.
