2.1 Уравнение вида
 (1)
(1)
Легко решается в квадратурах путем п кратного интегрирования:
 .
.
Часто произвольные постоянные не выписываются в явном виде, а подразумеваются включенными в интегралы.
2.2 Уравнение вида
 (2)
(2)
которое не разрешимо в элементарных функциях относительно производной следует заменить двумя параметрическими уравнениями:

эквивалентными уравнению (2).
По определению,  , или, в нашем случае,
, или, в нашем случае,  откуда
откуда
 ;
;
далее,
 и т.д.
и т.д.
(Мы не пишем произвольных постоянных, включая их в знак неопределенного интеграла; если написать их явно, то, например, в выражении для 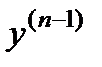 появится член С1, в выражении для
появится член С1, в выражении для  члены С2 и С1 х или
члены С2 и С1 х или  и т.д.)
и т.д.)
В результате получим:

Если из этих двух соотношений исключить t, получим общий интеграл уравнения (2).
П р и м е р 1. 
Здесь разрешение относительно  в элементарных функциях невозможно. За параметр t удобно взять
в элементарных функциях невозможно. За параметр t удобно взять  , и мы получаем параметрические уравнения:
, и мы получаем параметрические уравнения:  = t,
= t,  . Отсюда
. Отсюда


далее,
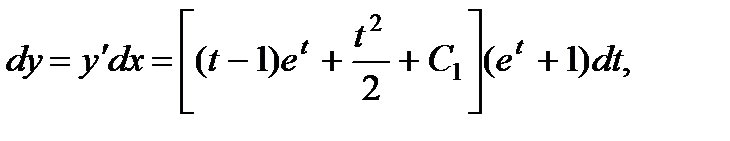

или
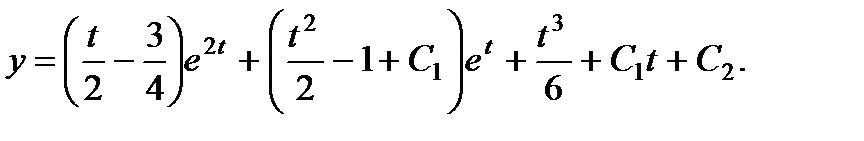
Последняя формула вместе с выражением для х: 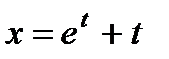 дает параметрическое представление общего решения данного уравнения.
дает параметрическое представление общего решения данного уравнения.
2.3 Уравнение вида
 (3)
(3)
введением новой функции z:  приводится к уравнению первого порядка
приводится к уравнению первого порядка  , которое легко интегрируется методом разделения переменных:
, которое легко интегрируется методом разделения переменных:

Допустим, что это соотношение разрешено относительно z:
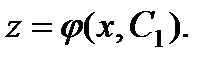
Заменяя z его значением  , получим уравнение (п – 1)-го порядка:
, получим уравнение (п – 1)-го порядка:

Которое рассмотрено в разд. 2.1; при его интеграции войдут еще п – 1 произвольных постоянных, и мы получим общее решение уравнения (3) в виде:
 .
.
2.4 Уравнение вида
 (4)
(4)
приводится к квадратурам при любом натуральном п. Если оно легко разрешимо относительно старшей производной, то приходим к рассмотренному выше типу 2.3.
В противном случае уравнение (4) заменяем двумя параметрическими уравнениями

Тогда соотношение  или
или 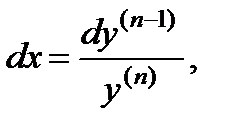 дает нам
дает нам 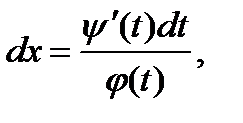 откуда х получается квадратурой:
откуда х получается квадратурой:

Далее находим последовательно:




и, наконец,

Т.е. опять представление у и х в функции параметра t и п произвольных постоянных 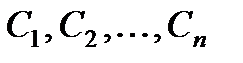 , следовательно, общее решение.
, следовательно, общее решение.
П р и м е р 2. 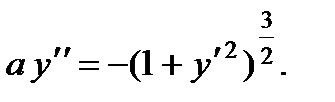
Согласно изложенной теории, полагая  , получаем уравнение первого порядка:
, получаем уравнение первого порядка:
 или
или 
откуда 
Дальше удобно интегрировать в параметрическом виде:

Отсюда находим:

Исключая параметр 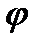 , получаем общий интеграл:
, получаем общий интеграл:

представляющий уравнение семейства всех окружностей радиуса а на плоскости х, у.
П р и м е р 3. Найти решение задачи Коши 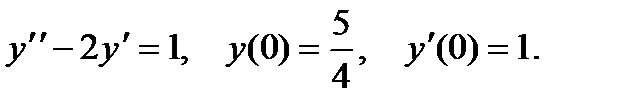
Пусть  тогда
тогда  или
или  Интегрируя полученное уравнение, находим общее решение:
Интегрируя полученное уравнение, находим общее решение:

Учитывая начальные условия, определим С1 и С2: 
Частное решение уравнения запишется в виде 
2.5 Уравнения вида
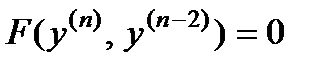 (5)
(5)
также интегрируются в квадратурах. Введение нового переменного  приводит
приводит
уравнение (5) к уравнению второго порядка:  Если это уравнение разрешено относительно
Если это уравнение разрешено относительно  , т.е. имеет вид:
, т.е. имеет вид:  то один из методов его интеграции таков: умножив обе части на
то один из методов его интеграции таков: умножив обе части на 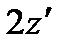 , получаем:
, получаем:  или в дифференциалах:
или в дифференциалах:

откуда

Последнее уравнение можно разрешить относительно производной и разделить переменные:

отсюда находим общий интеграл уравнения  :
:

Этот интеграл при замене z на  принимает вид:
принимает вид:

т.е. уравнение вида (2); оно интегрируется, как мы уже знаем, квадратурами, причем эта интеграция дает еще п – 2 произвольных постоянных. И мы получим общее решение уравнения (5).
П р и м е р 4. 
Полагая  приходим к уравнению:
приходим к уравнению:  ; умножим обе части на
; умножим обе части на  :
:
 или
или 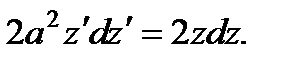
интегрируя, находим:
 ,
,
откуда

Вторая интеграция дает:
 или
или 
Чтобы решить последнее уравнение относительно z, выгодно поступить следующим образом: делим 1 на обе части последнего равенства:

в левой части освобождаемся от иррациональности в знаменателе, затем умножаем обе части на (- С1) и получаем:

Складывая это уравнение с исходным и деля на 2, получаем:

Подставляя вместо z его значение 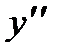 и интегрируя два раза, находим:
и интегрируя два раза, находим:

где А, В, С, D – произвольные постоянные.
2.6 Уравнение типа  в параметрическом виде
в параметрическом виде
Если уравнение (5) дано в не разрешенном относительно 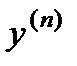 виде, но известно
виде, но известно
его параметрическое представление

то интеграция совершается следующим образом. Мы имеем два равенства:

связывающих две неизвестные функции от t, именно х и у; исключая делением на dx, получаем дифференциальное уравнение для  :
:

или, в силу параметрического представления, получим

откуда квадратурой находим  далее получим:
далее получим:
 .
.
Имея параметрическое представление  и
и  , мы свели задачу к типу 2.4. Дальнейшие квадратуры дадут п – 1 новых производных постоянных.
, мы свели задачу к типу 2.4. Дальнейшие квадратуры дадут п – 1 новых производных постоянных.






