ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
ПОРЯДКА ВЫШЕ ПЕРВОГО
Методические указания и индивидуальные задания
Самара 2010
Составитель: И.В. Алименков
УДК 517.912
Обыкновенные дифференциальные уравнения порядка выше первого: Метод.
Указания/ Самара.гос.аэрокосм.ун-т.
Сост. И.В. Алименков. Самара, 2010. 36 с.
В сжатой форме приведены основные понятия теории обыкновенных дифференциальных уравнений порядка выше первого. Сформулированы основные теоремы и описаны аналитические методы решения уравнений п -го порядка. Особое внимание уделено типам уравнений, разрешимых в квадратурах. Изложение сопровождается подробными решениями типовых примеров. Представлено 25 вариантов индивидуальных заданий, каждый из которых содержит 8 задач.
Печатается по решению редакционно-издательского совета Самарского государственного аэрокосмического университета имени академика С.П.Королева.
Рецензент А.А.Дегтярев.
Содержание
Предисловие …………………………………………………………………………………… 4
1 Общие понятия и определения. Теорема существования и единственности ………… 5
1.1 Уравнения п-го порядка …………………………………………………………………. 5
1.2 Теорема существования и единственности ………………………………….………… 5
2 Типы уравнений высших порядков, решаемые в квадратурах ………………………… 6
2.1 Уравнение вида 
……………………………………………………………… 6
2.2 Уравнение вида 
…………………………………………………………… 6
2.3 Уравнение вида 
…………………………………………………………. 7
2.4 Уравнение вида 
………………………………………………………. 7
2.5 Уравнение вида 
……………………………………………………… 9
2.6 Уравнение типа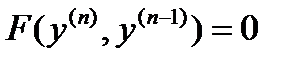 
в параметрическом виде …………………………. 10
3 Уравнения, допускающие понижение порядка ………………………………………... 10
3.1 Уравнения, не содержащие явно искомой функции ………………………………….. 10
3.2 Уравнения, не содержащие явно независимого переменного ……………………….. 11
3.3 Понижение порядка в однородных уравнениях различных типов ………………….. 12
3.4 Уравнения, левая часть которых является точной производной …………………….. 15
4 Линейные дифференциальные уравнения произвольного порядка ………………….. 16
4.1 Линейное однородное дифференциальное уравнение ……………………………….. 16
4.2 Линейное неоднородное дифференциальное уравнение …………………………….. 20
4.3 Линейные уравнения с постоянными коэффициентами …………………………….. 21
4.3.1 Линейные однородные уравнения ……………………………………………… 21
4.3.2 Линейные неоднородные уравнения …………………………………………… 23
Варианты индивидуальных заданий для самостоятельной работы …………………….. 25
Список литературы ………………………………………………………………………… 36
Предисловие
В данных методических указаниях рассматриваются дифференциальные уравнения порядка выше первого, интегрируемые в квадратурах. Приведены краткие сведения из теории, разработаны типовые примеры и представлены 25 вариантов индивидуальных заданий.
Предназначены для студентов направлений 010501 – «Прикладные математика и информатика», а также 019600 – «Прикладные математика и физика» в качестве руководства при подготовке к практическим занятиям и выполнению индивидуальных заданий.
Автор обращается к читателям с просьбой направлять свои отзывы о данной методической работе на кафедру прикладной математики Самарского государственного аэрокосмического университета имени академика С.П. Королева. Все критические замечания будут рассмотрены и учтены при следующих изданиях.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
1 Общие понятия и определения. Теорема существования и единственности
1.1 Уравнения п-го порядка.
Дифференциальное уравнение п-го порядка имеет вид
(1)
где х – независимая переменная, у – искомая функция. Функция F предполагается непрерывной в некоторой области G изменения своих аргументов.
В виде, разрешенном относительно старшей производной уравнение (1)
записывается как
(2)
Где функция f непрерывна в некоторой области D изменения своих аргументов.
Решением уравнения (2) называется функция у(х), заданная на интервале (а,в) и
удовлетворяющая следующим условиям:
§ у(х) непрерывно дифференцируема п раз на (а,в);
§ 
принадлежит области D при всех х из (а,в);
§ У(х) обращает уравнение (2) в тождество при всех х из (а,в).
1.2 Теорема существования и единственности
Задачей Коши для дифференциального уравнения (2) называется нахождение
решения у(х), удовлетворяющего следующим начальным условиям
(3)
где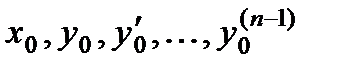 
- заданные числа.
Существование и единственность решения указанной задачи определяется
теоремой Коши:
Если функция f непрерывна в замкнутой области D, содержащей точку М 
, и имеет непрерывные частные производные по 
, то существует единственное решение уравнения (2), проходящее через точку М и определенное в некоторой окрестности точки х0.
Общим решением уравнения (1) или (2) называется такая функция
, которая при любых допустимых значениях произвольных постоянных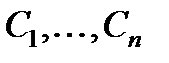 
является решением этого дифференциального уравнения и для любой задачи Коши с условиями (3) найдутся единственные значения этих постоянных.
Общим интегралом уравнения (1) или (2) называется соотношение
(4)
определяющее общее решение в неявном виде.
Решение, полученное из общего решения при фиксированных значениях произвольных постоянных, называется частным решением.
Аналогично определяется и частный интеграл при фиксированных значениях.
График любого частного решения уравнения (1) или (2) представляет собой линию, называемую интегральной кривой дифференциального уравнения. Общее решение (общий интеграл) представляет собой семейство интегральных кривых на плоскости, зависящее от п параметров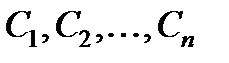 
.
