УДК 51(075.8)(076)
З-15
| З-15 | Составитель Н. А. Смирнова, старший преподаватель кафедры «Высшая математика» Рецензент Н. В. Ракита, доцент кафедры «Высшая математика» Рекомендовано к изданию на заседании кафедры ВМ 11.11.2008 г. Задания по математике в тестовой форме для организации самостоятельной работы: учеб.-метод. пособие. Часть I. Ижевск: Изд-во ИжГТУ, 2008. − 28 с. Методическое пособие разработано для использования при самоподготовке студентов к экзамену по дисциплине «высшая математика». Приведены задания в различных формах: открытой, закрытой и на установление соответствия. В конце издания указаны ответы. Пособие предназначено для студентов первого курса очной и заочной форм обучения инженерно-технических направлений ИжГТУ. УДК 51(075.8)(076) |
© Смирнова Н. А., составление, 2008
© Издательство ИжГТУ, 2008
I. Элементы векторной алгебры
1. Найти скалярное произведение векторов a и b, а ={1;  1;5}, b ={3;5;−8}.
1;5}, b ={3;5;−8}.
2. Найти векторное произведение векторов а и b, а ={1;  1;5}, b ={3;5;
1;5}, b ={3;5;  8}.
8}.
3. Выбрать пару коллинеарных векторов:
а) а ={1:  }, b ={
}, b ={  };
};
б) а ={2;  }, b ={2;
}, b ={2;  };
};
в) а ={4;6;  }, b ={
}, b ={  };
};
г) а ={0;1;1}, b ={1;0;0}.
4. Выбрать пару перпендикулярных векторов:
а) а = {1;  }, b = {3;5;
}, b = {3;5; 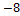 };
};
б) а = {1;  }, b ={4;9;1};
}, b ={4;9;1};
в) а ={0;1;0}, b ={1;0;  };
};
г) а ={2;7}, b ={  }.
}.
5. Выбрать тройки компланарных векторов:
а) а = {1;  }, b = {3;5;
}, b = {3;5; 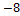 }, с = {1;
}, с = {1;  };
};
б) а ={1; 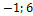 }, b ={
}, b ={  }, с ={1
}, с ={1  };
};
в) а ={1;2;3}, b ={4;5;6}, с ={7;8;11};
г) а ={1;0;0}, b ={0;1;0}, с ={0;0;1}.
6. Пусть m = 2а + 3b. Тогда, если а = {1;  }; b = {2;
}; b = {2;  }, то
}, то
а)  =
=  ;
;
б)  =2;
=2;
в)  =
=  ;
;
г)  1,5.
1,5.
7. Найти модуль вектора  , если А(12;
, если А(12;  ), В(16;0;
), В(16;0;  .
.
8. Найти направляющие косинусы для вектора а ={1;2  }.
}.
9. Найти площадь параллелограмма, построенного на векторах а и b:
а ={1; 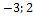 }, b ={2;0;
}, b ={2;0;  }.
}.
10. Вычислить площадь треугольника АВС, где А(1;2;0), В(3;2;1), С( 2;1;2).
2;1;2).
11. Вычислить объем пирамиды АВСД, где А(5;1;  4), В(1;2;
4), В(1;2;  1), С(3;3;
1), С(3;3;  4), Д(2;2;2).
4), Д(2;2;2).
12. Указать левую тройку векторов:
а) а ={  }, b ={
}, b ={  }, с ={1;
}, с ={1;  };
};
б) а ={  }, b ={
}, b ={  }, с ={
}, с ={  };
};
в) а ={0;3;0}, b ={4;0;0}, с ={0;0;5}.
13. Выбрать утверждение, не соответствующее определению векторного произведения:
а) векторным произведением векторов а и b является вектор с, перпендикулярный векторам а и b;
б)  =
=  ;
;
в) векторным произведением векторов а и b является вектор с, коллинеарный векторам а и b;
г) векторы а, b, с образуют правую тройку.
14. Орт вектора по определению:
а) проекция вектора на ось ОХ;
б) направление вектора;
в) единичный вектор, имеющий одинаковое направление с данным;
г) любой вектор единичной длины.
15. Заданы векторы: а ={1;1;3}, b ={2;2;1}, с ={2;2;  14}.
14}.
Разложить вектор с по базису а, b.
16. Выбрать правильный ответ.
Вектор а ={2;5}повернули на 90° против часовой стрелки, его новые координаты:
а) {  };
};
б) {  };
};
в) {5;  };
};
г) {  }.
}.
II. Элементы линейной алгебры
1. Выбрать правильный ответ. Обратная матрица существует:
а) для любой матрицы;
б) для любой квадратной матрицы;
в) для квадратной матрицы, определитель которой не равен нулю;
г) для квадратной матрицы, определитель которой неотрицателен.
2. Какое из нижеперечисленных свойств не является свойством определителя:
а) если две строки (два столбца) поменять местами, то знак определителя изменится на противоположный;
б) чтобы умножить определитель на число, нужно умножить на это число каждый элемент определителя;
в) определитель равен сумме произведений элементов строки (столбца) и их алгебраических дополнений;
г) если к какой-либо строке (столбцу) определителя прибавить линейную комбинацию других строк, то определитель не изменится?
3. Выбрать все правильные ответы.
Элементарным преобразованием матрицы является:
а) перемена местами двух строк или столбцов;
б) умножение элементов строки (столбца) на число;
в) транспонирование;
г) прибавление к элементам строки (столбца) линейной комбинации параллельных строк (столбцов).
4. Какой из определителей равен 7?
а)  ; б)
; б) 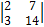 ; в)
; в)  ; г)
; г)  .
.
5. Выбрать правильное.
(Aij – алгебраическое дополнение элемента aij определителя Δ).
а) Δ = а21А11 + а22А12 + а23А13;
б) Δ = а11А21 + а12А22 + а13А23;
в) Δ = а11А11 + а21А12 + а31А13;
г) Δ = а21А21 + а22А22 + а23А23.
6. Вычислить определитель:  .
.
7. Установить правильное соответствие:
| а) матрицу преобразовали так, что столбцы стали строками; | 1) симметричная матрица; | |
| б) в матрице все элементы равны нулю; | 2) невырожденная матрица; | |
| в) определитель матрицы не равен нулю; | 3) нулевая матрица; | |
| г) матрица составлена из алгебраических дополнений её элементов и транспонирована; | 4) кососимметричная матрица; | |
| д) в матрице элементы, стоящие на главной диагонали, равны единице, остальные - нули; | 5) присоединенная матрица; | |
| е) матрица равна транспонированной; | 6) транспонированная матрица; | |
| ж) все элементы матрицы равны единице; | 7) обратная матрица; | |
| з) матрица равна транспонированной со знаком «минус»; | 8) единичная матрица. | |
| и) при умножении на эту матрицу получается единичная. |
8. Установить правильное соответствие:
| а) система линейных уравнений имеет единственное решение, если | 1) ранг расширенной матрицы равен рангу основной матрицы системы и меньше числа неизвестных; |
| б) система линейных уравнений не имеет решений, если | 2) ранг расширенной матрицы больше ранга основной матрицы системы; |
| в) система линейных уравнений имеет множество решений, если | 3) ранг расширенной матрицы равен рангу основной матрицы системы и равен числу неизвестных. |
9. Исследовать систему на совместность

10. Укажите все пары матриц, которые можно перемножить между собой:
A =  .
.
11. Найти произведение матриц А и В:
А = 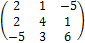 ; В =
; В = 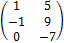 .
.
12. Найти обратную матрицу для А, если А =  .
.
13. Найти ранг матрицы В =  .
.
14. Решить матричное уравнение AXB=C, если
A =  , B =
, B =  , C =
, C =  .
.
15. Решить систему линейных уравнений по формулам Крамера:

16. Выбрать правильный ответ.
Собственные числа и собственные векторы матрицы А =  :
:
а) λ = 1, r =  ; б) λ = −2, r =
; б) λ = −2, r = 
в) λ = 2, r = 






