б) 
Лопиталь ережесі арқылы анықталмағандықты ашу. Теорема (Лопиталь ережесі). f(x) және g(x) функциялары 
(
) жағдайда нолге немесе шексіздікке ұмтылсын. Егер олардың туындыларының қатынасының шегі (ақырлы не ақырсыз) бар болса, функциялар қатынасының да шегі бар болады және мына қатынас орындалады: 
. Лопиталь ережесін қолданып ектерді есмептейік.
1. 
.
2. 
3. 
.
Үшінші мысалда Лопиталь ережесін бірден қолдануға келмейді. Сондықтан, алгебралық түрлендіру көмегімен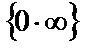 
түріндегі анықталмағандықты 
немесе 
түріндегі анықталмағандықтарға келтіреміз. Осы мақсатпен х 2 бөлімнің бөліміне түсірілді.
4. 
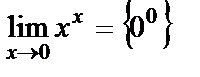. Айталық 
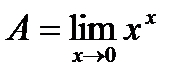деп белгілеп, теңдеудің екі жағын логарифмдейік. Теңдеудіңоңжағынесептейік: 
Туынды ұғымы.
1) Туынды анықтамасы. 
функциясы І аралығында анықталынсын. Егер x 0 ÎІ үшін 
ақырлы шегі бар болса, онда ол шекті функциясының x 0нүктесіндегі туындысы деп, 
символымен белгілейді.
Туынды табу амалын функцияны дифференциалдау дейді. Сонымен, анықтама бойынша
.
Басқаша сөзбен анықтама былай айтылады: Егер функцияның өсімшесінің өзінің пайда болуына себепші болған тәуелсіз айнымалының өсімшесіне қатынасының соңғы өсімше нольге ұмтылғанда ақырлы шегі бар болса, онда функцияны дифференциалданатын деп, сол шекті функцияның туындысы деп атайды.
Дәл осы сияқты, функциясының х 0 нүктесіндегі сәйкес сол және оң жақты туындыларының анықтамасына келеміз:
Демек, функциясының х 0 нүктесінде туындысы бар болуы үшін, оның ол нүктеде сол және оң жақты туындылары бар болып, олар өзара тең болуы қажетті және жеткілікті.
¦ функциясының графигін, яғни жазықтықта жатқан (x, f (x)) түріндегі нүктелер жиынын қарастырайық (оны y = f (x) қисығы не жай қисық деп те атайды).
Белгілі бір (x 0, f (x 0)) нүктесінде қисыққа «тығыз орналасқан» түзуді сызу. Әрине, ондай түзу бар болса, онда ол тек қана сол қисыққа тән қасиеттер арқылы табылады. Сондықтан, қисықта жатқан басқа (x 1, f (x 1)) нүктесін алып, сол екі нүктеден түзу өткізейік. Оның теңдеуі
болады. Әрбір (x 0, f (x 0)) нүктесінен өтетін және y -тер осьіне паралель емес түзудің теңдеуі y = k (x - x 0)+ f (x 0) түрінде жазылады, демек k нақты санына тәуелді болады.
Әрине, белгілі бір мағынада екі түзудің жақындығын оларды анықтайтын k сандарының жақындығы арқылы түсінуге болады. Ал, бізідң жағдайда сондай k сандары x 1-ге мынадай тәуелділікте болады.
Сондықтан, x 1-ді x 0-ге ақырсыз жақын алған сайын, k (x 1) белгілі бір k санына ақырсыз жақындаса, онда теңдеуі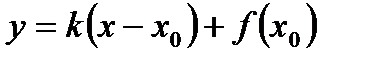 
болатын түзуді бізге керекті «қисыққа тығыз орналасқан» түзу ретінде алуға болады.
Мұндағы k -ны тапқан жолымыз шектер тілінде былай бейнеленеді.
яғни 
.
Айтқанымыздың геометриялық бейнесі 36-суретте берілген. Сонымен келесі анықтамаға келдік. Егер 
нүктесінде 
нақты мәнді шегі бар болса, онда 
түзуі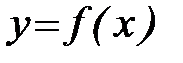 
қисығының нүктесіндегі жанамасы деп аталады.
Жылдамдық туралы есеп. Материялық нүкте түзу бойымен белгілі бір бағытта қозғалып келе жатсын. Оның түзу бойындағы белгілі бір нүктеден 
мезгіліндегі ара қашықтығы 
болсын.
Әуелі 
болсын, яғни нүкте бірқалыпты қозғалсын. Онда кез келген 
мен 
мезгілдері арасында нүкте 
жолын жүреді, ал 
қатынасы сол қозғалыстың жолы деп аталады да, тұрақты болып, а санына тең болады.
Егер нүктенің қозғалысы бірқалыпты болмаса, онда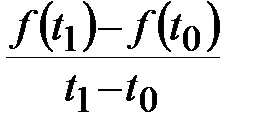 
қатынасы тұрақты болмай мен мезгілдеріне тәуелді болады. Ол мен мезгілдері арасындағы материялық нүктенің орташа жылдамдығы деп аталады.
Расында, орташа жылдамдығы нүктенің мен мезгілдері арасында қандай жылдамдықпен қозғалғаны туралы ешқандай әсер бермейді, өйткені ол бір мезгіл жылдам, бір мезгіл жай қозғалуы мүмкін. Орташа жылдамдық мағынасы мынада: егер нүкте сол арада бірқалыпты қозғалса, онда 
мезгілінде 
жолын жүру үшін оның жылдамдығы орташа жылдамдыққа тең болуы тиіс.
Егер -ді 
-ге ақырсыз жақындатқанда, оған сәйкес орташа жылдамдығы белгілі бір нақты санға ақырсыз жақындаса, онда сол санды мезгіліндегі нүктенің жылдамдығы түрінде алған жөн.
Сонымен, айтқанымызды шек арқылы бейнелесек, мына анықтамаға келеміз: егер
нақты мәнді шегі бар болса, онда оны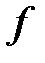 
тәртібі арқылы бейнеленген қозғалыстың нүктесіндегі жылдамдығы деп атайды.
Айталық,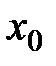 
нүктесінде және оның төңірегінде 
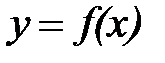функциясы анықталған болсын.
Анықтама. Аргумент 
- тің 
нүктедегі өсімшесі деп 
айырымын айтады.
Анықтама. 
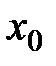функциясының нүктедегі өсімшесі деп мына
айырманы айтады
Бұл өсімше екі 
және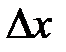 
аргументтерге тәуелді. Геометриялық тұрғыда 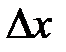және 
функция графигі бойымен 
нүктеден 
нүктеге дейін жылжығанда, нүктенің абсцисасы мен ординатасының өзгеруін көрсетеді.
Мысалы, егер 
болса, онда 
, яғни қабырғасы 1- ге тең шаршының қабырғасын 0,1- ге арттырсақ, онда оның ауданы 0,21- ге артады.
Анықтама. Егер 
функциясы 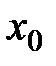нүктенің төңірігінде анықталған және 
болса, онда ол 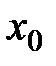үзіліссіз деп аталады.
Шындығында да, 
.
A
Анықтама. Егер 
бар болса, онда бұл сан 
функциясының нүктедегі туындысы деп аталады.
Бұл туынды мына символдардың бірімен белгіленеді:
.
.
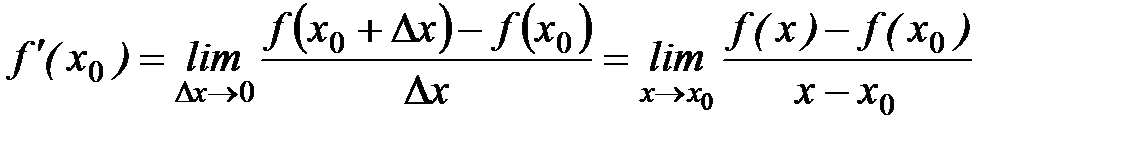Анықтама. Егер 
функциясы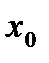 
нүктеде шекті туындыға ие болса, онда ол осы нүктеде дифференциалданады деп аталады.
Енді функцияның дифференциалымен оның үзіліссіздігінің арасындағы байланысты анықтайық, ол үшін бұл анықтамада 
- ті ажыратамыз.
,
Сондықтан
.
Теорема. Егер 
функциясының 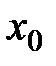нүктеде дифференциалы бар болса, онда ол бұл нүктеде үзіліссіз болады.
Кері тұжырым дұрыс емес, мысалы,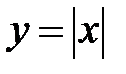 
функциясы анықталу облысының барлық нүктелерінде үзіліссіз, бірақ ол 
нүктесінде дифференциалданбайды, себебі 
. 
, ал бұл шек жоқ.
