Матрица және матицаларға амалдар қолдану.
Анықтама. m жатық n тік жолдан құрылған кестені mxn өлшемді матрица деп атайды.
Матрицаны құрайтын сандар матрица элементтері деп аталады. Әдетте матрица латын алфавитінің бас әріптерімен, ал элементтері сәйкес кіші әріптермен белгіленеді:
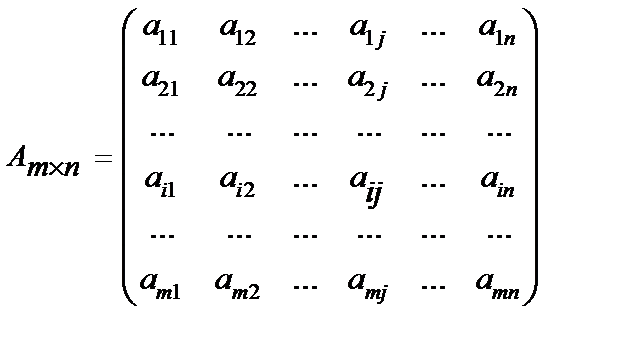
Қысқаша жазылуы:
Матрица элементінің бірінші индексі жатық жол нөмірі, ал екінші индексі тік жол (бағана) нөмірін көрсетеді. Мысалы, 
элементі екінші жатық жол мен үшінші тік жол қиылысында орналасқан.
Бір ғана жатық жолдан құралған матрицаны жол-матрица, ал бір ғана тік жолдан құралған матрицаны бағана-матрица депатайды:
- жол-матрица;
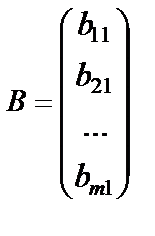- бағана матрица.
Жол матрица мен бағана матрицаны кейде вектор деп те айтады..
Жатық жолдар саны мен тік жолдар саны тең болатын матрица квадрат матрица деп аталады,
.
Квадрат матрицаның 
элементтері диагоналдық элементтер деп аталады да, матрицаның негізгі диагоналін құрайды. Ал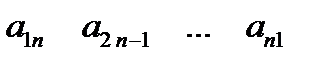 
элементтері қосымша диагоналдық элементтер деп аталады да, матрицаның қосымша диагоналін құрайды.
Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,
, 
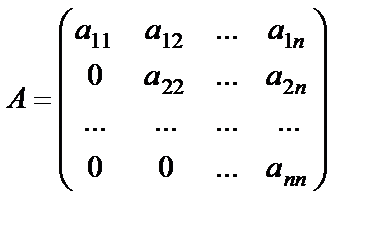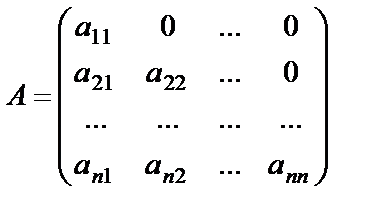
Диагоналды емес элементтерінің бәрі нолге тең болатын квадрат матрица диагоналды матрица деп аталады,
.
Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,
.
Барлық элементтері нолге тең матрица нолдік матрица деп аталады.
МАТРИЦАЛАРҒА ҚОЛДАНЫЛАТЫН АМАЛДАР
В)Матрицаларды қосу және алу. Өлшемдері бірдей матрицаларды ғана қосуға болады.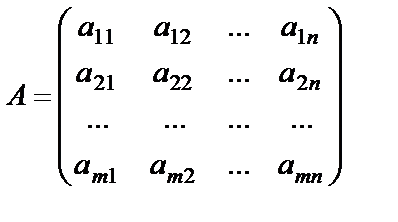 
және 
матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз:
.
Мысалы, 
мен 
матрицаларын қосайық:
.
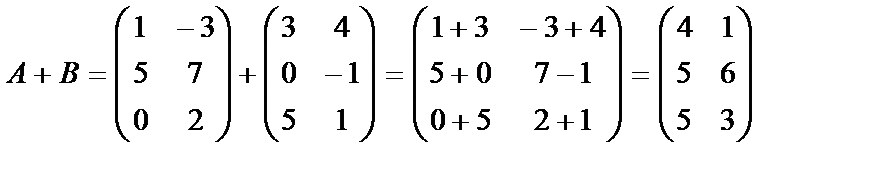А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті:
A – B = A+(-1)B
немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады. Мысалы А матрицасынан В матрицасын алайық:
.
С)Матрицаны санға көбейту. Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:
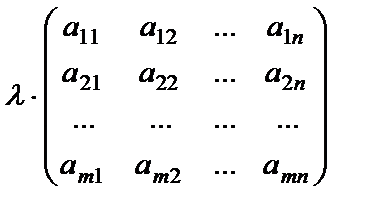
Мысалы,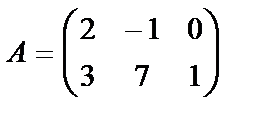 
матрицасын 
санына көбейтейік:
.
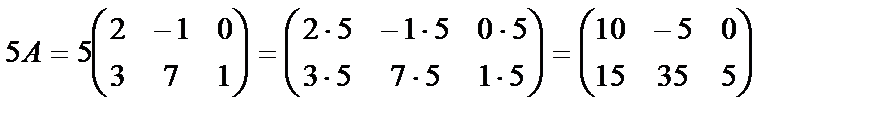Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
Д) Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі m x k болатын А матрицасы мен өлшемі k x n болатын В матриасы берілсін:
Осы екі матрицаны көбейткенде өлшемі m x n болатын көбейтінді С матрица аламыз:
С матрицасының 
элементі А матрицаның 
–жатық жол элементтерін В матрицаның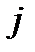 
–тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:
, 
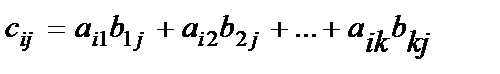. (1)
Мысалы,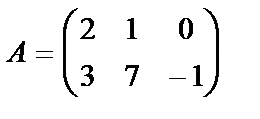 
матрицасы мен 
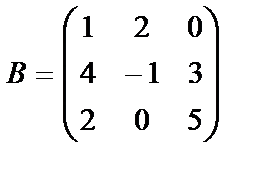матрицасын көбейтейік. Бірінші матрица үш тік жолдан, ал екінші матрица үш жатық жолдан тұрғандықтан бұл матрицаларды көбейтуге болады. Көбейтінді матрицаның өлшемін анықтайық:
,
яғни, 
. k=3 болғандықтан (1) формуланы қолданғанда үш қосылғыш болады:
, 
.
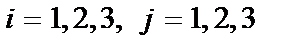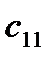элементін табу үшін формуладағы i=1, j=1 деп аламыз, сонда
,
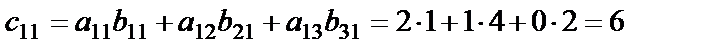яғни А матрицаның 1-жатық жол элементтерін В матрицаның 1-тік жолының сәйкес элементтеріне көбейтіп қостық. Осылай С матрицаның барлық элементтері табылады:
C=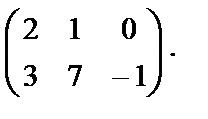 
= 
= = 
.
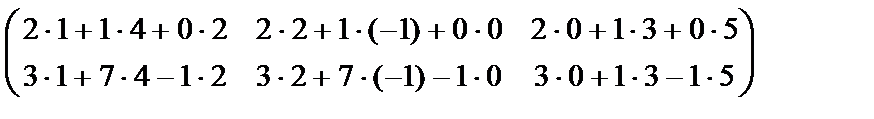Қосу және көбейту амалдарының мынадай қасиеттері бар:
| 1) A+B=B+A | 5) (A+B)C=AC+BC |
| 2) (A+B)+C=A+(B+C) | 6)  (AB)=( A)B=A( B)
|
| 3) (A+B)= A+ B
| 7) A(BC)=(AB)C |
| 4) A(B+C)=AB+AC | |
Бұл қасиеттер сандарға жасалатын амалдар қасиеттеріне ұқсас. Енді матрицаның өзіндік ерекшелігіне байланысты қасиеттерін қарастырайық.
8) Біріншіден, екі матрицаның АВ көбейтіндісі болғанмен ВА көбейтіндісі болмауы мүмкін. Мысалы,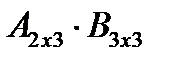 
көбейтіндісі бар, бірақ 
көбейтіндісі жоқ, себебі бірінші матрицаның тік жолдар саны екінші матрицаның жатық жолдар санына тең емес;
екіншіден, АВ және ВА көбейтінділері бар болғанмен, олардың өлшемдері әртүрлі болуы мүмкін. Мысалы,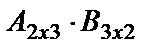 
және 
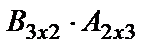көбейтінділер бар, бірақ өлшемдері әртүрлі:
, 
;
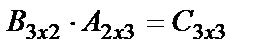үшіншіден, АВ және ВА көбетінділер бар және олардың өлшемдері бірдей болғанмен, жалпы жағыдайда, көбейтудің коммутативті заңы орындалмайды, яғни АВ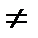 
BA.
Мысал. 
мен 
матрицалары берілген. АВ және ВА көбейтінділерін табау керек.
Шешуі. Берілген матрицалар өлшемдері 2 х 2 квадрат матрицалар, оларды көбейтуге болады:
.
.
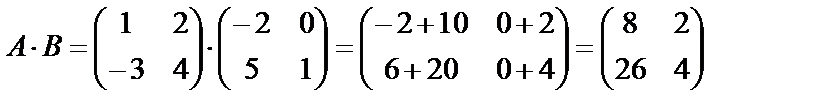Көріп отырғанымыздай АВ 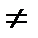BA.
9) А -квадрат матрица болса, онда мына теңдік орындалады:
АЕ = ЕА = А.
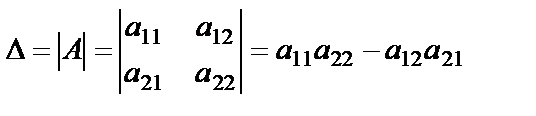
Мысалы,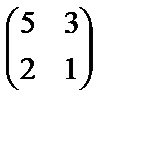 
матрицаның анықтауышын есептейік:
.
2. 2 ретті анықтауыштар, қасиеттері. 
-ші ретті анықтауыш немесе детерминант деп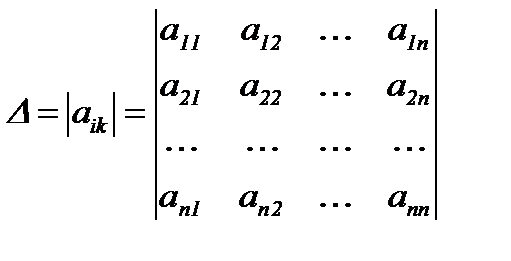 
түрінде жазылған және төмендегідей формуламен есептелінетін санды айтамыз:
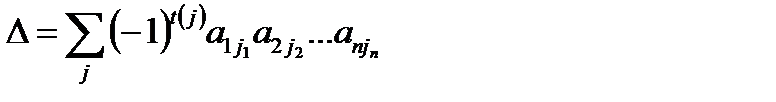(2)
мұндағы қосынды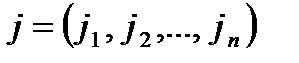 
алмастыруындағы ретсіздіктер саны
демек 2 ретті анықтауыш: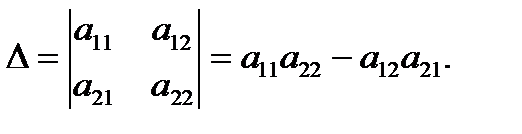 
a11, a12,a21,a22- анықтауыштың элементтері. а11 және а22 бас диагональді құрайды, а12 және а 21 – қосымша диагональдың элементтері.Немесе 2ретті анықтауышарды Екі белгісізі бар сызықтық екі теңдеу жүйесін құрастыру арқылы да қорытып шығаруға болады.Мысалы Ол үшін 
Белгісіздерді анықтау үшін бірінші теңдеуді а 22 көбейтіп, ал екінші теңдеуді- a12 көбейтіп екі теңдеуді қосып белгісіз х-ті табамыз. (a11a22-a12a21)x=b1a22-b2a12oсындай операцияны жасап белгісіз у-ті анықтаймыз: (a11a22-a12a21)y=b22a22-b1a21.Соңғы екі теңдеулерден х және у айнымалыларды анықтаймыз:
(1.2) формулалардапайдаболған a11a22-a12a21, b22a22-b1a21, a11b2-b1a21
өрнектерді 2-шіреттіанықтауыштардепатайды. Яғни: 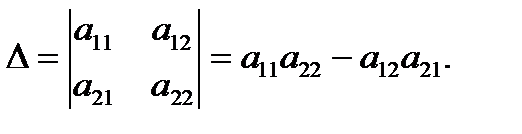Көріп отырғанымыздай дәл екінші анықтамадағыдай өрнек шығып отыр.
Айнымалылардың алдында тұрған коэффициентерінен құрылған анықтауышын жүйенің бас анықтауышы деп атайды. Ал ∆х анықтауышы бас анықтауыштың бірінші бағандағы элементтерін жүйенің бос мүшелерімен алмастырылып құралады, ал - ∆y екінші бағанның элементтерін бос мүшелерден құралған бағанмен алмастырады.
(1.4) формуларынКрамерформуласыдепатайды.Мысалы:
Анықтауыштың негізгі қасиеттері:
1. Анықтауыштың жолдарын оның сәйкес бағандарымен орын алмастырғаннан ол анықтауыштың сан мәні өзгермейді.
2. Егер анықтауыштың екі жолын (бағанын) бірімен-бірінің орындарын алмастырса онда анықтауыш таңбасы қарама-қарсы таңбаға ауысады.
3. Егер анықтауыштың кез-келген екі жолы өзара тең болса, онда ол нөлге тең болады.
4. Егер анықтауыштың қандай да болса бір жолының барлық элементтері нөлге тең болса, онда анықтауыш нөлге тең болады.
5. Анықтауыштың жолының немесе бағанының элементтерінің ортақ көбейткішін анықтауыш алдына шығаруға болады.
6. Егер анықтауыштың екі жолының элементтері өзара пропорционал болса онда анықтауыш нөлге тең.
7. Анықтауыштың қандай да болса бір жолының элементтерін олардың сәйкес алгебралық толықтауыштарына көбейтіп қосқаннан шыққан қосынды анықтауыш шамасына тең болады.
8. Егер анықтауыштың бір жолының элементтері екі қосылғыш арқылы берілген болса, онда анықтауыш екі анықтауыштың қосындысына тең болады. Бірінші анықтауыштың сәйкес жолында бірінші қосылғыш, екінші анықтауышта екінші қосылғыш.
9. Егер анықтауыштың қандай болса да бір жолының элементтерін бір ғана санына көбейтіп басқа бір жолының сәйкес элементтеріне қосса, онда бұдан анықтауыш шамасы өзгермейді.
Ші ретті анықтауыш
в)3-ші ретті анықтауыш
үшінші ретті матрицаға 
үшінші ретті анықтауыш сәйкес келеді:
.
Бұл анықтауыштың есептелуін үшбұрыш ережесі немесе Саррус ережесімен оңай есте сақтауға болады. Бұл ереже бойынша алғашқы оң таңбалы үш қосылғыш 1-схема, ал кейінгі теріс таңбалы үш қосылғыш 2-схемамен есептелінеді.
1-схема 2-схема
3.3-ші ретті анықтауыш
Мысалы, мынадай үшінші ретті анықтауышты есептейік:
Реті үштен көп болатын анықтауыштарды есептеу үшін жаңа ұғымдар қажет болады.
А)Анықтама. n-ретті квадрат матрицаның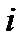 
–жатық жолы мен 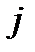–тік жолын сызып тастағаннан кейін пайда болған (n–1)-ретті анықтауышты 
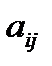элементінің миноры деп атайды және 
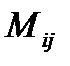деп белгілейді.
Үшінші ретті марицаның 
элементінің миноры мынадай екінші ретті анықтауыш болады:
.
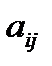элементінің алгебралық толықтауышы деп мынадай санды айтады:
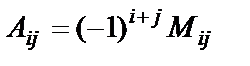
Үшінші ретті марицаның элементінің алгебралық толықтауышы мынадай сан:
Мысалы, 
матрицасының бірінші жатық жолдағы элементтерінің миноры мен алгебралық толықтауыштарын есептейік:
, 
, 
,
, 
,
, 
, 
.
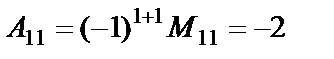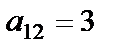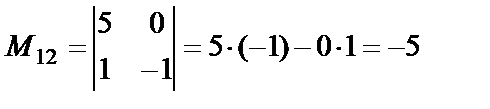
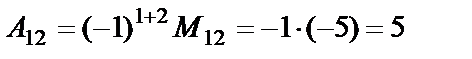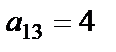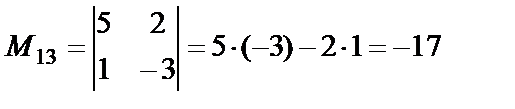Лаплас теоремасы. 
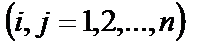квадрат матрицаның Δ анықтауышы оның кез келген жол элементтерін сәйкес алгебралық толықтауыштарға көбейтіп қосқанға тең:
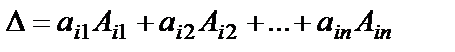
- бұл анықтауыштың i –жатық жолы бойынша жіктелініп есептелуі.
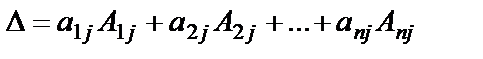
- бұл анықтауыштың j –тік жолы бойынша жіктелініп есептелуі.
Алдыңғы мысалдағы 
матрицасының анықтауышын бірінші жатық жолы бойынша жіктеп есептейік:
,
мұндағы алгебралық толықтауыштардың дайын мәндерін алдыңғы мысалдан алдық.
С)Лаплас теоремасы n -ретті анықтауыш есептеуді (n-1)-ретті анықтауыш есептеуге келтіріледі. Сонымен, кез келген n -ретті (n>3) анықтауышты дәрежесін төмендету арқылы екінші ретті анықтауышты есептеуге келтіруге болады екен.
Д)Енді анықтауыш қасиеттерін қарастырайық.
1-қасиет. Анықтауыштың жатық жолдарын сәкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен, анықтауыш мәні өзгермейді:
.
Теңдіктің дұрыстығын анықтауыштарды есептеу арқылы тексеруге болады.
2-қасиет. Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. Үшінші ретті анықтауыштың екінші жолындағы ортақ көбейткішті анықтауыш алдына шығарамыз:
.
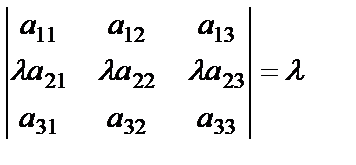
Теңдіктің дұрыстығына берілген матрицаны екінші жол бойынша жіктеп тексеруге болады.
3-қасиет. Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. Үшінші ретті анықтауыштың бірінші және екінші жолдарын алмастырайық:
Теңдіктің дұрыстығын екінші анықтауышты бірінші жол бойынша жіктеп тексеруге болады.
4-қасиет. Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нолге тең. Үшінші ретті анықтауыштың бірінші және екінші жолдары бірдей болсын:
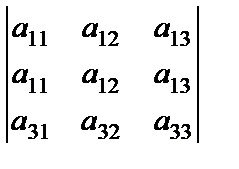=0.
Теңдіктің дұрыстығын осы екі жолдың орндарын алмастырып 3-қасиетті қолданып тексеруге болады.
5-қасиет. Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді. Үшінші ретті анықтауыштың бірінші жолын 
-ға көбейтіп екінші жолға қосайық:
.
Теңдіктің дүрыстығын екінші анықтауышты мынадай
+ 
анықтауыштардың қосындысы түрінде жазайық. Сонда бірінші қосылғыш берілген анықтауыш болады да, екінші анықтауыш нолге тең.
6-қасиет. Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісіне тең:
.
Теңдіктің дұрыстығын анықтауышты бірінші тік немесе үшінші жатық жол бойынша жіктеп тексеруге болады.
Осы қасиеттер көмегімен жоғары ретті анықтауыштар есептеуді көп жеңілдетуге болады. Анықтауышты қандай да бір жолында неғұрлым көп ноль болатындай етіп түрлендіріп, сол жол бойынша жіктеп анықтауыш реті төмендетіледі. Мысалы мынадай төртінші ретті 
анықтауышты есептейік.
Анықтауышты үшбұрышты түрге келтіреміз. Алдымен 5-қасиет бойынша анықтауыштың бірінші жолын 1-ге көбейтіп үшінші жолға, (-1)-ге көбейтіп төртінші жолға қосайық (есепте көрсетілген). Сонда анықтауыштың бірінші тік жолында 
элементтен басқасы нолге айналады.
Енді осы қасиетті пайдаланып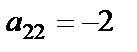 
элементінің астында тұрған сандарды нолге айналдырамыз. Соңында 
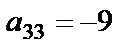элементінің астында тұрған сандарды нолге айналдырамыз. Анықтауыш үшбұрышты түрге келді. 6-қасиет бойынша анықтауыш мәнін диагональдік элементтерді көбейтіп табамыз.
= 
=
= 
= 
.
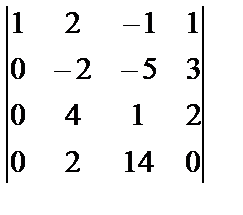
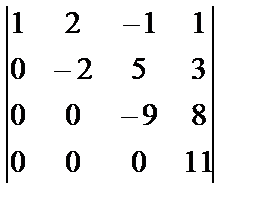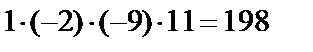