Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады. Оқулықтарда векторларды 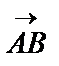 немесе
немесе 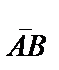 , кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді (
, кейде тек қалың әріптермен АВ белгілеу түрлері кездеседі. Сол сияқты векторларды бір әріппен де белгілей береді (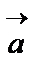 =
= 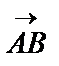 ,
, 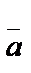 , а).
, а).
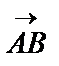 векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және
векторының ұзындығы деп АВ кесіндісінің ұзындығын айтады және 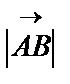 деп белгілейді.
деп белгілейді.
Басы мен соңы беттесетін вектор нолдік вектор деп аталады,  =
= 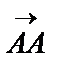 және ұзындығы нолге тең.
және ұзындығы нолге тең.
Бір түзудің не өзара параллель түзулер бойында орналасқан векторлар коллениар векторлар деп аталады.
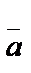 және
және 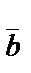 векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:
векторларының қосындысы «үшбұрыш» не «параллелограмм» ережесімен анықталады:

|
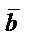
|
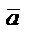
|
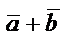
|

|

|
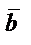
|

|
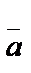 және
және 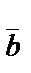 векторларының
векторларының 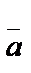 -
- 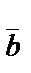 айырымы деп
айырымы деп 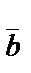 -ға қосқанда
-ға қосқанда 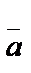
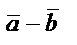
|
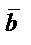
|
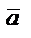
|
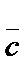 =
= 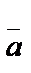 -
- 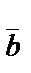 векторын айтады.
векторын айтады.
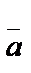 векторының
векторының 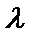 санға көбейтіндісі деп ұзындығы
санға көбейтіндісі деп ұзындығы 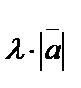 болатын, бағыты
болатын, бағыты 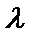 >0 болғанда
>0 болғанда  векторымен бағыттас,
векторымен бағыттас, 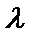 <0 болғанда
<0 болғанда 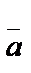 векторымен қарама-қарсы бағытта болатын
векторымен қарама-қарсы бағытта болатын 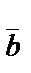 векторын айтады. Суретте,
векторын айтады. Суретте, 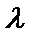 = 2,
= 2, 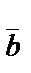 =2
=2 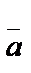 ;
; 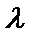 = -1,
= -1, 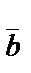 =-
=- 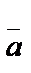 .
.
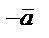
|
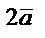
|

|
Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусына көбейтіндісіне тең шаманы айтады:
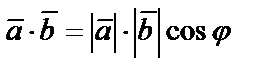 .
.
| A |
| y2 y1 |
| 0 x1x2 x |
| B |
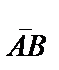 векторының басы мен соңының координаталары белгілі болсын
векторының басы мен соңының координаталары белгілі болсын 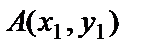 және
және 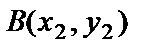 . Сонда
. Сонда 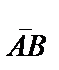 векторын координаталары арқылы былай жазуға болады:
векторын координаталары арқылы былай жазуға болады:
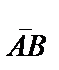 =
= 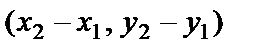
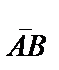 векторының басы координаталар басымен беттесетіндей етіп өз-өзіне параллель көшірсек, онда
векторының басы координаталар басымен беттесетіндей етіп өз-өзіне параллель көшірсек, онда 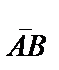 векторының координатасы вектордың соңының координаталарымен бірдей болатынын аңғару қиын емес.
векторының координатасы вектордың соңының координаталарымен бірдей болатынын аңғару қиын емес.
Жазықтықта вектордың координатасын екі сан анықтаса, айталық  , кеңістікте үш сан анытайды,
, кеңістікте үш сан анытайды, 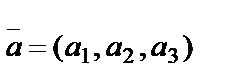 .
.
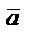
|
| a 2 y |
| a1 x |
| z a3 |
| a 1 x |

|
| a2 |
| y |
Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең:
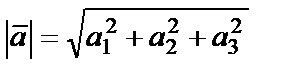 .
.
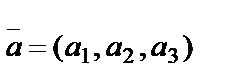 және
және  векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады:
векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады:
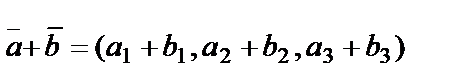
Ал 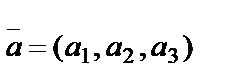 векторын
векторын 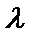 санға көбейту мынадай түрде анықталады:
санға көбейту мынадай түрде анықталады:
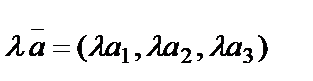
Ал 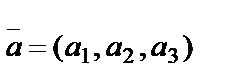 және
және  векторларының скаляр көбейтіндісі мынадай:
векторларының скаляр көбейтіндісі мынадай:
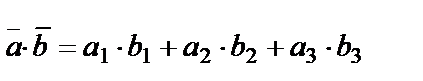
Енді векторлық кеңістік ұғымына көшейік. Элементтері x, y, z, … болатын қандай да бір R жиын қарастырайық. Осы жиынның кез келген x және y элементтері үшін қосу x + y амалы мен қандай да бір х элементі және  нақты сан үшін көбейту
нақты сан үшін көбейту  х амалы орындалсын.
х амалы орындалсын.
Анықтама. R жиынның элементтерін қосу және элементін нақты санға көбейту амалдары төмендегідей шарттарды қанағаттандырса, R жиын векторлық (сызықтық) кеңістік деп, ал элементтерін векторлар деп атайды:
1. x+y=y+x;
2. (x+y)+z=x+(y+z);
3. Кез келген x  R үшін 0
R үшін 0 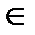 R (нол-элемент) табылады да, мынадай қатынас орындалады: x+0=x;
R (нол-элемент) табылады да, мынадай қатынас орындалады: x+0=x;
4. Кез келген x 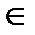 Rүшін -х
Rүшін -х 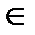 R (қарама-қарсы элемент)табылады да, мынадай қатынас орындалады: x+(-x)= 0;
R (қарама-қарсы элемент)табылады да, мынадай қатынас орындалады: x+(-x)= 0;
5. 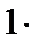 x=x;
x=x;
6. 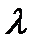 (
( x)=(
x)=(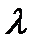
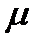 )x;
)x;
7. 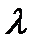 (x+y)=
(x+y)= 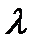 x+
x+ 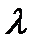 y
y
8. (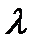 +
+  )x=
)x= 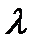 x+
x+ 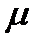 x.
x.
x және y векторларының айырмасы деп х векторы мен –1у векторларының қосындысын айтамыз:
x-y=x+(-1)y
Векторлық кеңістіктің анықтамасынан кез келген х векторды 0 нақты санына көбейткенде пайда болатын жалғыз 0 - ноль вектордың бар болатындығы; әрбір х вектор үшін осы векторды (-1) санына көбейткенде пайда болатын жалғыз қарама-қарсы (–х) вектордың бар болатындығы шығады.




