Предположим, что задан непрерывный марковский процесс
и имеются непрерывные измерения
, 
где 
-интенсивность белошумной ошибки измерений.
В рамках теории линейной фильтрации показано, что оценку с минимальной ковариационной матрицей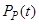 
можно получить с использованием выражений
,
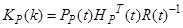
получивших название непрерывного фильтра Калмана.
Заметим, что выражение для оценки можно преобразовать к виду
которое можно трактовать как уравнение динамической системы с сигналом на входе системы 
Для непрерывного фильтра Калмана можно получить дифференциальное уравнение для ошибки оценки
и, как следствие, можно получить следующее выражение для действительной ковариационной матрицы ошибки оценки
Использование непрерывного фильтра для исследования качества дискретного фильтра
Выражения для непрерывного фильтра оказываются проще соответствующих выражений для дискретного фильтра. В этой связи измерения в дискретном фильтре можно трактовать как непрерывные измерения, сглаженные на интервале дискретности. С учетом такого сглаживания можно установить следующую связь между параметрами дискретного и непрерывного фильтра
и, как следствие,
.
И далее использовать для анализа непрерывный фильтр Калмана
Представление детерминированных процессов с помощью системы базисных функций
В общем случае процесс требует для своего описания достаточно сложных функций. Одним из подходов упрощения описания процесса является его замена комбинацией более простых функций, т.е. аппроксимация сложной функции с использованием базисных функций.
Пусть функция 
абсолютно интегрируема на рассматриваемом интервале 
. Эта функция может быть разложена по некоторой системе базисных функций 
в том же интервале, т.е. представлена в виде
.
Если выбрана система базисных функций, то описание процесса полностью определяется совокупностью коэффициентов 
, которые называют спектром процесса.
При решении практических задач приходится учитывать конечное количество членов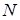 
. При этом заданная функция будет представлена приближенно, как
(**),
Базисные функции выбираются исходя из априорной информации об исследуемом сигнале так, чтобы они имели простое аналитическое выражение, обеспечивали быструю сходимость и позволяли легко вычислять коэффициенты
Эти коэффициенты рассчитываются из условия, чтобы некоторый заранее выбранный критерий приближения принимал наименьшее значение.
