Рассмотрим ошибку оценки
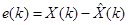
и ковариационную матрицу ошибки оценки
.
При синтезе оптимального фильтра будем добиваться, чтобы ковариационная матрица оптимального фильтра удовлетворяла неравенству
, (*)
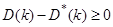где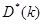 
-ковариационная матрица ошибки оптимальной оценки 
.
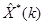Введем обозначения: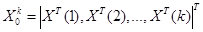 
, 
.
В теории оптимального оценивания получен следующий фундаментальный результат: оптимальная оценка в смысле выполнения неравенства (*), как неравенства квадратичных форм, существует и представляет собой условное математическое ожидание вектора состояния, записываемое в виде
, (**)
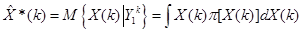где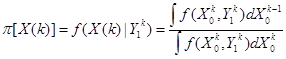 
-условная (апостериорная) плотность вектора 
, а 
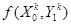- совместная плотность распределения векторов 
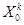и 
.
Здесь и далее, интегралы понимаются как многомерные, а дифференциалы от векторов- как произведения дифференциалов их компонент, при этом совместная плотность 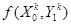понимается как совместная плотность вектора состояния динамической системы и измерений в последовательные моменты времени 0,1,2,…… 
: 
.
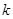Действительно, пусть 
оценка, выработанная любым фильтром
Ошибке этой оценки придадим вид
Где 
Заметим, что математическое ожидание берется по совокупности случайных величин и найти его можно последовательно
.
Условную ковариационную матрицу ошибки оценки 
запишем в виде
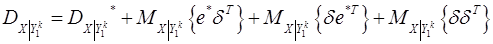
Рассмотрим второе слагаемое
.
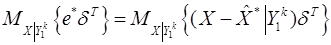Используя тот факт, что по предположению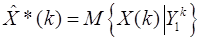 
получим, что
, 
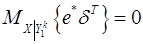=0 и
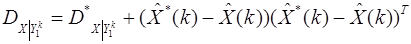
Проводя теперь осреднение по множеству измерений, также получаем связь между средними ковариационными матрицами
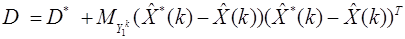
Отметим, что из неравенства (*), понимаемого как неравенство квадратичных форм, вытекает ряд свойств ошибок оптимальной оценки, важных для практических, в частности, навигационных приложений
· среднеквадратические ошибки оценок всех компонент вектора состояния минимальны;
· определитель и главные миноры ковариационной матрицы минимальны;
· след ковариационной матрицы, представляющий собой сумму вторых центральных моментов компонент вектора состояния динамической системы минимален;
· оценка любой линейной комбинации компонент вектора состояния имеет минимальную среднеквадратическую ошибку.
Рассмотрим теперь совместную плотность распределения 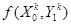, используемую для выработки оптимальной оценки. Известно, что эта плотность по правилу перемножения плотностей может быть представлена в виде
.
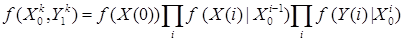Фрагменты этой плотности 
и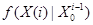 
при описании поведения динамической системы и процесса измерений уравнениями
,
,
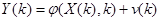где -вектор состояния размерности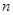 
; 
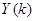-вектор измерений размерности 
; 
, 
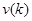-центрированные гауссовские векторы белошумных возмущений и ошибок измерений с ковариационными матрицам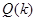и 
и 
соответственно, 
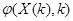-многомерная, в общем случае, нелинейная функция; 
-гауссовский вектор начальных условий,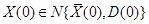 
,
в свою очередь, могут быть представлены с использованием плотностей распределения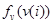 
и 
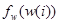как
,
.
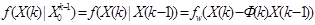Совместная плотность распределения 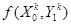при этом примет следующий вид:
.
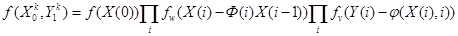Таким образом, имея совместную плотность распределения можно получить условную плотность распределения и решить задачу оптимального оценивания вектора 
с использованием выражения (**).
Показано, что в случае описания поведения динамической системы и процесса измерений линейными уравнениями при гауссовском распределении ошибок измерений и возмущений в рамках байесовского подхода может быть получены рекуррентные процедуры, получившие название линейного фильтра Калмана.
Фактически рассмотренная процедура является решением задачи оценивания в рамках байесовкого подхода когда используется совместная плотность распределения.
