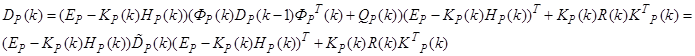- Дискретный фильтр Калмана предполагает использование марковской последовательности и проведения линейных измерений в дискретные моменты времени. Как следствие необходим расчет состояния динамической системы с использованием уравнений непрерывной динамической системы с вектором состояния, включающим вектор состояния собственно динамической системы, а также векторы состояния формирующих фильтров, используемых для описания возмущений и ошибок измерений, имеющих небелошумный характер. Как следствие, необходимо выполнение следующих типовых этапов.
1.1 Стохастическое описание небелошумных возмущений и ошибок измерений с использованием корреляционных функций или спектральных плотностей
1.2 Подбор формирующих фильтров вида
например, для корреляционной функции вида
формирующий фильтр имеет вид
, 
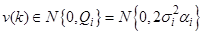
1.3 Стохастическое описание линейными дифференциальными уравнениями собственно динамической системы.
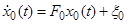
1.4 Формирование расширенного вектора состояния.
1.5 Описание поведения динамической системы матричными уравнениями с непрерывным временем в расширенном пространстве состояния.
где 
-матрица небелошумных возмущений, воздействующих на поведение собственно динамической системы.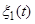 
-вектор возмущений формирующих фильтров.
1.6 Переход к описанию марковской последовательности в моменты проведения измерений и расчет эквивалентной ковариационной матрицы возмущений.
,
,
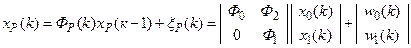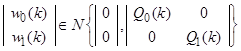при этом на этапе прогноза используются выражения фильтра Калмана для расширенного вектора состояния
,
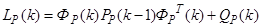
Применительно к модели измерений, если измерения не линейны, используется один из нелинейных субоптимальных фильтров калмановского типа, полагая, что линеаризация допустима.
Обработка измерений осуществляется в расширенном пространстве с
Настройкой на модель измерений
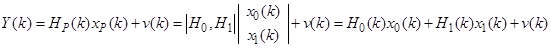
с использованием выражений
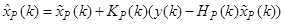
После выработки оценок на этапе обработки измерений в случае нелинейных измерений проводится гауссовская аппроксимация апостериорной плотности с параметрами 
.
Уравнение ошибок линейного фильтра, когда коэффициент фильтра отличен от оптимального
Предположим, что оценка линейного фильтра вырабатывается с использованием выражения
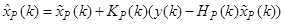
где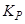 
-некоторый коэффициент усиления фильтра
В этом случае ошибка оценки фильтра может быть представлена как
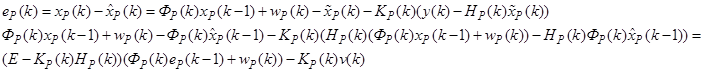
Определяя теперь действительную ковариационную матрицу ошибки оценки для независимых белошумных ошибок измерений и возмущений можно получить следующее выражение для ковариационной матрицы:
