Момент 
силы 
относительно какой-нибудь оси вращения определяется формулой
,
где l – расстояние от прямой, вдоль которой действует сила, до оси вращения.
Основной закон динамики вращательного движения (закон сохранения момента импульса) выражается уравнением
,
где - момент сил, приложенных к телу, 
- момент импульса тела,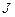 
- момент инерции тела, ω – его угловая скорость.
Твердое тело, находящееся под действием вращающего момента , движется с угловым ускорением
,
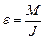где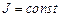 
- момент инерции тела относительно оси вращения.
Моменты инерции некоторых тел:
- тонкостенной круглой трубы (обруча) относительно оси совпадающей с осью трубы (обруча)
, 
- радиус трубы (обруча), - тонкого стержня длиной
относительно оси, перпендикулярной к стержню и проходящей сквозь его середину 
, - сплошного однородного круглого цилиндра (диска) относительно оси, совпадающей с его осью
, - сплошного однородного шара, относительно оси совпадающей с его диаметром
.
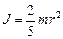Соотношение Штейнера:
,
где 
- момент инерции тела относительно оси, проходящей сквозь центр инерции, 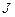- момент инерции относительно оси, параллельной первой, 
- расстояние между осями.
Кинетическая энергия вращающегося тела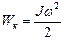 
.
146. Однородный цилиндр массы 
и радиуса 
вращается без трения вокруг горизонтальной оси под действием веса груза 
, прикрепленного к легкой нити, намотанной на цилиндр. Найти угол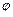 
поворота цилиндра в зависимости от времени, если при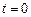 
.
147. Однородный сплошной шар радиусом R = 10 см и массой m = 5 кг вращается вокруг оси симметрии согласно уравнению 
(рад). Определите вращающий момент M в момент времени t = 3 c.
148. Однородный стержень длиной 
и массой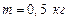 
вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня. С каким угловым ускорением 
вращается стержень, если на него действует момент сил 
?
149. Две гири с массам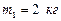и 
и 
соединены нитью, перекинутой через блок массой 
. Найти ускорение 
, с которым движутся гири, и силы натяжения 
и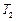 
нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.
150. Диск массой 
катится без скольжения по горизонтальной плоскости со скоростью 
. Найти кинетическую энергию диска.
151. Вентилятор вращается с частотой 
. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 
. Работа сил торможения 
. Найти момент инерции 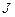вентилятора и момент сил торможения .
152. Груз, подвешенный на нити длиной 
, равномерно вращается по кругу в горизонтальной плоскости. Найти период обращения груза, если при его вращении нить отклонена от вертикали на угол 
.
153. Оценить, с какой минимальной скоростью 
нужно выпустить на экваторе Земли снаряд массы 
, чтобы изменить продолжительность земных суток на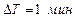 
?
154. Однородный диск радиуса  имеет круглый вырез как показано на рис. 8. Масса оставшейся (заштрихованной) части диска  . Найти момент инерции такого диска относительно, оси, проходящей через точку O и перпендикулярной к плоскости диска.
| 
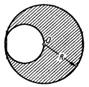Рисунок 8
|
155. Найти момент инерции диска, описанного в предыдущей задаче, относительно оси, проходящей через центр круглого выреза и перпендикулярной к плоскости рисунка.
Колебания
Колебания это повторяющийся в той или иной степени во времени процесс изменения состояний системы.
Уравнение гармонического колебательного движения имеет вид
,
где 
– смещение колеблющейся точки от положения равновесия,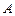 
– амплитуда, 
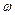– циклическая частота, 
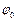– начальная фаза.
Циклическая частота связана с периодом колебаний соотношением
.
Период колебания (T) это время в течении которого система совершает одно полное колебание
· математический маятник 
, l – длина нити;
· физический маятник 
, b – расстояние от точки подвеса маятника до центра инерции, J – момент инерции маятника относительно оси проходящей через точку подвеса маятника;
· пружинный маятник 
, k – жесткость пружины.
При сложении двух одинаково направленных гармонических колебаний одинакового периода получается гармоническое колебание того же периода с амплитудой
,
,
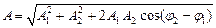где 
, 
- амплитуды слагаемых колебаний, 
, 
их начальные фазы.
При сложении двух взаимно перпендикулярных колебаний, одинакового периода, уравнение траектории результирующего колебания имеет вид
.
В случае затухающих колебаний смещении точки со временем подчиняется уравнению
,
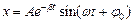где 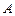- амплитуда колебаний в начальный момент времени.
Логарифмический декремент затухания
.
156. Материальная точка совершает гармонические колебания согласно уравнению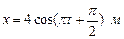 
. Определите: амплитуду, период, начальную фазу колебаний, максимальную скорость точки, максимальное ускорение точки. Через сколько времени после начала отсчета точка будет проходить через положение равновесия?
157. Определите максимальные значения скорости и ускорения точки, совершающей гармонические колебания с амплитудой 
и периодом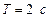 
.
158. Найти период колебания стержня, подвешенного так, что ось подвеса проходит через точку, находящуюся на расстоянии 
от одного из концов стержня. Масса стержня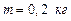 
, длина 
.
159. Найти период колебания диска, подвешенного так, что ось подвеса проходит через точку, находящуюся на расстоянии 
от центра диска. Масса диска 
, диаметр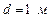 
.
160. Физический маятник, который представляет собой шар, радиус которого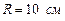 
подвешен на нити длиной 
. Определить во сколько раз мы ошибемся, если будем, рассчитывая период, такого маятника, считая его математическим с длиной 
.
161. Частица массой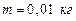 
совершает гармонические колебания с периодом 
. Полная энергия колеблющейся частицы 
. Определить амплитуду А колебаний и наибольшее значение силы Fmax, действующей на частицу.
162. Каков логарифмический декремент затухания маятника длиной 
, если его начальная амплитуда 10o, а через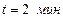 
амплитуда равна 0,3o.
163. Через сколько времени энергия колебаний камертона с частотой 
уменьшится в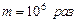 
, если логарифмический декремент затухания равен 
.
164. Складываются два колебания одинакового направления, выраженные уравнениями 
и 
где 
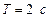. Построить векторную диаграмму сложения этих колебаний и написать уравнение результирующего колебания.
165. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, уравнения которых 
и 
, где 
, 
, 
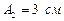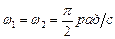. Написать уравнение траектории и построить ее. Показать направление движения точки.
166. Складывается два колебания одинакового направления и одинакового периода: 
и 
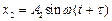, где 
, , 
, 
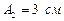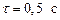. Определить амплитуду и начальную фазу результирующего колебания. Написать его уравнение. Построить векторную диаграмму для момента времени t = 0.
167. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых: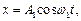 
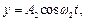где 
, 
, 
. Найти уравнение траектории точки. Построить траекторию с соблюдением масштаба и указать направление движения точки.
