Функции и отображения


 Отношение F X Y называется отображением X в Y или функцией, определен- ной в X и принимающей значения в Y, если для x:
Отношение F X Y называется отображением X в Y или функцией, определен- ной в X и принимающей значения в Y, если для x:
x, y 1
F x, y 2
F y 1
y 2.
 Если x, y F, то элемент y называется значением F в x и обозначается как
Если x, y F, то элемент y называется значением F в x и обозначается как
y  F x.
F x.
Используются также обозначения:
 F: X Y,
F: X Y,
 F: x F x.
F: x F x.
Принципиально важным свойством отображения является то, что любому значе- нию "аргумента" x ставится в соответствие единственный элемент y. Такое понятие, как "многозначная" функция, здесь не рассматривается. Вполне правомерно, ко- нечно, определить отображение, значениями которого являются подмножества не- которого данного множества, состоящие более чем из одного элемента. Но такое определение практически бесполезно, т. к. не удается разумным образом опреде- лить алгебраические операции над значениями таких функций. Например, операция

 извлечения корня из вещественного числа z приводит к двум значениям со зна-
извлечения корня из вещественного числа z приводит к двум значениям со зна-
ками "плюс" и "минус". Но тогда как понимать равенство:
z z 2
z? Левая
часть имеет три разных значения, а правая — только два. (Хотя, конечно, сущест- вует и понятие Римановой поверхности.)
Сделаем еще одно замечание. Обычно (в "школьной" математике) различают понятия функции и ее графика. В данном выше определении эти понятия со- впадают.
В современной математике важнейшую роль играет рассмотрение отображения (функции) как единого объекта (такого же, как точка или число) и проведение яс- ного различия между отображением F и любым из его значений F x. Первое есть
 элемент множества отображений X в Y, обозначаемого как X Y, второе — элемент множества Y, причем
элемент множества отображений X в Y, обозначаемого как X Y, второе — элемент множества Y, причем
 F x, y X Y / y F x.
F x, y X Y / y F x.
Таким образом, отображение F есть некоторое множество упорядоченных пар x, y.
Пусть
F: X Y. Пусть также
A X. Тогда множество


 F A y Y / x A y F x
F A y Y / x A y F x

 называется образом множества А при отображении F. Здесь — квантор сущест- вования. x читается: существует х. Прообразом множества B Y при отображе- нии F называется множество
называется образом множества А при отображении F. Здесь — квантор сущест- вования. x читается: существует х. Прообразом множества B Y при отображе- нии F называется множество


 F 1 B x X / F x B.
F 1 B x X / F x B.
Пусть
F: X Y. Пусть
A X. Тогда множество
 F (A Y) A Y
F (A Y) A Y
называется сужением отображения F на множестве А.
Линейные пространства
Часто приходится встречаться с объектами, над которыми производятся операции сложения и умножения на числа. Например, векторы в геометрии в трехмерном пространстве умножаются на числа и складываются. Вещественные функции веще- ственных аргументов умножаются на числа и складываются и т. п. Одни и те же операции производятся над совершенно разными объектами. Для того чтобы изу- чить все такие примеры с единой точки зрения, вводится понятие линейного (или векторного) пространства.
Пусть на множестве L элементов
x, y, z,... заданы два отображения:
 L L L,
L L L,
L R L,
где R — множество действительных чисел ("вещественная прямая"). Обозначим эти отображения как:
соответственно.
x, y x y L,

 x, x L
x, x L
Тогда множество L называется действительным линейным пространством, если для введенных отображений выполнены следующие требования:
1.  x y y x (коммутативность).
x y y x (коммутативность).
2. 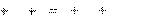 x y z x y z (ассоциативность).
x y z x y z (ассоциативность).
3.  L: x L x x (существование нуля).
L: x L x x (существование нуля).
4.  Для x L x L x x (существование противоположного элемен- та).
Для x L x L x x (существование противоположного элемен- та).
5.  1 x x 1 R.
1 x x 1 R.
6. 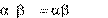 x x.
x x.
7.  x x x.
x x x.
8.  x y x y.
x y x y.
Часто говорят о линейном векторном пространстве. Сами элементы L также назы- ваются векторами.
Если вместо множества R действительных чисел используется множество C ком- плексных чисел, то получим комплексное линейное пространство.
Непустое подмножество линейного пространства L называется подпространством, если оно само является линейным пространством по отношению к определенным в L операциям.

 Пусть x — произвольное непустое семейство элементов линейного пространст- ва L (счетность множества x не предполагается). Определение понятия семейства элементов было дано выше. Рассмотрим все подпространства линейного пространст-
Пусть x — произвольное непустое семейство элементов линейного пространст- ва L (счетность множества x не предполагается). Определение понятия семейства элементов было дано выше. Рассмотрим все подпространства линейного пространст-
 ва L, содержащие заданную систему векторов x. Пересечение этих подпро-
ва L, содержащие заданную систему векторов x. Пересечение этих подпро-
странств, очевидно, тоже будет подпространством. Это так называемое наименьшее


 подпространство, содержащее x. Оно называется подпространством, порожден- ным множеством x, или линейной оболочкой семейства элементов x.
подпространство, содержащее x. Оно называется подпространством, порожден- ным множеством x, или линейной оболочкой семейства элементов x.
Примеры линейных пространств.
1. Множество R действительных чисел с обычными операциями сложения и умно- жения (L совпадает с R).
2. Совокупность систем n действительных (или комплексных) чисел
 x x 1, x 2,..., xn
x x 1, x 2,..., xn
, где сложение и умножение на число определяются формулами
 x y x 1
x y x 1
y 1, x 2
y 2,..., xn
yn,
x x 1,
x 2,...,
xn.
называется n -мерным арифметическим пространством и обозначается Rn
действительного пространства) или Cn (в комплексном случае).
(для
3. Множество непрерывных на отрезке a, b функций с обычными операциями
сложения и умножения на числа образует векторные пространства C a, b,
C 2 a, b.
Конечное множество векторов xi
называется линейно зависимым, если существует
 множество чисел i, из которых не все равны нулю, такое, что
множество чисел i, из которых не все равны нулю, такое, что
i xi
0. Если

 i xi 0 i: i 0,
i xi 0 i: i 0,
то конечное множество xi
называется линейно независимым.
Замечание. Важно, что линейная зависимость и линейная независимость — свой- ства множества векторов. Однако соответствующие прилагательные часто условно применяются к самим векторам, которые называются линейно зависимыми или ли- нейно независимыми.
 Множество X (не обязательно конечное) называется линейно независимым, если линейно независимо любое его конечное подмножество. В противном случае мно- жество X — линейно зависимо.
Множество X (не обязательно конечное) называется линейно независимым, если линейно независимо любое его конечное подмножество. В противном случае мно- жество X — линейно зависимо.
Если
xi — конечное множество и для некоторого x L справедливо представле-
ние x
ixi, то говорят, что x является линейной комбинацией векторов
xi.
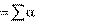
 Линейное пространство L называется конечномерным, если в нем существует n ли-
Линейное пространство L называется конечномерным, если в нем существует n ли-
нейно независимых векторов, а любые n 1 векторы — линейно зависимы. В этом
случае говорят, что L имеет размерность n. Любой набор из n линейно независи- мых векторов n -мерного пространства L называется базисом этого пространства. Если существует любое количество линейно независимых векторов, то пространст- во L называется бесконечномерным. Понятие базиса бесконечномерного простран- ства здесь не обсуждается.
Примеры.
1. Можно доказать, что пространства
Rn, Cn
имеют размерность n, поэтому и бы-
ли названы ранее n -мерными пространствами.
2. Пространства C a, b, C 2
a, b бесконечномерны.
3. Базисом в пространстве от нуля.
4. Базис в пространстве Rn
R 1 является любое действительное число, отличное
образует, например, система векторов 1, 0,..., 0,
0, 1,..., 0,..., 0, 0,..., 1.
n -мерные пространства изучаются в курсах по линейной алгебре и являются осно- вой для задач нелинейного программирования. Пространства с бесконечным чис- лом измерений изучаются в функциональном анализе и представляют основной интерес для бесконечномерных оптимизационных задач, например, для задач тео- рии оптимального управления.
Нормированные пространства
В теории метрических пространств сформулировано понятие расстояния между элементами произвольного множества. В этом смысле метрические пространства являются частным случаем более общих топологических пространств. Концепция же линейных пространств позволяет наделить множество некоторой алгебраиче- ской структурой с помощью определения операций сложения элементов и умноже- ния их на числа. Нормированные пространства являются одновременно линейными и метрическими пространствами и относятся к важному классу топологических ли- нейных пространств. Развитие теории нормированных пространств связано с име- нем Стефана Банаха и целого ряда других авторов. Структура нормированных про- странств оказывается чрезвычайно удобной для изучения основных конструкций теории оптимизации в достаточно общем виде.
Банаховы пространства

 Линейное пространство L называется нормированным, если на L задан функционал
Линейное пространство L называется нормированным, если на L задан функционал
f: L R, удовлетворяющий следующим четырем условиям для x, y L, R:
1. f x
2. f x
0.

 0 x 0.
0 x 0.
3. 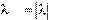 f x f x.
f x f x.
4.  f x y f x f y (неравенство треугольника).
f x y f x f y (неравенство треугольника).
 Такой функционал f называется нормой в L. Значение f x обозначается
Такой функционал f называется нормой в L. Значение f x обозначается  x
x  и на- зывается нормой элемента x. Нормированным пространством называется линей- ное пространство L с заданной в нем нормой.
и на- зывается нормой элемента x. Нормированным пространством называется линей- ное пространство L с заданной в нем нормой.
 Если x x — норма в L, то функционал L L R вида
Если x x — норма в L, то функционал L L R вида
d x,
y x y есть
расстояние в L. Норма индуцирует соответствующую метрику. Справедливость ак- сиом метрики легко проверяется.
Таким образом, для нормированных пространств имеют смысл все понятия, вве- денные для метрических пространств. Полное нормированное пространство назы- вается банаховым пространством или B -пространством.
 Пример 1. В пространстве мулой:
Пример 1. В пространстве мулой:
C a, b непрерывных функций определим норму фор-

 f max
f max
t a, b
f t.
Порожденная этой нормой метрика совпадает с ранее рассматриваемой метрикой для этого множества. Как мы указывали, это множество функций является полным относительно своей метрики, и, следовательно, пространство C a, b является ба-
наховым пространством.
Подпространством нормированного пространства L называется подпространство линейного пространства L (линейное подпространство), которое является замкну- тым множеством относительно расстояния, индуцированного заданной нормой. Иначе говоря, подпространство нормированного пространства есть линейное под- пространство, содержащее все свои предельные точки. Еще раз отметим, что толь- ко замкнутые линейные подпространства нормированного пространства будут на- зываться подпространствами нормированного пространства.
Например, в пространстве C a, b непрерывных функций с указанной нормой
многочлены образуют подпространство соответствующего линейного пространст- ва, но не замкнутое. Следовательно, это подпространство не будет подпространст- вом нормированного пространства C a, b. В конечномерном нормированном про-
странстве ситуация проще. Там любое линейное подпространство обязательно замкнуто.
 Совокупность элементов (не обязательно замкнутую), содержащую вместе с x, y их произвольную линейную комбинацию x y (подпространство линейного простран- ства), будем в случае нормированных пространств называть линейным многообразием.
Совокупность элементов (не обязательно замкнутую), содержащую вместе с x, y их произвольную линейную комбинацию x y (подпространство линейного простран- ства), будем в случае нормированных пространств называть линейным многообразием.
Для нормированных пространств, являющихся частным случаем линейных про- странств, сохраняются все определения и результаты, полученные для линейных пространств. Например, такие понятия, как наименьшее подпространство, порож- денное подпространство, линейная оболочка и т. д.
 В теории нормированных пространств замыкание линейной оболочки произволь- ного непустого множества x называется подпространством, порожденным эле-
В теории нормированных пространств замыкание линейной оболочки произволь- ного непустого множества x называется подпространством, порожденным эле-
 ментами x. (Можно доказать, что указанное замыкание действительно будет линейным подпространством.)
ментами x. (Можно доказать, что указанное замыкание действительно будет линейным подпространством.)
 Система элементов x нормированного пространства L называется полной, если по-
Система элементов x нормированного пространства L называется полной, если по-
рождаемое ею линейное многообразие имеет замыкание, совпадающее со всем про- странством L. Иначе говоря, если порождаемое ею подпространство совпадает с L.
Пример 2. Система функций 1, t, t 2, t 3,..., tn,... полна в пространстве непрерыв- ных функций C a, b.
Евклидовы пространства
В евклидовых пространствах вводится понятие скалярного произведения, а уже на его основе определяется норма.
 Пусть в действительном линейном пространстве L задан функционал L L R. Значение этого функционала называется скалярным произведением и обозначается
Пусть в действительном линейном пространстве L задан функционал L L R. Значение этого функционала называется скалярным произведением и обозначается
x, y,
x L,
y L, если выполняются следующие условия:
1.  x L:
x L:
2.  x, x
x, x
x, x 0.
0 x 0.
3. 
 x, y x, y, R.
x, y x, y, R.
4. x 1
x 2,
y x 1,
y x 2, y.
5.  x, y y, x.
x, y y, x.
Линейное пространство с заданным в нем скалярным произведением называется евклидовым пространством. Иногда евклидовы пространства называются предгиль- бертовыми пространствами, а для скалярного произведения используется обозна-
чение  y.
y.
Норма в евклидовом пространстве вводится формулой

 x x, x.
x x, x.
Можно проверить, что все аксиомы нормы оказываются при этом выполненными. В евклидовом пространстве может быть задан угол между векторами. Для ненуле-
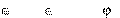 вых векторов x L, y L угол определяется выражением
вых векторов x L, y L угол определяется выражением
cos
x, y.
 x y
x y

 Можно доказать, что, как и должно быть, правая часть равенства не превосходит единицы.
Можно доказать, что, как и должно быть, правая часть равенства не превосходит единицы.
Если для ненулевых векторов
x L,
y L имеем
x, y
0, то /2, а векторы
x и y называются ортогональными.
 Система ненулевых векторов x из L называется ортогональной, если они попар- но ортогональны:
Система ненулевых векторов x из L называется ортогональной, если они попар- но ортогональны:
 x, x 0.
x, x 0.
 Счетность множества x не предполагается.
Счетность множества x не предполагается.
Упражнение 1. 6
Доказать, что если векторы xα
ортогональны, то они линейно независимы.

 Если система векторов (семейство элементов) x ортогональна и полна в L, то она называется ортогональным базисом пространства L. Если при этом
Если система векторов (семейство элементов) x ортогональна и полна в L, то она называется ортогональным базисом пространства L. Если при этом
: x 1, то имеем ортогональный нормированный базис или ортонормальный

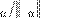 базис. Если x — ортогональная система, то x x — ортонормальная.
базис. Если x — ортогональная система, то x x — ортонормальная.
Примеры евклидовых пространств.
1. Пространство действительных чисел R. Скалярное произведение — обычное произведение действительных чисел.
2. Rn
— n - мерное арифметическое пространство с элементами вида
 x x 1, x 2,..., xn
x x 1, x 2,..., xn
, где
xi — действительные числа. Операции сложения и ум-
ножения на числа — общеизвестны, а скалярное произведение задается соотно-
 n
n
шением x, y xiyi.
i 1
3. Линейное пространство C 2
a, b непрерывных на
a, b действительных функ-
ций со скалярным произведением
 b
b
f, g f t g t dt
a
является евклидовым пространством. Можно установить, что все аксиомы ска- лярного произведения оказываются выполненными.
В этом случае норма, очевидно, задается выражением
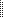
 f 2 f, f
f 2 f, f
b
 f t 2 dt.
f t 2 dt.
a
Индуцированная этой нормой метрика имеет вид
d f, g f g
b
f t g t
a
2 dt
1/2
 ,
,
что совпадает с ранее введенной метрикой при наделении данного множества
функций структурой метрического пространства и выборе обозначения C 2
a, b.
Одним из ортогональных базисов пространства C 2
рическая система функций:
a, b является тригономет-

 1 2, cos n 2 t, sin n 2 t n 1, 2,....
1 2, cos n 2 t, sin n 2 t n 1, 2,....
b a b a
4. Ранее рассматривалось также метрическое пространство C 2
a, b с метрикой
d f, g
 Норма определялась формулой
Норма определялась формулой
max
 t a, b
t a, b
f t g t.
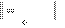
 f max
f max
t a, b
f t.
(Было установлено, что это банахово пространство.)
Поставим вопрос, можно ли наделить данное нормированное пространство структурой евклидова пространства. Для этого достаточно задать вышеприве- денную норму с помощью некоторого скалярного произведения:

 x x, x.
x x, x.
Можно показать, что ответ будет отрицательным. Норму пространства C a, b нель-
зя задать с помощью скалярного произведения. Таким образом, не все нормирован- ные пространства можно "превратить" в евклидовы пространства. Евклидовы про- странства составляют лишь часть нормированных пространств. Еще раз отметим, что
пространство C a, b дает пример банахова, но не евклидова пространства.
Можно доказать следующее утверждение (характеристическое свойство евклидо- вых пространств).
 Теорема 1.8. Для того чтобы нормированное пространство L было евклидовым,
Теорема 1.8. Для того чтобы нормированное пространство L было евклидовым,
необходимо и достаточно, чтобы для x, y L выполнялось равенство

 x y 2
x y 2
Доказательство опускаем.
x y 2
2 x 2
y 2.
Теорема 1.9 (процесс ортогонализации Шмидта). Пусть
f 1,
f 2,...,
fn,...
есть линейно независимая (счетная) система векторов в евклидовом пространстве
 L. (Ясно, что в эту систему не могут входить нулевые векторы, иначе получим ли- нейную зависимость). Тогда в L существует система векторов
L. (Ясно, что в эту систему не могут входить нулевые векторы, иначе получим ли- нейную зависимость). Тогда в L существует система векторов
Такая, что:
1.  i — ортонормальна.
i — ортонормальна.
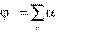
 n
n
1, 2,...,
n,...,
2. n nifi, причем nn 0.
i 1
(Переход от линейно независимой системы векторов к ортогональной называет- ся процессом ортогонализации.)
 Доказательство. Положим
Доказательство. Положим
| 1 f 1, n fn 1, i n n 1 fn 1 2 i fn 1 i fi. i 1 i i 1 | (1.3) |
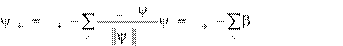
 В этом случае вектор вительно,
В этом случае вектор вительно,
n 1 будет ортогонален всем векторам
i, i
1,..., n. Дейст-
Для n
1  имеем
имеем
n 1,
j fn 1, j
n fn 1, i

 2
2
i 1 i
i, j.
2 f 2
f 2, 1
 2 1.
2 1.

 Но 1
Но 1
f 1, поэтому
2 f 2
f 2, f 1 f 1
, f,
f 2, f 1 f,
f, f
f 2, f 1
f 2 0.
 1 2 2 1
1 2 2 1
2 1 1 2 1 2 1
f f
1 1
 Установлена ортогональность 1 и 2. Покажем по индукции, что система векто-
Установлена ортогональность 1 и 2. Покажем по индукции, что система векто-
 ров 1,..., n,..., построенная согласно выражению (1.3), ортогональна.
ров 1,..., n,..., построенная согласно выражению (1.3), ортогональна.

 Пусть 1,..., n уже построены и ортогональны. Покажем, что тогда вектор n 1
Пусть 1,..., n уже построены и ортогональны. Покажем, что тогда вектор n 1
будет ортогонален всем
i, i
1,..., n.
 Имеем (для любого фиксированного j 1,..., n:
Имеем (для любого фиксированного j 1,..., n:
n 1,
j fn 1, j
n fn 1, i
 2
2
i 1 i
i, j
fn 1, j
fn 1, j
 2
2
j
j, j 0.
(Очевидно, в данном выражении только одно слагаемое суммы не равно нулю,


 а именно слагаемое с индексом i j. Остальные слагаемые равны нулю, т. к. i,
а именно слагаемое с индексом i j. Остальные слагаемые равны нулю, т. к. i,
 i 1,..., n ортогональны и
i 1,..., n ортогональны и
i, j
0, i j.)
Последнее соотношение может выполняться и если в результате процедуры (1.3) будут все время получаться нулевые векторы. Покажем, что это невозможно из-за
линейной независимости системы векторов
f 1,
f 2,...,
fn,...
Действительно, пусть
получили
n 1 0, тогда
 f
f
n fn 1, i n f,
 n 1 2
n 1 2
i i i
i 1 i i 1
что противоречит линейной независимости
f 1,
f 2,...,
fn,...
Следовательно
 n 1 0. Для окончательного доказательства теоремы достаточно положить
n 1 0. Для окончательного доказательства теоремы достаточно положить
Теорема доказана.
n n.
 n
n






