Основные представления молекулярной физики. Термодирамика

ЛЕКЦИЯ 6

Молекулярная физика изучает те свойства вещества, которые обусловлены его молекулярным строением.Понятно, что теоретическое изучение молекулярных систем связано с большими трудностями. Если предположить, что движение молекул является чисто механическим и подчиняется законам классической механики, то для полного описания всей молекулярной системы нужно решить механическую задачу о движении всех молекул под действием заданных сил. Это значит, что должны быть записаны и решены уравнения движения, число которых равно числу молекул в данной системе. Но число молекул настолько велико, что не только решить, но даже написать такое чудовищное число уравнений невозможно.

Однако именно грандиозность числа молекул делает ненужным рассмотрение каждой из них в отдельности. При таком большом числе частиц оказывается возможным ограничиться знанием лишь средних величин, характеризующих их движение: их средней скорости, средней энергии и т.д. Метод, применяемый для объяснения макроскопических свойств тел с точки зрения их молекулярного строения, представляет собой статистический метод. Этот метод лежит в основе молекулярно-кинетической теории вещества.

Возможен и другой способ описания тепловых явлений, не требующий детального рассмотрения тех процессов, которые при этом происходят. В основе этого метода лежит небольшое число фундаментальных законов, установленных путем обобщения очень большого количества опытных данных. Такое описание возможно, благодаря введению понятия об энергии, ее превращениях и способах передачи и установлению тех основных законов, которым подчиняются эти превращения энергии из одних видов в другие (термодинамический метод). Раздел физики, рассматривающий процессы с указанной энергетической точки зрения, носит название термодинамики.

Понятие состояния вещества. Идеальный газ. Изучая в курсе механики законы, управляющие движением тел, мы не интересовались, каким образом устроены эти тела, какими свойствами они обладают.

С точки зрения современных представлений, все вещества состоят из молекул (атомов). Молекула – это наименьшая частица вещества, сохраняющая все его химические свойства. Размеры молекул и атомов чрезвычайно малы, порядка 10^{-8 см. Зато число частиц необычайно высоко. В одном грамме воды, например, содержится 3,3∙1022} молекул.

Между молекулами в веществе действуют силы притяжения и отталкивания, зависящие от расстояния между частицами. На существование межмолекулярных сил указывает, в частности, существование трех агрегатных состояний вещества – твердого, жидкого и газообразного. В твердом и жидком состоянии молекулы притягиваются друг к другу настолько, что тела сохраняют свой объем, а в случае твердого тела – еще и форму. В газообразном же состоянии взаимодействия значительно слабее, так что газ заполняет весь предоставленный ему объем, как бы велик он ни был.

Таким образом, различные состояния вещества отличаются по своим свойствам в силу различия их межмолекулярного взаимодействия.

Способность газа распространяться по всему объему сосуда, в котором он заключен, показывает, что молекулы газа находятся в постоянном движении. Ряд свойств газа показывает также, что эти движения молекул отличаются полной беспорядочностью, хаотичностью. Это значит, что не существует какого-либо направления для движения частиц, которое было бы преимущественным сравнительно с другими. Это хаотическое движение молекул носит название теплового движения.

Все молекулы газа движутся беспорядочно и испытывают упругие столкновения друг с другом и со стенками.

Состояние определенной массы газа определяется следующими тремя величинами: давлением Р, под которым находится газ, его температурой Т и занимаемым им объемом V. Эти три величины называются параметрами состояния газа.

Давлением газа Р называется сила F, отнесенная к единице площади S поверхности стенки, нормальной к этой силе:

Свойство газа оказывать давление на стенки содержащего его сосуда – одно из основных свойств газа. Размерность давления есть размерность силы, деленной на размерность площади: [ Р ] = Н/м² = Па (Паскаль).

Под объемом идеального газа понимают геометрический объем сосуда, в котором газ находится.

Из опыта известно, что если привести в соприкосновение два тела с разными температурами, то со временем их температуры станут одинаковыми – между телами установится тепловое равновесие. Если приложить руки к этим телам, обе руки будут испытывать совершенно одинаковые ощущения.

Таким образом, температура – это величина, характеризующая тепловое равновесие: у тел, находящихся в тепловом равновесии температуры одинаковы. Физическое определение температуры должно основываться на такой физической величине, характеризующей состояние тела, которая была бы автоматически одинаковой у любых двух тел, находящихся в тепловом равновесии друг с другом. Таким замечательным свойством обладает средняя кинетическая энергия поступательного движения молекул газа. Принято определять температуру величиной , пропорциональной 2/3 от этой энергии:

Здесь m – масса, – скорость молекулы, а угловые скобки означают, что должно быть взято среднее значение выражения, стоящего в скобках. Поскольку кинетическая энергия есть величина положительная, то положительна и температура .

Удобной условной единицей измерения температуры – градусом. Градус определяется как одна сотая разности между температурами таяния льда и кипения воды при нормальном атмосферном давлении.

Параметры состояния газа Р, Т, V и М описывают состояния всего газа в целом и называются макроскопическими параметрами. Движение каждой молекулы определяется ее координатами, скоростью, кинетической энергией и т.п., то есть микроскопическими параметрами.

Перечисленные три величины Р, Т и V не являются независимыми. Каждая из них является функцией двух других Уравнение, связывающее параметры состояния называется уравнением состояния и может быть записано в общем виде так:

Если уравнение состояния известно в явном виде, то любой параметр можно вычислить, зная остальные.

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева), полученное в результате обобщения опытных данных, имеет вид:

, (1)

где M – масса газа, а − молярная масса газа; постоянная величина = 8,31 Дж/(моль·К) называется универсальной газовой постоянной. Величина представляет число молей данного газа, заключенных в объеме .

Вывод основного уравнения молекулярно-кинетической теории. Первые существенные успехи были достигнуты молекулярно-кинетической теорией в объяснении свойств идеальных газов.

Существование давления в газах с точки зрения молекулярно-кинетической теории связано с тем, что молекулы газа, сталкиваясь со стенками сосуда, передают им некоторый импульс.

Представим себе прямоугольный сосуд, в котором находится некоторое число N молекул идеального газа. Стенки сосуда будем считать идеально отражающими, т.е. примем, что при отражении от стенки скорость молекулы не изменяется по величине. В силу хаотичности движений молекул газа следует предположить, что молекулы движутся с разными скоростями. Пусть молекул имеют скорость , молекул − скорость , молекул − скорость 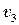и т.д.

Если молекула, скорость которой равна , ударяется о стенку, расположенную перпендикулярно оси x, то после отражения ее скорость будет равна (рис. 1.)

Как видно из рис.1, после отражения от стенки изменится только х- ая составляющая скорости молекулы, у- ая составляющая останется прежней.

Следовательно, изменение импульса данной молекулы в направлении оси x равно:

Долетев до противоположной стенки, молекула отразится от нее и снова ударится о первую стенку. Конечно, рассматриваемая молекула на своем пути может испытать большее или меньшее число соударений с другими молекулами. Для последующего это не существенно, так как соударения происходят по закону упругих шаров, а при таких соударениях молекулы лишь обмениваются скоростями. Время между ударами молекулы об эту стенку, очевидно, составит

а число ударов молекулы за 1 с, соответственно, . За 1 с N_i молекул сообщат стенке импульс с компонентой вдоль оси х, равной

Импульс, передаваемый за единицу времени этими молекулами стенке, равен силе, с которой они действуют на стенку:

Сила, действующая на стенку, перпендикулярную оси x, со стороны всех N молекул, находящихся в сосуде, составит

(2)

Перепишем последнее соотношение в виде:

Величина есть среднее значение квадрата компоненты скорости в направлении оси х, поэтому

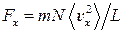Если эту силу разделить на площадь стенки S, то получим давление:

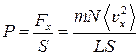Но LS = V, где V – объем сосуда и, следовательно,

. (3)

Воспользуемся теперь выражением . Усредняя его по всем молекулам, получим . Все направления движения молекул в сосуде равноценны. Поэтому 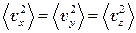и, следовательно, 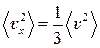. Тогда выражение (3) для давления принимает вид

(4)

или

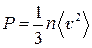Здесь n − концентрация молекул газа, т.е. число молекул в единице объема.

Учитывая, что равно средней кинетической энергии поступательного движения молекул , соотношение (4) можно записать следующим образом:

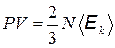. (5)

(6)

Это соотношение является одной из основных формул кинетической теории газов.

Выведенное соотношение (5) связывает давление газа со средней кинетической энергией поступательного движения молекул. Последняя величина пропорциональна абсолютной температуре газа, и поэтому, объединяя формулы (3) и (2), находим выражение

. (7)

Уравнение(7) представляет собой основное уравнение молекулярно-кинетической теории идеального газа. По закону, установленному Авогадро, в одинаковых объемах разных газов при одинаковых давлениях и температурах содержится одинаковое число молекул . Число молекул N в объеме газа можно записать в виде

где – число молей данного газа (М − масса газа, m − его молярная масса, в СИ имеющая размерность ), а N_A – число Авогадро, равное 6,023·10²³ моль^-1. В этих обозначениях уравнение состояния принимает вид:

, (8)

и совпадает, таким образом, с уравнением Клапейрона−Менделеева (1). Видим, что универсальная газовая постоянная R = kN_A, где k − постоянная Больцмана. Подставляя для k и N_A их значения, находим, как и следовало ожидать, R = 8,314 Дж/(К×моль).