Жоғарыда айтылғандай, қазіргі уақытта комьютерлік есептеулер мен модельдеу мүмкіндіктеріне байланысты механиканың есептерін шешу үшін, әрі қарайғы есептеулер мен модельдеу үшін әмбебаптылық және алгоритмдеу қасиеттеріне ие болатын аналитикалық әдістер біршама ыңғайлы болып табылады. Күрделі механикалық жүйенің матрицалық сипаттамалырна негізделген кинематикалық көрсеткіштерге (3.3-3.5) тәуелділіктер динамиканың есептерін шешу үшін матрицалық әдістерді қолдануға мүмкіндік береді. Есептеулер жағынан Ньютон-Эйлер теңдеулерінің көмегімен динамиканы сипаттау әдісі біршама тиімді болып табылады. Осы теңдеулердің қорытындысы Д¢Аламбер қағидасына негізделеді.
Сәйкесінше i-1, i буындарымен байланысқан, координаталар жүйесінің басы болып табылатын
Oi-1, Oi нүктелерінің орны қозғалмайтын координаталар жүйесіне қатысты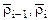 
радиус-векторларымен анықталатын 19-суретте есептеу сұлбасы берілген. 
радиус-векторы базалық санақ жүйесіндегі i-нші буынның массалар центрінің Si орнын анықтайды. 
векторлары сәйкесінше i-1 координаталар жүйесімен салыстырғандағы i- нші координаталар жүйесі басының орнын сипаттайды, сонымен қатар, сәйкесінше i-1 және i- нші координаталар жүйесіне қатысты массалар центрінің орнын Si анықтайды. Oi-1 нүктесінде i-1 буынынан i- нші буынға әсерінен 
реакция күші салынған. 
арқылы i-1 буынның реакция күштерінен моменттердің i- нші буынға әсер ететін бас вектор бенлгіленген.
19-сурет. Есептеу сұлбасы
Si массалар центрінде ауырлық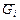 
салынған. i+1 –нші буынға i -нші буын жағынан 
қосынды күші және 
күш моменті әсер етсін. Сонда, Ньютонның 3-нші заңына сәйкес i -нші буынға i+1 –нші буын жағынан (- )-ге тең күш және 
тең момент әсер етеді.
Ньютонның заңына сәйкес, массалар центрінің қозғалысы туралы теоремаға сәйкес i -нші буын үшін
, (5.9)
мұндағы mi, asi - i -нші буынның массасы және массалар центрінің үдеуі.
Кинетикалық моменттің өзгеруі туралы Эйлер теоремасына сәйкес i -нші буын үшін жазылған, қозғалмайтын Si нүктесіне қатысты келесі түрдегі векторлық қатынас орындалады:
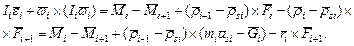(5.10)
Мұндағы Ii - i - нші дененің базалық координаталар жүйесіндегі Si нүктесіндегі инерция матрицасы. Бұл матрица инерция тензорына (5.3) сырттай ұқсас, бірақ та (5.3,а) өрнегіне базалық координаталар жүйесіндегі mk массасының координаталары кіреді. (5.10) өрнек рекурренттік түрде төмендегі түрде берілуі мүмкін:
,
(5.11)
(5.11) теңдігі алдыңғы кезеңдегі есептеулер нәтижесінде алынған 
мәндері кезінде соңғы буыннан бастап моменттер мен күштерді есептеуге мүмкіндік береді. Күш есебін осы жағдайда 
сырттан әсер ететін күшке тең деп есептей отырып, соңғы буынның есебінен бастайды.
Бірақ, егер кинетостатикалық есептің келтірілген әдісіне сүйенсек, онда (5.11) теңдік үлкен есептеулерді жүргізуді талап ететініне байланысты қиыншылықтар туады. Шындығындада, қозғалмайтын санақ жүйесіне қатысты i -нші буынның өзгеруі кезінде (5.11) теңдіктегі инерция матрицасының Ii элементтерінің мәні өзгереді. Бұл буын орнының әрбір өзгеруі кезінде инерция тензорының Ii элементтерінің қосымша есептеулерін жүргізуді талап етеді. Сондықтан да, (5.11) теңдікке кіретін шамалар олардың мәндері арқылы i - нші буынмен байланысқан төңіректік координаталар жүйесінде өрнектеледі.
