Принцип наименьших квадратов позволяет найти наилучшую модель идентификации для исследуемой экспериментальной выборки с заданным уравнением регрессии вида
 .
.
Если имеются достаточно веские основания для выбора формы этого уравнения, никаких проблем не возникает. Однако, в большинстве случаев конкретная форма модели заранее неизвестна и может, вообще говоря, быть различной.
На первый взгляд может показаться, что более сложная модель (увеличение степени полинома) всегда обеспечивает получение бóльшей точности. На самом деле это не так. При переходе к полиномам более высокой степени можно, конечно, получить лучшее согласие регрессионной кривой с экспериментальными данными. Для m = n это согласие будет абсолютным, но при этом получится худшее согласие с истинным характером процесса W (x). Дело в том, что экспериментальные данные представляют собой случайные величины и содержат лишь ограниченную информацию о характере W (x). Увеличение степени полинома целесообразно лишь до тех пор, пока из экспериментальной выборки извлекается надежная информация. Таким образом, возникает проблема выбора формы модели.
Подход к решению этой проблемы основан на статистическом исследовании уравнений регрессии.
1) Метод всех возможных регрессий основан на последовательном изучении всех возможных моделей (m < n), из которых отбирается лучшая модель.
Метод представляется мало пригодным для анализа сложных систем, так как отличается высокой трудоемкостью.
2) Метод исключения предполагает исследование наиболее полной (в пределах разумного) модели и последовательную проверку на значимость всех ее членов. При этом для каждого из членов модели вычисляется величина критерия Фишера F. На основе полученного множества { Fi } выбирается член уравнения регрессии, соответствующий минимальному значению критерия Fi. Если это минимальное значение меньше критического при выбранном уровне риска (Fi < F кр a), то соответствующий член исключается из регрессионного уравнения как несущественный, после чего все коэффициенты регрессии пересчитываются заново и вновь осуществляется проверка их значимости.
Если Fi > F кр a, то все члены модели существенны и уравнение регрессии остается в первоначальном виде. Однако, если это произошло уже на первом шаге исследования, стóит рассмотреть целесообразность усложнения первоначальной модели.
Трудоемкость этого метода меньше, чем метода всех возможных регрессий.
3) Метод включений по существу противоположен методу исключений и предусматривает последовательное включение в модель новых членов с проверкой их статистической значимости.
Трудоемкость этого метода существенно меньше трудоемкости рассмотренных выше методов.
Существуют и некоторые другие методы подбора оптимального уравнения регрессии.
Общим недостатком всех рассмотренных ранее методов является использование для оценки модели того же экспериментального материала, на основе которого эта модель построена.
4) Иной подход основан на использовании регуляризации. При этом подходе все экспериментальные данные разбиваются на две части: обучающую (n 1) и проверочную (n 2). Первая из них используется для определения коэффициентов регрессии модели, вторая – для оценки модели в целом.
Оптимальные по этому подходу модели мало чувствительны к небольшим изменениям исходных данных.
Число точек обучающей последовательности должно быть, по крайней мере, на единицу больше числа коэффициентов регрессии (n 1 > m +1). Для повышения достоверности результатов этот запас должен быть существенно увеличен (n 1 ³ (2…3) m). Проверочная последовательность должна включать в себя хотя бы одну точку.
В ряде случаев в качестве критерия регуляризации удобно использовать критерий несмещенности, обеспечивающий наименьшее изменение модели при изменении состава обучающей последовательности. При этом весь экспериментальный массив разбивается на две одинаковые по величине последовательности (n 1 = n 2), каждая из которых поочередно используется в качестве обучающей. В результате их использования определяются две независимые, одинаковые по форме модели  и
и  . Оптимальная модель ищется по всем точкам выборки:
. Оптимальная модель ищется по всем точкам выборки:
Критерий регуляризации всегда имеет четко выраженный минимум, что обеспечивает объективное выделение модели оптимальной сложности.
3.6. Использование критерия Фишера для проверки значимости
высших степеней математической модели
Критерий Фишера может быть использован для сравнения точности двух (или нескольких) конкурирующих моделей.
Пусть рассматриваются две модели изучаемой системы (w1, w2), приводящие к двум различным множествам значений функции отклика: Wm 1, Wm 2.
Будем считать, что модель w2 более подробна и предположительно более точна, чем w1. Для каждой из моделей может быть составлена остаточная сумма квадратов:

и подсчитаны средние квадраты этих сумм (выборочные дисперсии):
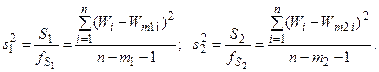
Для сравнения моделей подсчитывается так называемая дополнительная сумма квадратов SS, связанная с дополнительными данными, введенными в модель w2 , и характеризующаяся внесенными в нее уточнениями; а также число степеней свободы этой дополнительной суммы квадратов:
SS = S 1 – S 2; fSS = fS 1 – fS 2 = m 2 – m 1.
Средний квадрат дополнительной суммы определяется соотношением
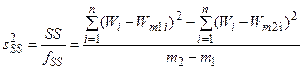 .
.
Если известна дисперсия экспериментальных данных s2(W), то роль дополнительной информации, содержащейся в модели w2, оценивается путем сравнения F -отношения с пороговым (критическим) значением критерия Фишера:
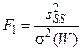 .
.
Если дисперсия экспериментальных данных s2(W) неизвестна, сравнение проводится с оценкой дисперсии для упрощенной модели  :
:
 .
.
Если полученное значение критерия Фишера значимо:
 или
или  ,
,
то дополнительная информация, заложенная в модели w2, существенна, и модель w2 действительно отличается от модели w1. В противном случае уточнения, вносимые моделью w2, неразличимы на фоне шума; с точки зрения точности модели равноценны, и предпочтение должно быть отдано более простой модели w1.
В частном случае полиномиальных моделей, представляющих собой конечные отрезки бесконечных рядов, этим методом можно проверить целесообразность включения в модель членов рада с более высокими степенями.
Рассмотрим пример, приведенный в п. 3.2 (лекция 7) с построенной моделью в виде полинома второй степени. Проанализируем целесообразность использования для данной выборки кубической модели типа Wm= a 0 + a 1 x + a 2 x 2 + a 3 x 3.
В результате расчетов методом наименьших квадратов можно найти коэффициенты такой модели:
Wm = –0,878 + 4,98 x – 0,768 x 2 + 0,032 x 3.
Вычислим остаточную сумму квадратов:
 .
.
Напомним, что остаточная сумма квадратов для модели второго порядка имела значение S 2 = 4,393.
Дополнительная сумма квадратов
SS = S 2 – S 3 = 0,144; fSS = m 3 – m 2 = 4 – 3 = 1.
Средний квадрат дополнительной суммы
 .
.
Критерий Фишера
 .
.
По статистическим таблицам распределения определяем критическое (пороговое) значение критерия Фишера при количестве степеней свободы f = n – m 2 – 1 = 10 – 3 – 1 = 6 и уровне риска a = 0,05
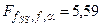 .
.
В связи с тем, что полученное из расчета значение критерия Фишера меньше критического, можно считать, что член третьего порядка не добавляет существенной информации и, следовательно, он является незначимым. Переход к модели третьего порядка нецелесообразен.
4.






