Классификация математических моделей
Существует несколько схем классификации математических моделей. Все они достаточно условны. Одна из таких схем приведена на рис. 1.3.
| Математические модели | ||||||||||
| Аналитические | Имитационные | |||||||||
| Теоретические | Эмпирические | Теоретические | ||||||||
| Линейные | Нелинейные | Нелинейные | ||||||||
| Статические | Динамические | Динамические | ||||||||
| Детермини-рованные | Стохастические | Детермини-рованные | ||||||||
| Аналитически разрешимые | Численно разрешимые | Численно разрешимые | ||||||||
Рис. 1.3
Все математические модели по использованному формальному языку можно разбить на аналитические и имитационные.
Аналитические – модели, в которых используется стандартный математический язык. Имитационные – модели, в которых использован специальный язык моделирования или универсальный язык программирования.
Аналитические модели могут быть записаны в виде формул или уравнений. Если какой-либо процесс не может быть описан в виде аналитической модели, его описывают с помощью специального алгоритма или программы. Такая модель является имитационной.
Аналитические модели в свою очередь разбиваются на теоретические и эмпирические модели. Теоретические модели отражают реальные структуры и процессы в исследуемых объектах, то есть, опираются на теорию их работы. Эмпирические модели строятся на основе изучения реакций объекта на изменение условий окружающей среды. При этом теория работы объекта не рассматривается, сам объект представляет собой так называемый «черный ящик», а модель – некоторую интерполяционную зависимость. Эмпирические модели могут быть построены на основе экспериментальных данных. Эти данные получают непосредственно на исследуемых объектах или с помощью их физических моделей.
По форме описания аналитические модели подразделяются на линейные и нелинейные.
Если все входящие в модель величины не зависят от времени, то имеем статическую модель объекта или процесса, в противном случае получаем динамическую модель.
В детерминированных моделях все взаимосвязи, переменные и константы заданы точно, что приводит к однозначному определению результирующей функции. Если часть или все параметры, входящие в модель по своей природе являются случайными величинами или случайными функциями, то модель относят к классу стохастических моделей.
В стохастических моделях задаются законы распределения случайных величин, что приводит к вероятностной оценке результирующей функции.
Если аналитическое исследование может быть доведено до конца, модели называются аналитически разрешимыми. В противном случае говорят о численно разрешимых аналитических моделях.
Геометрическое представление математических моделей
Геометрически математическая модель может быть представлена как некоторая поверхность отклика, соответствующая расположению точек W = W(x) в k-мерном факторном пространстве Х.
Наглядно можно представить себе только одномерную и двухмерную поверхности отклика, причем в последнем случае удобно пользоваться топографическим способом изображения рельефа поверхности с помощью линий уровня (изолиний), построенных в двумерном факторном пространстве Х. (Рис. 1.4).
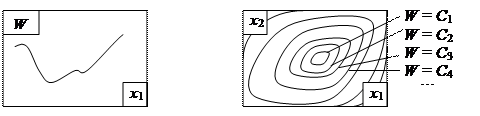 |
Рис. 1.4
Область, в которой определена поверхность отклика, называется областью определения Х*.
Эта область составляет, как правило, лишь часть полного факторного пространства Х (Х* Ì Х) и выделяется с помощью ограничений, наложенных на управляющие переменные xi, записанных в виде равенств
xi = Ci, i = 1,…, m;
fj (x) = Cj, j = 1,…, l
или неравенств
xi min £ xi £ xi max, i = 1,…, k;
fj (x) £ Cj, j = 1,…, n,
При этом функции fj (x) могут зависеть как одновременно от всех переменных, так и от некоторой их части.
Ограничения типа неравенств характеризуют или физические ограничения на процессы в изучаемом объекте (например, ограничения температуры), или технические ограничения, связанные с условиями работы объекта (например, предельная скорость резания).
Возможности исследования моделей существенно зависят от свойств (рельефа) поверхности отклика, в частности, от количества имеющихся на ней «вершин» и ее контрастности.
Количество вершин (впадин) определяет модальность поверхности отклика.
Если в области определения на поверхности отклика имеется одна вершина (впадина), модель называется унимодальной.
Характер изменения функции при этом может быть различным (Рис. 1.5).
| W | 
| W | W | ||
| x* x | x* x | x* x |
а б в
Рис. 1.5
Модель может иметь разрывы первого рода (см. рис. 1.5. а). Непрерывная унимодальная модель может иметь точки разрыва производной – разрывы второго рода (см. рис. 1.5. б). На рис. 1.5 в показана непрерывно-дифференцируемая унимодальная модель.
Для всех трех случаев, представленных на рис. 1.5, выполняется общее требование унимодальности:
Если W(x*) = extr W, то из условия х1 < x2 < x* (x1 > x2 > x*) следует
W(x1) < W(x2) < W(x*), если extr – максимум, или W(x1) > W(x2) > W(x*), если extr – минимум, то есть, по мере удаления от экстремальной точки значение функции W(x) непрерывно падает (растет).
Наряду с унимодальными бывают полимодальные модели (Рис. 1.6).
 |
| W | x 2 | X 1* X 2* | ||
| x 1* x 2* x 3* x | x 1 |
Рис. 1.6
Другим важным свойством поверхности отклика является ее контрастность, показывающая чувствительность результирующей функции к изменению факторов. Контрастность характеризуется величинами производных. Продемонстрируем характеристики контрастности на примере двумерной поверхности отклика (Рис. 1.7). Точка а расположена на «склоне», характеризующем равную контрастность по всем переменным хi (i =1,2); точка b расположена в «овраге», в котором различная контрастность по различным переменным (имеем плохую обусловленность функции); точка с расположена на «плато», на котором низкая контрастность по всем переменным хi говорит о близости экстремума.







