Универсальный горизонтальный питатель [88] рис. 1.21 состоит из рамы в виде направляющих 6 и 9, которые соединены между собой планками 2, 19. Рама установлена на оси 4 и прикреплена к кронштейну 12, в котором регулируется угол наклона. Отсекатель 7 с отверстиями под заготовки 21 движется в направляющих 6, 9. Отсекатель 7 через штифт 1 приводится в движение штоком 8 пневмоцилиндра 5. К планке 19 жёстко закреплены кулачки 18 и упор 16. Кулачки 18 взаимодействуют с двухплечевыми собачками 15, оси которых расположены в отверстиях отсекателя 7. Рычаги собачек 15 связаны между собой пружиной 20.

Рис. 1.21.
Питатель включает в себя магазин, нижняя часть которого выполнена в виде подвижной кассеты 3, установленной на подшипниках 10 в направляющих 6 и 9. Каретка состоит из стенок 11, соединённых между собой планками. Верхняя часть магазина состоит из съёмной кассеты 3.
К направляющим 6 и 9 прикреплён приёмник 17 с отверстиями под выпадаемые заготовки, к которому прикреплён приёмный лоток 14.
Питатель работает следующим образом. В исходном положении шток 8 пневмоцилиндра 5 отведён в крайнее левое положение. При этом двухплечевая собачка 15 упирается в первые выступы пазов стенок 11 магазина и препятствует его перемещению по направляющим 6, 9. Положение двухплечевой собачки 15 фиксируется таким образом, чтобы оси первых и вторых пазов кассеты 3 совпали с осями отверстий на отсекателе 7. Заготовки проваливаются в отверстия отсекателя и ложатся на поверхность приёмника 17.
При движении штока 8 пневмоцилиндра 5 вправо отсекатель 7 перемещается, а двухплечевые собачки 15 находят на кулачки 18 и разворачиваются к центру отсекателя, позволяя каретке магазина перемещаться под действием собственного веса по направляющим 6 и 9. Однако первая нижняя заготовка 21, упираясь в упор 16, стопорит движение магазина. При этом шток 8 занимает крайнее правое положение, а отверстия отсекателя 7 и приёмника 17 совмещаются. Из каждого отверстия отсекателя выпадает в приёмник и далее в лотки 14 по одной заготовке. Подаётся команда и шток занимает исходное положение.
Цикл повторяется до тех пор, пока последняя заготовка из первого пазамагазина не выпадет в отсекатель. После этого при очередном перемещении штока 8 в правое положение двухплечевые собачки 15 развернутся к центру отсекателя 7 и каретка магазина переместится по направляющим 6 и 9 до тех пор, пока заготовка из следующего паза не дойдёт до упора 16, предотвращая дальнейшее перемещение магазина.
Время срабатывания питателя равно сумме времён выполнения отдельных движений:
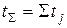 . (1.122)
. (1.122)
1й этап движения. Выпадение заготовки в отсекатель.
По аналогии с (1.86) время выпадания запишется:
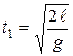 . (1.123)
. (1.123)
2й этап движения. Перемещение отсекателя для выдачи заготовки в приёмник и возвращение его в исходное положение согласно рис. 1.21 показано на рис. 1.22.

Рис. 1.22.
Этап 2а. Перемещение отсекателя для выдачи заготовки.
Учитывая, что в качестве привода используется пневмоцилиндр, найдём предельную скорость движения поршня, штока и отсекателя, при которой удар в шарнире А рис.1.23 будет вызывать упругие деформации на поверхностях штифта и втулки.
Воспользуемся теоремой об изменении главного вектора количества движения системы в интегральной форме [13].
 , (1.124)
, (1.124)
где  - векторы количества движения системы в конце и начале дви-
- векторы количества движения системы в конце и начале дви-
жения; 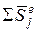 - главный вектор импульса внешних сил (
- главный вектор импульса внешних сил ( ).
).

Рис. 1.23.
Рассмотрим случай удара и запишем уравнение (1.124) в проекции на ось, направленную по движению системы:
 ,
,
где  - масса системы;
- масса системы;  - конечная и начальная скорость системы при ударе;
- конечная и начальная скорость системы при ударе;  - сила удара штифта о втулку;
- сила удара штифта о втулку;  - время удара.
- время удара.
Учитывая, что в конце удара скорость системы равна нулю, то последнее выражение запишется:
 . (1.125)
. (1.125)
Воспользуемся выражением работы, считая, что работы силы удара и силы при медленном сжатии (сдавливании) цилиндра (штифта) во внутреннюю цилиндрическую поверхность (втулку) при одинаковой деформации равны:
 , (1.126)
, (1.126)
где  - величина деформации штифта и втулки при ударе;
- величина деформации штифта и втулки при ударе;  - сила вдавливания цилиндра (штифта) во внутреннюю цилиндрическую поверхность (втулку);
- сила вдавливания цилиндра (штифта) во внутреннюю цилиндрическую поверхность (втулку);  - величина упругой деформации штифта и втулки.
- величина упругой деформации штифта и втулки.
Найдём составляющие выражения (1.126). Считая, что при ударе процесс упругого сжатия происходит равнозамедленно, имеем:

 . (1.127)
. (1.127)
Из теории прочности [54] имеем
 , (1.128)
, (1.128)
где  - допустимое напряжение на сжатие материалов штифта и втулки;
- допустимое напряжение на сжатие материалов штифта и втулки;  - площадь сжатия.
- площадь сжатия.
Согласно [25] полуось сжатия рис. 1.24 запишется:
 , (1.129)
, (1.129)
где  - нагрузка на единицу длины полосы контакта сжимаемых (сдавливаемых) тел;
- нагрузка на единицу длины полосы контакта сжимаемых (сдавливаемых) тел;  - соответственно, радиусы втулки и штифта;
- соответственно, радиусы втулки и штифта;  - модули упругости материалов штифта и втулки.
- модули упругости материалов штифта и втулки.
Из [25] нагрузка на единицу длины полосы контакта сдавливаемых тел:
 ,
,
где  - сила сдавливания тел (
- сила сдавливания тел ( );
); 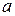 - длина полосы контакта согласно рис. 1.23
- длина полосы контакта согласно рис. 1.23  .
.

Рис. 1.24.
С учётом (1.128) последнее выражение запишется:
 . (1.130)
. (1.130)
Полоса контакта или площадь сжатия равна:
 . (1.131)
. (1.131)
Подставляем в (1.129) значение  (1.130),
(1.130),  (1.131), возводим в квадрат и после преобразований получим:
(1.131), возводим в квадрат и после преобразований получим:
 . (1.132)
. (1.132)
Из рис. 1.24 найдём величину деформации:
 . (1.133)
. (1.133)
Подставим составляющие (1.127, 1.128, 1.130, 1.133) в выражение (1.126), получим:  .
.
Из последнего выражения выделим правую часть уравнения (1.125), подставим в него это выражение и найдём предельную скорость движения системы, при которой при ударе возникнут только упругие деформации в штифте и втулке:
 . (1.134)
. (1.134)
Значение полуоси находится из выражения (1.132).
Пример 1.2. Найти предельную скорость движения отсекателя, при которой при ударе возникают упругие деформации в штифте и втулке.
Данные для расчёта приведены в таблице 1.2.
Таблица 1.2.
| Материал стержня сталь 45 | Радиус втулки | Радиус штифта | Длина взаимодействия штифта и втулки | Масса отсекателя | |
| Предел прочности на сжатие | Модуль упругости материала | ||||
 (кг/см2)
(кг/см2)
|  (кг/см2)
(кг/см2)
|  (см)
(см)
|  (см)
(см)
|  (см)
(см)
|  кг×с2/см
кг×с2/см
|
| 2×106 | 0,31 | 0,30 | 0,5 | 0,0081 |
Определяем скорость движения отсекателя:
 =23,37 см/с,
=23,37 см/с,
где  =2,58 × 10-3 см.
=2,58 × 10-3 см.
Определение жёсткости пружины пневмоцилиндра
Для обеспечения требуемой (1.134) скорости движения системы в пневмоцилиндре на его штоке рис. 1.22 необходимо поставить пружину торможения.
Найдём жёсткость этой пружины.
Воспользуемся принципом Даламбера [13].
Расчётная схема представлена на рис. 1.25.

Рис. 1.25.
Запишем выражение проекций сил на ось  .
.
 . (1.135)
. (1.135)
Сила пневмоцилиндра находится из выражения (1.104).
Сила инерции запишется:
 ,
,
где  - суммарная масса подвижных элементов системы;
- суммарная масса подвижных элементов системы;  - тангенциальное ускорение.
- тангенциальное ускорение.
Считая процесс торможения равнозамедленным движением, имеем:
 ,
,
где  - ход пневмоцилиндра (
- ход пневмоцилиндра (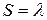 );
);  - берётся согласно выражения (1.134);
- берётся согласно выражения (1.134);  - время движения.
- время движения.
Сила пружины запишется:
 ,
,
где  - жёсткость пружины.
- жёсткость пружины.
Сила трения подвижных элементов системы:
 ,
,
где  - суммарный вес подвижных элементов системы;
- суммарный вес подвижных элементов системы;  - коэффициент трения.
- коэффициент трения.
Сила трения заготовок об отсекатель:
 ,
,
где  - число магазинов;
- число магазинов;  - число заготовок в магазине;
- число заготовок в магазине;  - вес заготовки.
- вес заготовки.
Подставляя в выражение (1.135) составляющие силы и после преобразований получим жёсткость пружины пневмоцилиндра.
 , (1.136)
, (1.136)
где  - ускорение свободного падения.
- ускорение свободного падения.
Учитывая, что сила пружины противостоит силе пневмоцилиндра, следовательно система может возвращаться в исходное положение под её действием.
 .
.
Определение величины сечения дросселя для управления скоростью
движения поршня пневмоцилиндра
Управлять скоростью движения поршня можно при помощи пружины, поставленной в полость пневмоцилиндра, а можно путём установки дросселя на входной штуцер.
Найдём сечения дросселя, при котором будет обеспечена требуемая скорость движения поршня.
Воспользуемся основным уравнением движения [13].
 .
.
Схема устройства представлена на рис. 1.22, а расчётная схема взаимодействия сил при движении приведена на рис. 1.26.
В проекции на ось  уравнение запишется:
уравнение запишется:
 , (1.137)
, (1.137)
где  - сила воздействия на поршень полости цилиндра, в которую подаётся давление;
- сила воздействия на поршень полости цилиндра, в которую подаётся давление;  - сила противодействия движению поршня от воздействия давления в противоположной полости;
- сила противодействия движению поршня от воздействия давления в противоположной полости; 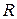 - сила вязкого трения.
- сила вязкого трения.

Рис. 1.26.
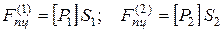 ,
,
где  - давление воздуха в полостях пневмоцилиндра;
- давление воздуха в полостях пневмоцилиндра;  - площади воздействия давления.
- площади воздействия давления.
Площадь воздействия давления в бесштоковой полости цилиндра равна:
 ,
,
где  - диаметр поршня.
- диаметр поршня.
Площадь в штоковой полости:
 ,
,
где  - диаметр штока.
- диаметр штока.
Подставляя составляющие члены в уравнение (1.137), получим:
 .
.
Быстрота нарастания давления в полости, в которую подаётся воздух через дроссель, описывается выражением:
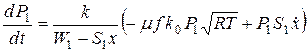 , (1.138)
, (1.138)
где  - коэффициент адиабаты;
- коэффициент адиабаты; 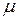 - коэффициент расхода газа (
- коэффициент расхода газа (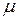 =0,9);
=0,9);  - площадь сечения дросселя;
- площадь сечения дросселя;  - постоянный коэффициент;
- постоянный коэффициент; 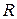 - газовая постоянная;
- газовая постоянная;  - температура газа по Кельвину;
- температура газа по Кельвину;  - объём полости цилиндра, в которую подают газ;
- объём полости цилиндра, в которую подают газ;  - скорость перемещения поршня, которая находится из (1.134).
- скорость перемещения поршня, которая находится из (1.134).
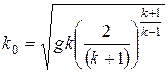 . (1.139)
. (1.139)
При установившемся движении из уравнения (1.138) имеем:
 .
.
Отсюда площадь се6чения дросселя, при которой будет обеспечена требуемая скорость равна:
 . (1.140)
. (1.140)
Определение времени срабатывания отсекателя при выдаче заготовки
Воспользуемся основным уравнением динамики [13].
Расчётная схема показана на рис. 1.27.

Рис. 1.27.
Спроектируем уравнение на ось  .
.
 , (1.141)
, (1.141)
где  (
( берётся из (1.140));
берётся из (1.140));  - сила вязкого трения;
- сила вязкого трения; 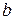 - коэффициент вязкого трения.
- коэффициент вязкого трения.
Подставим составляющие части в (1.141) и преобразуем уравнение.

Обозначим в уравнении: коэффициент при  -
-  ; коэффициент при
; коэффициент при  -
-  ; постоянный член правой части уравнения А, получим:
; постоянный член правой части уравнения А, получим:
 .
.
Решение данного уравнения аналогично решению уравнения (1.119).
Время срабатывания отсекателя соответствует перемещению 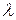 .
.
Определение времени возвращения отсекателя в исходное положение
В исходном положении отсекатель возвращается под действием пружины.
Воспользуемся основным уравнением динамики [13].
Расчётная схема приведена на рис. 1.28.

Рис. 1.28.
В проекции на ось  имеем:
имеем:
 ,
,
где  .
.
После подстановки составляющих уравнения и преобразования получим:
 .
.
По аналогии с предыдущим введём обозначения.
Дифференциальное уравнение запишется:
 .
.
Решение данного уравнения ищем по аналогии с уравнением (1.119).
Находим время возвращения отсекателя в исходное положение при перемещении на величину 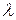 .
.






