Бункерные загрузочные устройства с возвратно-поступательным движением стержня

Бункерное загрузочное устройство с возвратно-поступательным движением стержня [16] рис. 1.9.

Устройство предназначено для поштучной ориентированной выдачи заготовок типа трубок, колпачков, стаканчиков. Заготовки засыпают в чашу 1 с конусообразным дном навалом. Через отверстие во втулке 2, расположенной на дне чаши, проходит стержень 3, совершающий возвратно-поступательное движение. Проходя через толщу заготовок, стержень их ворошит и одна из заготовок, ориентируясь, надевается на конец стержня. Стержень, выдвигаясь вверх, подаёт заготовку в приёмный лоток (трубку) 6, снабжённый запорными собачками, исключающими при обратном движении стержня выпадание заготовки из него. Стержень связан с толкателем 4 через пружину 5, предохраняющую механизм от поломок в случаях переполнения приёмного лотка заготовками.

 

 

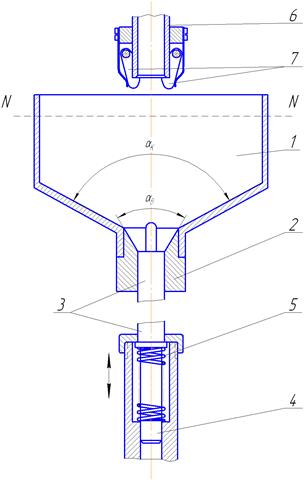
Рис. 1.9.

 

Для исключения заклинивания заготовок при движении стержня выбирают угол конуса чаши в пределах 110…130°, а угол конуса втулки =80…100°.

Найдём предельную скорость движения стержня, при которой при ударе его о заготовку на её поверхности возникнут только упругие деформации.

Воспользуемся выражением работы, считая, что работы силы удара стержня о заготовку и силы медленного вдавливания стержня в заготовку при одинаковой деформации равны.

Тогда , (1.30)

где - сила удара; - деформация заготовки при ударе; - сила сжатия заготовки; - деформация заготовки при сжатии.

Учитывая, что заготовка не закреплена, то можно утверждать, что в первом приближении сила удара равна силе инерции в момент начала движения заготовки.

, (1.31)

где - коэффициент, учитывающий взаимодействие заготовок между собой в момент начала движения ударяемой заготовки ( = 1,3…2,5); - масса заготовки; - тангенциальное ускорение в момент начала движения ударяемой заготовки.

Считаем, что при упругой деформации заготовки от удара стержнем имеем дело с равнозамедленным движением:

; . (1.32) окончательно, (1.33)

где - путь, пройденный стержнем при ударе, равный деформации заготовки; - время удара; - начальная скорость деформации в момент удара.

Величина деформации заготовки равна:

, (1.34)

где - средняя скорость деформации ; - скорость деформации в конце удара .

Работа силы удара с учётом (1.31, 1.33 и 1.34) запишется:

.

Учитывая, что , окончательно получим:

. (1.35)

Из теории прочности на сжатие имеем:

.

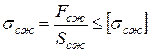Отсюда , (1.36)

где - напряжение и допустимое напряжение материала заготовки на сжатие; - площадь сжатия.

Наконечник стержня имеет форму сферы радиусом 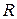. Согласно формуле Герца [25] величина упругой деформации плоскости заготовки при взаимодействии со сферической поверхностью при одинаковых материалах равна:

, (1.37)

где - сила сдавливания деталей; - модули упругости материалов.

Из [25] выражение полуоси, т.е. радиуса пятна упругой деформации при одинаковых материалах плоскости и сферы запишется:

. (1.38)

Сила сдавливания равна (1.36)

. (1.39)

Площадь сжатия равна:

. (1.40)

Подставим (1.39, 1.40) в (1.38) и после преобразований найдём :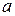

. (1.41)

Подставим (1.39, 1.40 и 1.41) в (1.37) и после преобразований получим:

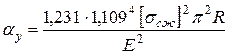. (1.42)

Подставим (1.39, 1.40 и 1.37) в выражение (1.30) и после преобразований найдём предельную скорость движения стержня:

. (1.43)

Подставим в последнее выражение (1.41 и 1.42) окончательно получим предельную скорость движения стержня, при которой при ударе о заготовку на её поверхности возникнут только упругие деформации.

Производительность выдачи заготовок бункерными загрузочными устройствами с возвратно-поступательным движением стержня находится из выражения: ,

где - число двойных ходов стержня в минуту; - коэффициент вероятности захвата заготовок ( =0,2…0,4).

,

где - ход толкателя (мм).

В случае если сфера стержня и заготовка будут изготовлены из различных материалов, то:

;

,

где ,

где - коэффициент Пуассона ( =0,3).