
 Это уравнение векторное и в проекциях на оси выбранной системы координат дает три уравнения. Вывод дифференциального уравнения движения в общем случае требует громоздких математических выкладок. Поэтому для упрощения вывода рассмотрим одномерное течение жидкости. Выделим в потоке вязкой жидкости, как показано на рис. 2.3, элементарный объем с размерами ребер dx, dy и dz.
Это уравнение векторное и в проекциях на оси выбранной системы координат дает три уравнения. Вывод дифференциального уравнения движения в общем случае требует громоздких математических выкладок. Поэтому для упрощения вывода рассмотрим одномерное течение жидкости. Выделим в потоке вязкой жидкости, как показано на рис. 2.3, элементарный объем с размерами ребер dx, dy и dz.
 |
Рис. 2.3
Скорость в потоке изменяется только в направлении оси Оу. Силы, действующие на элемент жидкости, можно разделить на массовые (или объемные) и поверхностные. К массовым силам относятся сила тяжести, центробежная сила и электромагнитные силы. Мы в дальнейшем будем учитывать только силу тяжести. К поверхностным силам относятся силы давления и силы трения. Найдем проекции этих сил на ось Ох.
Сила тяжести равна произведению массы элемента на проекцию ускорения свободного падения на ось Ох

Равнодействующая сил давления в проекции на ось Ох равна

Равнодействующая сил трения с учетом уравнения (1.11) в проекции на ось Ох составляет

Суммируя  получим проекцию равнодействующей всех сил на ось Ох, приложенных к объему
получим проекцию равнодействующей всех сил на ось Ох, приложенных к объему
 (а)
(а)
Согласно второму закону механики эта равнодействующая равна произведению массы элемента на проекцию ее ускорения на ось Ох и учитывает силы инерции
 (б)
(б)
Приравнивая правые части (а) и (б) и производя сокращения, получим уравнение движения вдоль оси Ох

В общем случае трехмерного движения несжимаемой жидкости уравнение движения в проекциях на оси Ox, Oy и Oz соответственно имеет вид:
 (2.5)
(2.5)
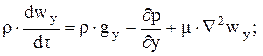 (2.6)
(2.6)
 (2.7)
(2.7)
Или в векторном виде
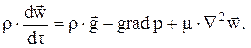 (2.8)
(2.8)
Уравнения (2.5) – (2.8) называют уравнениями Навье-Стокса. Член, стоящий в левой части уравнений, представляет собой полную производную от скорости по времени
 (2.9)
(2.9)
где i соответственно x, y, z.
Первые слагаемые в правой части (2.9) характеризуют локальное изменение скорости во времени в какой-либо точке жидкости. Остальные три слагаемых в правой части характеризуют изменение скорости при переходе от точки к точке. Такая полная производная называется субстанциональной производной. Уравнения движения получены при постоянных теплофизических свойствах жидкости. В то же время свободное движение жидкости (естественная конвекция) определяется разностью плотностей холодных и нагретых частиц жидкости. В общем случае при r¹const необходимо учитывать и энергию деформации жидкости. Поэтому ограничимся приближенным учетом переменности плотности в слагаемом, связанным с силой тяжести в уравнениях движения. Пусть плотность линейно зависит от температуры

где r и r0 – плотности, соответствующие температурам t и t0;
J=t-t0; t0 – некоторая фиксированная температура (точка отсчета).
Подставляя это значение плотности в первое слагаемое правой части (2.8), получим приближенно

Первое слагаемое правой части  можно трактовать как сумму силы тяжести
можно трактовать как сумму силы тяжести 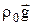 , взятой при определенной плотности, и подъемной (архимедовой) силы
, взятой при определенной плотности, и подъемной (архимедовой) силы  . Член
. Член 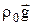 можно представить как градиент гидростатического давления р0 в покоящейся жидкости с плотностью r0. Тогда вместо
можно представить как градиент гидростатического давления р0 в покоящейся жидкости с плотностью r0. Тогда вместо  можно написать grad p1, где p1=p-p0. При такой замене приближенное векторное уравнение движения будет описывать и естественное движение жидкости (естественную конвекцию)
можно написать grad p1, где p1=p-p0. При такой замене приближенное векторное уравнение движения будет описывать и естественное движение жидкости (естественную конвекцию)
 (2.10)
(2.10)
Таким образом, для задач теплообмена система дифференциальных уравнений сохранения массы (уравнение неразрывности или сплошности), энергии и движения в проекциях на координатные оси оказывается замкнутой. Эта система уравнений в принципе позволяет определить в движущейся жидкости поле температуры T=T(x, y, z, t), поле давлений p=p(x, y, z, t) и поля проекций скоростей wx=wx(x, y, z, t), wy=wy(x, y, z, t), wz=wz(x, y, z, t).
Для задач массообмена, не осложненных теплообменом (в изотермических условиях), уравнение энергии в этой системе заменяется уравнением сохранения массы i-го компонента смеси. Вывод этого уравнения, которое называют уравнением массообмена, аналогичен выводу дифференциального уравнения сохранения энергии при qV=0 и имеет вид
 (2.11)
(2.11)
где mi=Ci/r – относительная массовая концентрация i-го компонента.
В случаях, когда массообмен осложнен теплообменом (в неизотермических условиях), кроме уравнения (2.11), необходимо уравнение сохранения энергии. Однако вывод этого уравнения с учетом (1.13) усложняется. Для двух компонентной (бинарной) смеси оно имеет вид


 (2.12)
(2.12)
Из этого уравнения видно, что, если удельные изобарные теплоемкости компонентов смеси равны ср1=ср2, то результирующий перенос энтальпии отсутствует, и это уравнение переходит в ранее полученное уравнение (2.4).






