Эти законы можно выразить общей формулировкой: плотность потока любой субстанции, переносимой микроскопическим способом, прямо пропорциональна градиенту соответствующего потенциала.
По закону Фурье плотность потока тепла, переносимого теплопровод-ностью, прямо пропорциональна градиенту температуры
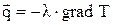, (1.9)
где l – коэффициент теплопроводности, вт/м×град.
Знак минус в правой части равенства необходим, так как вектора градиент температуры и плотность теплового потока лежат на одной прямой, если l скалярная величина, но направлены в разные стороны. Коэффициент теплопроводности изменяется для известных материалов в диапазоне от 10-3до102 вт/м×град. Вещества, у которых l<0,25 вт/м×град, называют теплоизоляторами. У анизотропных тел коэффициент теплопроводности по разным направлениям оказывается разным, в отличие от изотропных тел, и вектора плотности потока тепла и градиента температуры не лежат на одной прямой. В общем случае коэффициент теплопроводности зависит от темпера-туры. У чистых металлов (кроме алюминия) с ростом температуры коэффи-циент теплопроводности уменьшается. У газов, наоборот, возрастает. Для большинства капельных жидкостей, исключая воду в диапазоне температур от 0 до 150оС, с ростом температуры коэффициент теплопроводности умень-шается. Чем больше компонентов входит в смесь, тем меньше ее коэффициент теплопроводности. В отличие от теплоемкости смеси, коэффициент ее теплопроводности не обладает свойством суммируемости (аддитивности) в соответствии, например, с массовыми долями компонентов, входящими в смесь. Для влажного материала коэффициент теплопроводности выше, чем коэффициент теплопроводности сухого материала и воды. По закону Фика плотность потока массы отдельного компонента смеси, переносимого молекулярной диффузией, прямо пропорциональна градиенту концентрации этого компонента
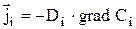, (1.10)
где Di – коэффициент диффузии i-того компонента смеси, м2/с.
Для обычных газовых смесей при атмосферном давлении коэффициенты диффузии имеют значения от 0,1×10-4 до 10-4 м2/с и уменьшаются с увеличением давления смеси. У капельных жидкостей коэффициенты диффузии меньше, чем у газов, и имеют значения от 0,5×10-4 до 2×10-9 м2/с. В отличие от газов, коэффициенты диффузии в жидкостях часто существенно изменяются с концентрацией. Коэффициенты диффузии в твердых телах изменяются в диапазоне от 10-6 до 2×10-14 м2/с. С ростом температуры коэффициенты диффузии увеличиваются.
По закону Ома плотность электрического тока прямо пропорциональна градиенту электрического потенциала
,
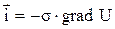где s – коэффициент электропроводности, Ом-1×м-1.
Для различных материалов коэффициент электропроводности изменяется в диапазоне от 6×107 до10-16 Ом-1×м-1.
По закону Ньютона плотность потока количества движения, переносимого микроскопическим способом, прямо пропорциональна градиенту скорости
,
где m – коэффициент динамической вязкости, н×сек/м2.
Плотность потока количества движения в общем случае трехмерного движения – тензорная величина, поэтому рассмотрим более простое одномерное поле скоростей течения жидкости
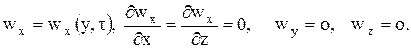
Тогда по закону Ньютона касательное напряжение трения (или плотность потока количества движения, переносимого микроскопическим способом) прямо пропорционально градиенту скорости
. (1.11)
Таким образом, причиной внутреннего трения при движении вязкой жидкости является перенос количества движения микрочастицами в неоднородном поле скоростей. Даже при малом коэффициенте динамической вязкости m, например у газов, в случае больших градиентов скорости силы вязкого трения будут значительными. У капельных жидкостей коэффициент динамической вязкости резко уменьшается с ростом температуры, а у газов несколько возрастает.
Необходимо отметить, что перечисленные выше законы переноса различных субстанций, в отличие от законов сохранения самих субстанций, например энергии, могут нарушаться при очень больших градиентах соответствующих потенциалов. В чистом виде эти законы выполняются при неоднородности тех потенциалов, которые входят в соответствующий закон. При этом другие потенциалы в изучаемой области однородны.
Если, например, в неподвижной двухкомпонентной смеси имеют место неоднородности концентраций i-го компонента, неоднородности температуры и давления, то наряду с концентрационной диффузией, описываемой законом Фика, возникнут термическая диффузия (эффект Соре) и бародиффузия. Суммарная плотность потока массы i-го компонента смеси с учетом концентрационной диффузии, термо- и бародиффузии составит
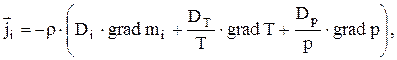(1.12)
где r – плотность смеси;
mi = Ci /r – относительная массовая концентрация i-того компонента;
DT = KTDi – коэффициент термодиффузии;
Dp = KpDi – коэффициент бародиффузии;
p – давление смеси;
KT, Kp – коэффициенты.
Доля массы i-го компонента в общем потоке, переносимого термодиффузией, незначительна, и только при больших градиентах температур ощущается ее влияние. Бародиффузия проявляется при значительных перепадах давления. В процессах теплообмена такие случаи встречаются редко.
Аналогично при микроскопическом способе переноса тепла в смеси, когда не однородны температура, концентрация компонентов смеси и давление, суммарная плотность потока тепла с учетом теплопроводности, определяемой законом Фурье, диффузионной теплопроводностью (эффект Дюфо) и переноса тепловой энергии за счет диффузии составит
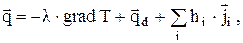(1.13)
где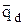 
– плотность потока диффузионной теплопроводности;
hi – удельная энтальпия i-го компонента смеси;
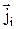– суммарная плотность потока массы i-го компонента смеси.
Диффузионная теплопроводность для многокомпонентной смеси исследована мало; кроме того, ее величина в общем потоке незначительна, поэтому ею часто пренебрегают. Последнее слагаемое в правой части (1.13), связанное с переносом энтальпии в результате диффузии, обычно мало, и его следует учитывать при высоких температурах в случаях существенной диссоциации газов. Поля потенциалов, в частности, поле скоростей жидкости, определяются из дифференциальных уравнений сохранения субстанций.
