При низких температурах и высоких давлениях поведение газов существенно отличается от поведения идеальных газов. Реальные газы при температурах ниже критической 
, в результате сжатия, переходят в жидкое состояние. Одно из уравнений, приближенно описывающих состояние реальных газов, – это уравнение Ван-дер-Ваальса
,
- поправка, учитывающая силы притяжения молекул, 
-поправка, учитывающая собственный объем молекул, 
-число молей газа, 
-газовая постоянная, 
-давление газа, 
-объем сосуда, занимаемого газом.
Поправки и связаны с критической температурой , критическим давлением 
и критическим объемом 
,
= 
, = 
, = 
.
ЖИДКОСТИ. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ.
Сила 
поверхностного натяжения, препятствующая разрыву поверхности жидкости, пропорциональна длине 
участка контура, ограничивающего эту поверхность,
, (35)
и направлена по касательной к ней. 
- коэффициент поверхностного натяжения.
Добавочное давление на искривленную поверхность жидкости, обусловленное силами поверхностного натяжения, описывается формулой Лапласа
, (36)
и 
- радиусы кривизны двух взаимно перпендикулярных сечений поверхности жидкости. Если центр кривизны находится внутри жидкости, радиус кривизны положителен, вне жидкости – отрицателен. Для сферической поверхности = = ,
. (37)
Работа, необходимая для увеличения поверхности жидкости на величину 
, численно равна приращению энергии 
ее поверхностного слоя
= ∙ .
ТВЕРДЫЕ ТЕЛА.
Деформация растяжения стержня. Закон Гука.
При малых деформациях растяжения (сжатия) стержня выполняется закон Гука
, (38)
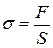- механическое напряжение, - растягивающая (сжимающая) сила, 
- площадь поперечного сечения стержня;
- относительное удлинение (сжатие) стержня, - изменение длины 
стержня;
-модуль Юнга (коэффициент, характеризующий упругие свойства материала стержня).
Тепловое расширение твердых тел.
При повышении температуры на 
изменение длины тела в первом приближении пропорционально 
, (39)
-температурный коэффициент линейного расширения материала, - длина тела при температуре 
.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ.
1. Трофимова Т.И. Курс физики. М.:Академия, 2008.-560 c.
2. Детлаф А.А., Яворский Б.М. Курс физики. М.:Высш.шк., 1999.-718 с.
3. Зисман Г.А., Тодес О.М. Курс общей физики. М.:Наука. 1969. т.1-3.
4. Яворский Б.М., Детлаф А.А. Справочник по физике. М.:Наука. 1985.-512с.
5. Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. М.:Наука. 1988.-256 с.
6. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями. М.:Высш.шк., 2002.-591 c.
